http://zh.wikipedia.org/wiki/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E9%93%BE
马尔可夫链,因安德烈·马尔可夫得名,是数学中具有马尔可夫性质的离散时间随机过程。该过程中,在给定当前知识或信息的情况下,只有当前的状态用来预测将来, 过去(即当前以前的历史状态)对于预测将来(即当前以后的未来状态)是无关的。
马尔可夫链是随机变量X1,X2,X3...的一个数列。这些变量的范围,即他们所有可能取值的集合,被称为“状态空间”,而Xn的值则是在时间n的状态。如果Xn + 1对于过去状态的条件概率分布仅是Xn的一个函数,则
这里x为过程中的某个状态。上面这个恒等式可以被看作是马尔可夫性质。
性质
马尔可夫链是由一个条件分布来表示的
这被称为是随机过程中的“转移概率”。这有时也被称作是“一步转移概率”。二、三,以及更多步的转移概率可以导自一步转移概率和马尔可夫性质:
同样,
这些式子可以通过乘以转移概率并求k − 1次积分来一般化到任意的将来时间n + k。
边际分布 P(Xn)是在时间为n时的状态的分布。初始分布为P(X0)。该过程的变化可以用以下的一个时间步幅来描述:
这是Frobenius-Perron equation的一个版本。这时可能存在一个或多个状态分布π满足
其中Y只是为了便于对变量积分的一个名义。这样的分布π被称作是“平稳分布”(Stationary Distribution)或者“稳态分布”(Steady-state Distribution)。一个平稳分布是一个对应于特征根为1的条件分布函数的特征方程。
平稳分布是否存在,以及如果存在是否唯一,这是由过程的特定性质决定的。“不可约”是指每一个状态都可来自任意的其它状态。当存在至少一个状态经过一个固定的时间段后连续返回,则这个过程被称为是“周期的”。
离散状态空间中的马尔可夫链
如果状态空间是有限的,则转移概率分布可以表示为一个具有(i,j)元素的矩阵,称之为“转移矩阵”:
对于一个离散状态空间,k步转移概率的积分即为求和,可以对转移矩阵求k次幂来求得。就是说,如果 是一步转移矩阵,
是一步转移矩阵,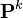 就是k步转移后的转移矩阵。
就是k步转移后的转移矩阵。
平稳分布是一个满足以下方程的向量
-
 .
.
在此情况下,稳态分布π * 是一个对应于特征根为1的、该转移矩阵的特征向量。
如果转移矩阵 不可约,并且是非周期的,则
不可约,并且是非周期的,则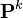 收敛到一个每一列都是不同的平稳分布 π * ,并且,
收敛到一个每一列都是不同的平稳分布 π * ,并且,
-
 ,
,
独立于初始分布π。这是由Perron-Frobenius theorem所指出的。
正的转移矩阵(即矩阵的每一个元素都是正的)是不可约和非周期的。矩阵被称为是一个随机矩阵,当且仅当这是某个马尔可夫链中转移概率的矩阵。
注意:在上面的定式化中,元素(i,j)是由j转移到i的概率。有时候一个由元素(i,j)给出的等价的定式化等于由i转移到j的概率。在此情况下,转移矩阵仅是这里所给出的转移矩阵的转置。另外,一个系统的平稳分布是由该转移矩阵的左特征向量给出的,而不是右特征向量。
转移概率独立于过去的特殊况为熟知的Bernoulli scheme。仅有两个可能状态的Bernoulli scheme被熟知为贝努利过程












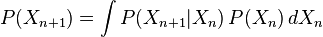


















 2218
2218

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








