详细的问题和题解可查看网易公开课提供的课件下载。
1. 使用用牛顿法计算最小平方
我们希望证明:当使用牛顿法解决最小平方优化问题时,只需一步即可迭代至最优解
解:
(1)计算损失函数J(θ)的Hessian矩阵
已知损失函数表达式为
则其一阶导数为
二阶导数为
因此J(θ)的Hessian矩阵为 H=X^T*X
(2)计算一次迭代后的结果
这与最优解θ*是一致的,得证。
2. 局部加权Logistic回归
由于没有找到训练和测试的数据,本题不再详解。
3. 多元最小平方
在之前的课程中,我们一致认为分类/回归的结果y是一个标量,现在我们将其推广至一个p维的向量
解:
(1)








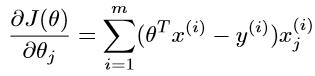


 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2550
2550

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








