【最优化】拉格朗日乘子法

拉格朗日乘子法

前面几节讲述的都是无约束优化问题的相关算法，但是在实际生活中碰到的几乎都是有约束问题模型。

等式约束的拉格朗日乘子法

算法框架

1. 问题描述

以下对约束优化问题中常出现的概念做一下简要解释：

• 可行解：所有满足约束条件的向量
• 不可行解：至少有一个约束条件不满足的向量
• 最优解：在可行域中使得目标函数趋于最优的解向量

2. 求解思路

核心：把一个有约束问题转换成一个无约束优化问题。

原问题（如上图）是一个含有m个约束条件，n维的有约束优化问题；通过在目标函数中增加拉格朗日乘子，将其转换成一个问题维数为n+m但是无约束的优化问题（如下图）。

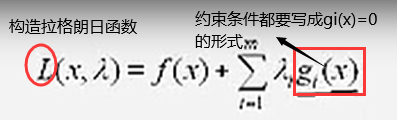
3. 无约束优化问题的必要条件方程

• Tip 1：因为上述是必要条件，所以只有当函数L(x,λ)的最优解存在的情况下，方程才成立；
• Tip 2：f(x)的最优解存在并不意味着对应的无约束优化目标函数L(x,λ)的最优解存在。

4. 示例

【Tips】

• 如果某些约束条件可以化成显函数的形式（即某一个变量用其余变量进行表示），那么可以把该变量用其余变量进行代入，从而达到消除问题维度和减少约束条件数目的作用。

例如：

• 一般地，加上约束的目标函数优化问题得到的最优解不会比无约束优化问题的最优解更好，因为约束条件只是对可行域进行限制。

拉格朗日乘数λ的存在性

就像我们前面一直在强调的，即使原问题存在最优解，也并不意味着构造出来的拉格朗日函数具有最优解。

1. 结论：如果约束条件向量在候选最优点的偏导矩阵是行满秩矩阵，那么该候选最优点才是最优点。

2. 示例

---

不等式约束的拉格朗日乘子法

1. 问题描述

其中问题给出的形式都是“≥”符号，是因为如果形如【g(x)≤0】的不等式约束可以改写成【-g(x)≥0】的形式。

2. 求解思路

核心：把一个不等式约束问题转换成一个等式约束问题来求解，引入松弛变量。

对于每一个不等式约束条件h_i(x)，都定义一个相应的实数型松弛变量θ_i，故可定义出θ_i ²=h_i(x) ，则将原式中的m个不等式约束条件等价转换成形如【θ_i ²=h_i(x)】这样的等式约束条件。
构造出来的拉格朗日函数如下：

3. 必要条件方程

• case 1：λ_i=0，θ_i≠0，相当于是一个无约束优化问题，因为所有的约束条件h_i(x) = θ_i²都因为λ_i=0而不影响最优点的取舍。从图形的观点来看，就是限制域本身就包含了原问题的可行域。
• case 2：λ_i≠0，θ_i=0，相当于是一个标准的等式约束优化问题，不等式约束因为θ_i=0变为纯等式约束，而因为λ_i≠0，所以最优点的梯度并不是0。从图形的观点来看，就是在限制域的边界上取得问题的最优解。
• case 3：λ_i=0，θ_i=0，限制域的边界穿过了原问题的最优解。因此虽然这个问题转换成了等式约束的优化问题，但是依然可以按照原问题的最优点条件求得极值点。
  
  4. 示例
  

---

不等式约束问题的KT条件

在前面求解不等式约束问题的时候，我们通过引入一个松弛变量，把不等式约束问题进行转换；但这样会引入很多新的变量，使得问题的计算与求解变得更复杂。
于是我们提出了KT条件——分析不等式约束问题的最优解应该满足的若干条件。

最小化约束问题的KT条件

后续会分析，其实最小化到最大化问题之间的变换只有符号的处理不太相同，这里分类进行整理也方便读者查阅结论进行记忆。

1. 问题描述

2. KT条件陈述
（1）标量形式

（2）矩阵向量形式

3. KT条件的性质

• 【必要性】KT条件是不等式约束问题最优解存在的必要条件，即当x是最优解的情况下，在x处一定满足这个条件
• 【充分必要性】如果目标函数和不等式约束多项式f(x)和g(x)都是凸函数的情况下，KT条件就成为了最优解存在的充分必要条件。

4. 示例

最大化约束问题的KT条件

针对最大化约束问题，按照不同的处理方式可以得到两种KT条件的表述形式；因此在应用KT条件求解最大化不等式约束问题的时候，首先要把类拉格朗日函数写出来。

因为KT条件的形式和类拉格朗日函数的形式是相互对应的。

1. max f(x)与min -f(x)问题是相互等价的

2. 利用最大最小化等价之后，对λ整体进行代换

按照上面思路1的方式，得到的KT条件的第一项是个等式约束（形如下图）。等式两边同时乘上(-1)，则再把原来的λ_i系数用(-λ_i)来替换，就能得到新的KT条件约束。

3. 示例