1 决策树算法概述
-
树模型是一种基于树形结构的机器学习模型,决策树是其中的典型代表;
-
决策树的结构与决策过程:
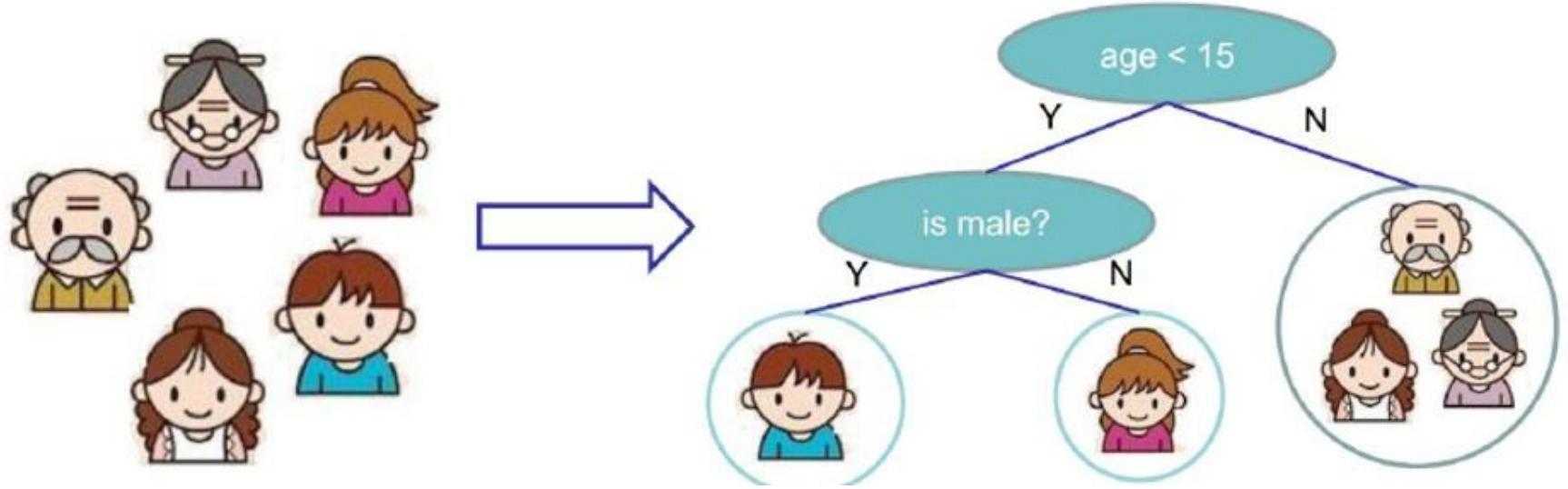
- 决策树由根节点、非叶子节点与分支、叶子节点组成;
- 从根节点开始,数据根据不同特征的条件判断,沿着相应分支逐步向下,最终到达叶子节点;
- 在这个过程中,每一步的判断都基于数据的某个特征值,直至到达叶子节点得到最终决策结果;
- 比如在判断是否适合出门打球的决策树中,根节点可能是天气特征,根据天气是晴天、阴天还是雨天,数据被分到不同分支,继续后续判断,直到叶子节点给出是否打球的决策;
-
决策树的应用:
- 决策树既可以用于分类任务,也能用于回归任务;
- 在分类任务中,叶子节点的决策结果是不同的类别,例如判断邮件是垃圾邮件还是正常邮件;
- 在回归任务中,叶子节点的输出是一个连续的数值,比如预测房屋的价格;
- 这是因为决策树能够对数据的特征进行有效分析和划分,挖掘数据中的潜在规律,所以能在不同类型的任务中发挥作用;
-
决策树的基本组成结构:

- 根节点:是决策树的第一个选择点,是数据进入决策树进行分类或回归判断的起始点,图中“Outlook”节点就是根节点;
- 非叶子节点与分支:
- 代表决策过程中的中间步骤;
- 非叶子节点基于特定特征进行条件判断,分支则是根据判断结果引导数据走向不同路径;
- 比如“Humidity”“Wind”节点是非叶子节点,从它们出发的连线就是分支;
- 叶子节点:
- 表示最终的决策结果;
- 到达叶子节点的数据就得到了最终分类或回归的判定结论,如“Overcast”“High”“Normal”“Weak”“Strong”等节点;
- 图中节点旁标注的类似“9 / 5”的数字,可能代表不同类别的样本数量分布等相关统计信息,用于辅助理解节点划分数据的情况。
-
决策树的特征切分(节点选择):
- 问题:在构建决策树时,根节点以及后续节点该选用哪个特征?如何对特征进行切分?
- 比喻:
- 我们的目标应该是根节点就像一个老大似的能更好的切分数据(分类的效果更好),其在数据切分中应起到关键作用,要能使分类效果更好;
- 根节点下的节点如同“二当家”,辅助进一步划分数据;
- 解决:要通过特定衡量标准,计算不同特征用于分支选择后的分类情况,从中挑选出最能有效划分数据的特征作为根节点,后续节点也按此方式依次确定,以此构建决策树。
2 熵的作用
-
决策树中用于特征切分的衡量标准——熵;
-
熵的定义:
- 熵用于度量随机变量的不确定性,通俗来讲就是反映物体内部的混乱程度;
- 如杂货市场物品繁杂,混乱度高;专卖店只售单一品牌,稳定性强;
-
熵的公式: H ( X ) = − ∑ i = 1 n p i ∗ l o g p i H(X)=-\sum_{i = 1}^{n}p_{i}*logp_{i} H(X)=−∑i=1npi∗logpi ,其中 p i p_{i} pi 是随机变量 X X X 取值为第 i i i 个状态的概率,通过该公式可计算熵值;
-
示例:
- 给出A集合 [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 2 , 2 ] [1,1,1,1,1,1,1,1,2,2] [1,1,1,1,1,1,1,1,2,2] 和B集合 [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 1 ] [1,2,3,4,5,6,7,8,9,1] [1,2,3,4,5,6,7,8,9,1];
- A集合类别少,相对稳定,熵值低;B集合类别多,混乱度高,熵值大;
- 在决策树分类任务中,期望通过节点分支后数据类别的熵值变小,即数据更有序、更易分类。
3 信息增益原理
-
熵与不确定性关系:
-
不确定性越大,熵值越大;
-
当随机变量取值概率 p = 0 p = 0 p=0 或 p = 1 p = 1 p=1 时, H ( p ) = 0 H(p)=0 H(p)=0 ,意味着随机变量完全确定;
-
当 p = 0.5 p = 0.5 p=0.5时, H ( p ) = 1 H(p)=1 H(p)=1 ,此时随机变量不确定性达到最大;
-
下图展示了熵值 H ( X ) H(X) H(X) 随概率 P r ( X = 1 ) Pr(X = 1) Pr(X=1) 变化的趋势,呈现先升后降的曲线形态;

-
-
如何选择决策树节点的呢?
-
信息增益:
- 信息增益用于衡量特征 X X X 使类 Y Y Y 不确定性减少的程度,追求分类后同类聚集,即分类结果具有专一性;
- 在决策树构建中,倾向选择信息增益大的特征作为节点,以有效降低数据不确定性,提升分类效果。
4 决策树构造实例
-
数据与目标
outlook temperature humidity windy play sunny hot high FALSE no. sunny hot high TRUE no. overcast hot high FALSE yes rainy mild high FALSE yes rainy cool normal FALSE yes rainy cool normal TRUE no. overcast cool normal TRUE yes sunny mild high FALSE no. sunny cool normal FALSE yes rainy mild normal FALSE yes sunny mild normal TRUE yes overcast mild high TRUE yes overcast hot normal FALSE yes rainy mild high TRUE no. 
-
数据:基于14天的打球情况数据,包含outlook(天气)、temperature(温度)、humidity(湿度)、windy(是否有风)这4种环境变化特征,以及对应的是否打球(play)结果;
-
目标:构造决策树,核心问题是确定哪个特征作为根节点;
-
-
计算原理 - 信息增益
- 信息增益用于衡量特征使类的不确定性减少的程度,通过计算不同特征划分数据后的熵值变化来确定;
- 熵是表示随机变量不确定性的度量 ,公式为
H
(
X
)
=
−
∑
i
=
1
n
p
i
∗
l
o
g
p
i
H(X)=-\sum_{i = 1}^{n}p_{i}*logp_{i}
H(X)=−∑i=1npi∗logpi ,通过该公式可计算熵值;
- 公式中 p i p_{i} pi 是随机变量 X X X 取值为第 i i i 个状态的概率;
- 信息增益越大,说明该特征对分类的贡献越大;
-
计算过程
-
初始熵值计算:
-
14天数据中,9天打球,5天不打球;
-
根据熵的计算公式 H ( X ) = − ∑ i = 1 n p i log 2 p i H(X)=-\sum_{i = 1}^{n}p_{i}\log_{2}p_{i} H(X)=−∑i=1npilog2pi,这里 n = 2 n = 2 n=2(打球和不打球两种情况), p 1 = 9 14 p_1=\frac{9}{14} p1=149(打球的概率), p 2 = 5 14 p_2=\frac{5}{14} p2=145(不打球的概率);
-
计算过程如下:
H ( X ) = − 9 14 log 2 9 14 − 5 14 log 2 5 14 = − 9 14 ( log 2 9 − log 2 14 ) − 5 14 ( log 2 5 − log 2 14 ) = − 9 14 log 2 9 + 9 14 log 2 14 − 5 14 log 2 5 + 5 14 log 2 14 = − 9 14 log 2 9 − 5 14 log 2 5 + ( 9 14 + 5 14 ) log 2 14 = − 9 14 log 2 9 − 5 14 log 2 5 + log 2 14 ≈ − 9 14 × 3.17 − 5 14 × 2.32 + 3.81 ≈ − 2.03 − 0.83 + 3.81 = 0.940 \begin{align*} H(X)&=-\frac{9}{14}\log_{2}\frac{9}{14}-\frac{5}{14}\log_{2}\frac{5}{14}\\ &=-\frac{9}{14}(\log_{2}9 - \log_{2}14)-\frac{5}{14}(\log_{2}5 - \log_{2}14)\\ &=-\frac{9}{14}\log_{2}9+\frac{9}{14}\log_{2}14-\frac{5}{14}\log_{2}5+\frac{5}{14}\log_{2}14\\ &=-\frac{9}{14}\log_{2}9-\frac{5}{14}\log_{2}5 + (\frac{9}{14}+\frac{5}{14})\log_{2}14\\ &=-\frac{9}{14}\log_{2}9-\frac{5}{14}\log_{2}5 + \log_{2}14\\ &\approx - \frac{9}{14}\times3.17 - \frac{5}{14}\times2.32+3.81\\ &\approx -2.03 - 0.83 + 3.81\\ &= 0.940 \end{align*} H(X)=−149log2149−145log2145=−149(log29−log214)−145(log25−log214)=−149log29+149log214−145log25+145log214=−149log29−145log25+(149+145)log214=−149log29−145log25+log214≈−149×3.17−145×2.32+3.81≈−2.03−0.83+3.81=0.940
-
-
以outlook特征为例计算:
-
outlook取值为sunny时,熵值为0.971;取值为overcast时,熵值为0;取值为rainy时,熵值为0.971 ;
-
其取值为sunny、overcast、rainy的概率分别为 5 14 \frac{5}{14} 145、 4 14 \frac{4}{14} 144、 5 14 \frac{5}{14} 145;
-
加权计算熵值为 5 / 14 ∗ 0.971 + 4 / 14 ∗ 0 + 5 / 14 ∗ 0.971 = 0.693 5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693 5/14∗0.971+4/14∗0+5/14∗0.971=0.693 ;
-
根据加权熵计算公式 H ( X ) = ∑ i = 1 n p i H ( X i ) H(X)=\sum_{i = 1}^{n}p_{i}H(X_i) H(X)=∑i=1npiH(Xi)( p i p_i pi是第 i i i种取值的概率, H ( X i ) H(X_i) H(Xi)是第 i i i种取值下的熵值)
H ( X ) = 5 14 × 0.971 + 4 14 × 0 + 5 14 × 0.971 = 5 14 × 0.971 × 2 = 10 14 × 0.971 ≈ 0.693 \begin{align*} H(X)&=\frac{5}{14}\times0.971+\frac{4}{14}\times0+\frac{5}{14}\times0.971\\ &=\frac{5}{14}\times0.971\times2\\ &=\frac{10}{14}\times0.971\\ &\approx0.693 \end{align*} H(X)=145×0.971+144×0+145×0.971=145×0.971×2=1410×0.971≈0.693 -
信息增益计算:信息增益 G a i n = Gain = Gain=初始熵值 - 加权熵值,即 0.940 − 0.693 = 0.247 0.940 - 0.693 = 0.247 0.940−0.693=0.247
-
-
其他特征信息增益:同样方式计算出temperature信息增益为0.029,humidity信息增益为0.152,windy信息增益为0.048;
-
-
节点确定
- 比较各特征信息增益,选择信息增益最大的特征作为根节点;
- 这里outlook特征信息增益最大,所以优先选outlook作为根节点,后续再以类似方式在其余特征中确定下一级节点,逐步构建完整决策树。
5 三种常见的决策树算法及衡量标准
-
ID3算法
-
衡量标准:信息增益,即特征X使得类Y的不确定性减少的程度;
-
问题:倾向于选择取值较多的特征,因为取值多的特征可能使数据划分得更细,信息增益更大。但这样可能导致过拟合,而且对缺失值较为敏感;
-
-
C4.5算法
-
衡量标准:信息增益率。在信息增益的基础上,除以特征自身的熵(称为分裂信息)进行归一化;
-
作用:解决了ID3倾向于选择取值多的特征的问题,对特征取值数量进行了约束,能更好地处理连续值和缺失值;
-
-
CART算法
-
衡量标准:GINI系数,公式为 G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p)=\sum_{k = 1}^{K}p_{k}(1 - p_{k}) = 1-\sum_{k = 1}^{K}p_{k}^{2} Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kpk2 ,其中 p k p_{k} pk是样本属于第 k k k类的概率;
-
特点:和熵类似,用于衡量数据集的不纯度,值越小表示数据集纯度越高,可用于分类和回归任务 ,构建的决策树是二叉树。
-
6 处理连续值的方法
- 问题提出:在决策树构建时,当遇到连续值特征,需要确定选取哪个分界点来对数据进行划分;
- 解决算法:采用贪婪算法;
- 具体步骤
- 排序:将连续值特征的取值按从小到大顺序排列,如“60 70 75 85 90 95 100 120 125 220” 。
- 确定分界点:
- 对排序后的值进行“二分”尝试划分,可能产生多个分界点(示例中10个值有9个可能分界点);
- 像以80为分界点,可将数据分割成TaxIn≤80和TaxIn>80两部分;
- 以97.5为分界点,可分割成TaxIn≤97.5和TaxIn>97.5两部分;
- 这一过程本质是将连续值离散化,以便在决策树中像处理离散值特征一样进行节点划分。
7 决策树剪枝策略
-
为什么要剪枝:
- 决策树在训练过程中,如果不加以限制,可能会过度拟合训练数据;
- 这是因为从理论上讲,决策树可以不断细分,直至每个叶子节点只对应一个数据实例;
- 这样的树在训练集上表现极好,但面对新的测试数据时,泛化能力很差,预测效果不佳;
- 所以需要通过剪枝策略来降低过拟合风险,提升模型泛化能力;
-
预剪枝:
- 操作方式:
- 在决策树构建过程中,边生长边判断是否进行剪枝;
- 例如,在一个节点准备进行分裂时,先基于一些条件(如限制深度、限制叶子节点个数、限制叶子节点样本数、限制信息增益量等)评估分裂后是否能提升模型在验证集上的性能;
- 限制深度:设定决策树的最大层数,当树达到该深度时,不再继续分裂节点;
- 限制叶子节点个数:控制叶子节点的数量上限,达到上限后不再分裂;
- 限制叶子节点样本数:规定叶子节点中最少的样本数量,若样本数过少则不再分裂;
- 限制信息增益量:当特征分裂带来的信息增益小于一定阈值时,停止分裂;
- 如果不能提升甚至可能导致性能下降,就停止该节点的进一步分裂,直接将其作为叶子节点;
- 优点:计算开销小,因为不需要完整构建整棵树,能提前终止一些不必要的分支生长,节省训练时间和资源,实用性较高;
- 缺点:有欠拟合风险,因为过早停止节点分裂,可能错过一些能提升模型性能的潜在划分;
- 操作方式:
-
后剪枝:
- 操作方式:
- 先完整构建一棵决策树,然后从叶子节点开始,自下而上地对每个节点进行评估;
- 通过一定的衡量标准
C
α
(
T
)
=
C
(
T
)
+
α
⋅
∣
T
l
e
a
f
∣
C_{\alpha}(T)=C(T)+\alpha\cdot|T_{leaf}|
Cα(T)=C(T)+α⋅∣Tleaf∣ ,判断剪掉该节点及其子树是否能提升模型在验证集上的性能,如果能则进行剪枝操作;
- 其中 C ( T ) C(T) C(T)是模型在训练集上的误差, ∣ T l e a f ∣ |T_{leaf}| ∣Tleaf∣是叶子节点数量 , α \alpha α是权衡参数;
- 该公式表明叶子节点越多, C α ( T ) C_{\alpha}(T) Cα(T)值越大,损失越大;
- 优点:能更准确地判断哪些节点应该被剪掉,因为是基于完整的树结构进行评估,一般能有效提升模型泛化能力;
- 缺点:计算开销大,需要先构建完整的树,再进行大量的剪枝评估操作,训练时间较长;
- 操作方式:
-
例:下面是一棵基于CART算法构建的决策树

-
节点信息
-
条件判断:每个非叶子节点都包含一个条件判断,例如“X[2]<=2.45” ,表示根据特征X的第2个维度的值与2.45比较进行分支。这里的X是特征向量,不同的X[i]代表不同的特征维度。
-
GINI系数:用于衡量节点的不纯度,GINI系数取值范围在0 - 1之间,值越小表示节点数据纯度越高,即类别越单一 。如根节点gini = 0.6666,说明初始时数据混合程度较高;而一些叶子节点gini = 0,表示该节点数据类别完全一致 。
-
样本数量(samples):表示该节点包含的样本总数。例如根节点samples = 149,意味着最初有149个样本在这个节点参与划分 。
-
类别分布(value):以数组形式展示各类别样本数量。如根节点value = [49, 50, 50] ,表示在149个样本中,分别属于三个类别的样本数为49、50、50 。
-
-
分支情况:从根节点开始,根据条件判断结果分为True和False两个分支。例如根节点“X[2]<=2.45” ,满足该条件的样本进入True分支,不满足的进入False分支。每个分支又会基于新的节点条件继续划分,直至到达叶子节点;
-
叶子节点:叶子节点不再进行划分,其GINI系数为0时表示该节点内样本属于同一类别 。叶子节点的类别分布明确了该节点中各类别样本的数量情况,可据此确定样本的最终分类归属 。 这棵决策树通过不断对特征进行划分,将初始的样本集逐步细分,以实现对样本的分类预测。
-

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








