矩阵链乘
一.问题简述
给定n个矩阵{A 1 A 2 …A n },其中A i 和A i+1 是可乘的,这n个矩阵的连乘积A 1 A 2 …A n 。由于矩阵的乘法满足结合律,故计算矩阵的连乘积有许多不同的计算次序,而不同的计算次序,所需要计算的连乘次数也是不同的,求解连乘次数最少的矩阵连乘最优次序。
输入一个序列P={p0,p1,….pn},矩阵A的维数为pi-1*pi。
假设有三个矩阵A1、A2、A3,三个矩阵的维数分别为10*100,100*5,5*50,则P={10,100,5,50}
二.算法分析
按照动态规划法处理问题的步骤:
(1)最优加括号的全部结构
动态规划方法的第一步是寻找最优子结构,然后,利用这一子结构,就可以根据子问题的最优解构造出一个原始问题的最优解。用记号Ai..j表示对乘积AiAi+1…Aj求值的结果;对Ai…Aj任何加括号的形式都将在Ak,与Ak+1之间分开。也就是说,对于某个k值,先计算Ai..k和Ak+1..j然后再把他们相乘,这样就得到最终乘积Ai…j。
(2)一个递归解
对于矩阵链乘问题,子问题就是确定AiAi+1…Aj的加全部括号的最小代价问题,1<=i<=j<=n,m[i,j]为计算矩阵Ai..j所需的标量乘法运算的最小值;对于整个问题,计算A1…n的最小代价就是m[1,n]。
(1)矩阵链只包含一个矩阵,即i=j时,m[i,i] = 0;
(2)i < j时,m[i,j]=m[i,k]+m[k+1,j]+pi-1*pk*pj
所以,最优值可以递归的定义为:
(3)计算最优代价
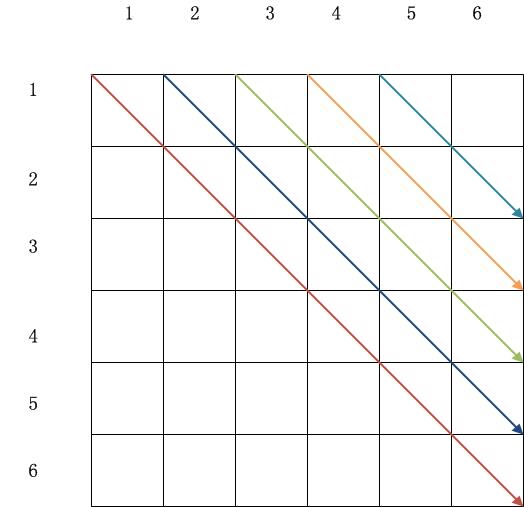
使用自底向上的表格法来求解最优代价,输入的是一个序列p={p0,p1,p2,…pn},表示有n个矩阵相乘A1的维数为p0*p1,A2的维数为p1*p2……以此类推,直到An…,m[1…n,1..n]来保存m[i,j]的代价,表s[1..n,1..n]来记录m[i,j]时取得最优代价k的值,即插入括号的位置。
代码实现:
#include <stdio.h>
#include <malloc.h>
#include <limits.h>
#define MAX 100
/*动态规划矩阵链乘*/
typedef struct
{
int m[MAX][MAX];
int s[MAX][MAX];
}res;
void InitP(int* p,int length)
{
int i;
printf("\n初始化序列p,请输入p的维数\n");
for (i=0;i<length;i++)
{
printf("p[%d]=",i);
scanf("%d",&p[i]);
}
}
res Matrix_Chain_Order(int* p,int length)
{
res count;
int n = length - 1;
int i,l,j,k,q;
for (i=1;i<=n;i++)
count.m[i][i] = 0;
for (l=2;l<=n;l++)
{
for (i=1;i<=(n-l+1);i++)
{
j=i+l-1;
count.m[i][j] = INT_MAX;
for (k=i;k<=j-1;k++)
{
q = count.m[i][k]+count.m[k+1][j]+p[i-1]*p[k]*p[j];
if (q < count.m[i][j])
{
count.m[i][j] = q;
count.s[i][j] = k;
}
}
}
}
return count;
}我们现在举例分析假设输入的序列P={30,35,15,5,10,20,25},表示6个矩阵:
| 矩阵 | 维数 |
|---|---|
| A1 | 30*35 |
| A2 | 35*15 |
| A3 | 15*5 |
| A4 | 5*10 |
| A5 | 10*20 |
| A6 | 20*25 |
n = length -1;即n=6,为矩阵的个数,中间程序是三层for循环嵌套,现在,我们分析程序执行的过程。(l为子问题的规模)
1.◆l=2;l<=n=6;l++(l为子问题的规模),一重for循环
●i=1;i<=n-l+1=5;(i为子问题前端点的范围),二重for循环
j=2=i+l-1;(j为子问题后端点的范围)
m[1,2]=m[i,j]=∞
★ k=i=1;K<=j-1=1;三重for循环
q=m[1,1]+m[2,2]+p0*p1*p2=0+0+15750=15750
if (q < count.m[i][j])即15750<∞为真
m[1,2]=15750;
s[1,2]=k=1;
返回到★处执行k=2时,不满足for循环,返回上一层for循环●处,执行i=2,j=3;因此,我们观察,当子问题规模为l=2时,有以下几种情况:
| 子问题规模为2,l=2 |
|---|
| m[1,2]=m[1,1]+m[2,2]+p0*p1*p2=0+0+15750=15750 s[1,2]=1 |
| m[2,3]=m[2,2]+m[3,3]=p1*p2*p3=2625 s[2,3]=2 |
| m[3,4]=m[3,3]+m[4,4]=p2*p3*p4=750 s[3,4]=3 |
| m[4,5]=m[4,4]+m[5,5]=p3*p4*p5=1000 s[4,5]=4 |
| m[5,6]=m[5,5]+m[6,6]=p4*p5*p6=5000 s[5,6]=5 |
2.l=3时,
| 子问题规模为3,l=3 |
|---|
| m[1,3]=min(m[1,1]+m[2,3]+p[0]*p[1]*p[3],m[1,2]+m[3,3]+p[0]*p[2]*p[3]); |
| m[2,4]=min(m[2,2]+m[3,4]+p[1]*p[2]*p[4],m[2,3]+m[4,4]+p[1]*p[3]*p[4]); |
| m[3,5]=min(m[3,3]+m[4,5]+p[2]*p[3]*p[5],m[3,4]+m[5,5]+p[2]*p[4]*p[5]) |
| m[4,6]=min(m[4,4]+m[5,6]+p[3]*p[4]*p[6],m[4,5]+m[6,6]+p[3]*p[5]*p[6]) |
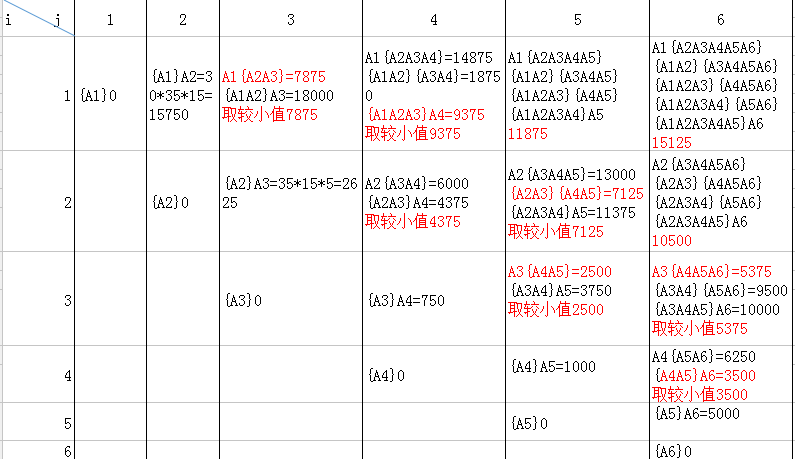
迭代执行该过程,直到l=6为止;
计算过程:
(4)构造最优解
即根据S[1…n,1…n]记录的数据打印出最优加括号的位置k
void Print_Optimal_Parens(int (*s)[MAX],int i,int j)
{
if (i==j)
{
printf("A%d",i);
}
else
{
printf("(");
Print_Optimal_Parens(s,i,s[i][j]);
Print_Optimal_Parens(s,s[i][j]+1,j);
printf(")");
}
}
main函数调用的格式:
printf("请输入下标i,j的值,即输出<Ai,...Aj>最优加全部括号的形式(i,j取值在1~%d之间)\n",length-1);
printf("i=");scanf("%d",&i);
printf("j=");scanf("%d",&j);
printf("<A%d,A%d,...A%d>最优加全部括号的形式\n",i,i+1,j);
Print_Optimal_Parens(count.s,i,j);
三.总结
执行结果:
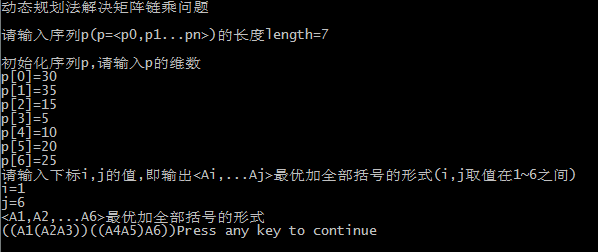
Matrix_Chain_Order三层嵌套,运行时间为O(n*n*n)
源代码下载地址:http://download.csdn.net/detail/koudan567/9513232
Reference:
(1)《算法导论》15.2矩阵链乘法
(2)http://www.tuicool.com/articles/67Nz6f2
(3)http://blog.csdn.net/tmljs1988/article/details/6925631







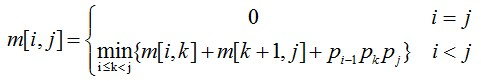














 667
667











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








