算法学习——动态规划（Python代码）

一、问题的提出

我们来看这样一个问题

• 你有三种硬币，分别面值2元、5元和7元，每种硬币都有足够多
• 买一本书需要27元
• 如何用最少的硬币组合起来正好付清，不需要对方找钱

我们直觉会怎么想？

你有三种硬币，分别面值2元、5元和7元，每种硬币都有足够多，买一本书需要27元，如何用最少的硬币组合起来正好付清，不需要对方找钱

• 最少的硬币组合➡尽量用面值大的硬币

√ 7+7+7+7=28

√ 7+7+7=21

√ 21+5=26

√ 这样显然拼不出来

• 改一下思路➡先用面值大的硬币,最后如果可以用一种硬币付清就行

√ 7+7+7=21

√ 21+2+2+2=27

√ 这次应该对了吧，其实正确答案是：7+5+5+5+5=27，5枚

所以我们需要更加科学的方法来计算这个问题

二、基本原理

1、基本概念

动态规划是运筹学的一个分支，通常用来解决多阶段决策过程最优化问题。动态规划的基本想法就是将原问题转换为一系列相互联系的子问题，然后通过逐层地推来求得最后的解。目前，动态规划常常出现在各类计算机算法竞赛或者程序员笔试面试中，在数学建模中出现的相对较少，但这个算法的思想在生活中非常实用，会对我们解决实际问题的思维方式有一定启发。

添加图片注释，不超过 140 字（可选）

2、基本步骤

一、 确定状态：解动态规划的时候需要开一个数组，数组的每个元素需要明确代表什么，类似于确定数学题中X、Y的含义

√ 最后一步 √ 子问题

二、转移方程：把状态表达成方程

三、初始条件和边界情况

四、 计算顺序

三、典型例题

1、问题

你有三种硬币，分别面值2元、5元和7元，每种硬币都有足够多，买一本书需要27元，如何用最少的硬币组合起来正好付清，不需要对方找钱

一、确定状态

最后一步：

• 虽然我们不知道最优策略是什么，但是最优策略肯定是有k枚硬币， 𝑎1,𝑎2,⋯𝑎𝑘 加起来面值为27

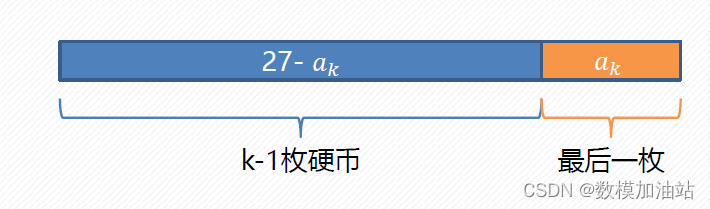
• 所以一定存在有最后一枚硬币： 𝑎𝑘

• 除了这枚硬币，前面硬币的面值加起来是 27−𝑎𝑘

（1）两个关键点

1）我们不关心前面的k-1枚硬币是怎么拼出 27−𝑎𝑘 的（可能有很多种拼法），而且我们现在甚至还不知道a_k和k是多少，但我们可以确定前面的硬币拼出了 27−𝑎𝑘

2）因为是最优策略，所以拼出 27−𝑎𝑘 的硬币数一定要最少，否则就不是最优策略

（2）子问题

最少用多少枚硬币可以拼出 27−𝑎𝑘

原问题是最少用多少枚硬币可以拼出27

我们将原问题可以转化成一个规模更小的子问题： 27−𝑎𝑘

• 状态：我们可以设状态f(x)=最少用多少枚硬币拼出x

2、递归解法

现在我们还不知道最后那枚硬币 𝑎𝑘 是多少，但它只能是2，5或7

• 如果 𝑎𝑘 =2，f(27)=f(27-2)+1

• 如果 𝑎𝑘 =5，f(27)=f(27-5)+1

• 如果 𝑎𝑘 =7，f(27)=f(27-7)+1

显然只有这三种可能

要求最小的硬币数，所以：

𝑓(27)=𝑚𝑖𝑛{𝑓(27−2)+1,𝑓(27−5)+1,𝑓(27−7)+1}

如果有学习过递归的，应该看得出来，这可以用递归来进行求解

递归python代码:

# 递归算法
def f(x):
    """
    递归函数，用于计算找零的最少硬币数。
    参数x：找零的金额
    返回值：最少硬币数量，如果无法找零，则返回无穷大
    """
    if x == 0:
        return 0  # 如果找零金额为 0，则不需要任何硬币，直接返回 0
    res = float('inf')  # 用一个很大的数表示无穷大，用于比较最小值
    if x >= 2:
        # 如果找零金额大于等于 2 元，尝试使用一枚 2 元硬币
        res = min(f(x - 2) + 1, res)  # 递归调用 f 函数，并加上这一枚硬币
    if x >= 5:
        # 如果找零金额大于等于 5 元，尝试使用一枚 5 元硬币
        res = min(f(x - 5) + 1, res)  # 递归调用 f 函数，并加上这一枚硬币
    if x >= 7:
        # 如果找零金额大于等于 7 元，尝试使用一枚 7 元硬币
        res = min(f(x - 7) + 1, res)  # 递归调用 f 函数，并加上这一枚硬币
    return res  # 返回最少硬币数量，如果无法找零，则返回无穷大
n=int(input('请输入要拼的金额：'))
res=f(n)
print(res)

3、动态规划解法

状态：我们可以设状态f[x] =最少用多少枚硬币拼出x

对于任意x

𝑓[𝑥]=𝑚𝑖𝑛⁡{𝑓[𝑥−2]+1,𝑓[𝑥−5]+1,𝑓[𝑥−7]+1}

转移方程有两个问题： x-2 , x-5 ,或x-7小于0怎么办？什么时候停下来？

• 如果不能拼出Y，那么就定义f[Y]=正无穷，例如f[-1]= f[-2]= f[-3]=⋯=正无穷

• 所以f[1]=min⁡{f[-1]+1 ,f[-4]+1 ,f[-6]+1}=正无穷，表示拼不出来

• 初始条件f[0]=0

计算顺序：

• 拼出x所需要的最少硬币数：f[x]=min⁡{f[x-2]+1 ,f[x-5]+1 ,f[x-7]+1}

• 初始条件f[0]=0

• 然后计算f[1] ,f[2] , ⋯, f[x]

• 这样当我们计算到f[x] 时， f[x-2] ,f[x-5] ,f[x-7]都已经算过了

• 每一步是算三次，算到27是第27步，故时间复杂度（需要的步数）为27×3（金额×硬币种数）

• 递归时间复杂度>> 27×3

4、典型例题——背包问题

有一个小偷去偷东西，他的背包可以容纳总重量为W的物品，现在有n件物品，每件物品的重量为，价值为 ，求能够放进背包的物品的最大价值。

状态：dp[i][j]表示前i件物品放入容量为j的背包中所获得的最大价值

状态转移方程：对于第i件物品，可以选择放或不放

• 如果不放，那么 𝑑𝑝[𝑖][𝑗]=𝑑𝑝[𝑖−1][𝑗]

• 如果放，那么 𝑑𝑝[𝑖][𝑗]=𝑑𝑝[𝑖−1][𝑗−𝑤_𝑖]+𝑣_𝑖

• 选择获得最大价值的情况，即

𝑑𝑝[𝑖][𝑗]=𝑚𝑎𝑥(𝑑𝑝[𝑖−1][𝑗],𝑑𝑝[𝑖−1][𝑗−𝑤_𝑖]+𝑣_𝑖)

初始条件：

• dp[0][0] = 0，将前 0 个物品放入容量为 0 的背包中能获得的最大价值为 0

• 如果容量为 0，则无法放入任何物品，dp[i][0] = 0

• 如果没有物品可选，则无法放入任何物品，dp[0][j] = 0。

求解顺序：从第一个物品开始，求解到n

最终，dp[n][w]即为问题的解

四、相关代码

1、凑硬币py代码

def coinChange(n):
    """
    用于计算找零的最少硬币数。
    参数n：要找零的金额
    返回值：最少硬币数量，如果无法找零，则返回-1
    """
    dp = [float('inf')] * (n + 1)  # 初始化动态规划数组
    dp[0] = 0  # 找零金额为 0 时，需要 0 枚硬币
    for i in range(1, n + 1):
        if i >= 2:
            dp[i] = min(dp[i], dp[i - 2] + 1)
        if i >= 5:
            dp[i] = min(dp[i], dp[i - 5] + 1)
        if i >= 7:
            dp[i] = min(dp[i], dp[i - 7] + 1)
    if dp[n] != float('inf'):
        return dp[n]
    else:
        return -1
n=int(input('请输入要拼的金额：'))
res=coinChange(n)
print(res)

2、背包问题py代码

def knapsack(weights, values, capacity):
    """
    用于求解0-1背包问题的最大价值
    参数weights：物品的重量列表
    参数values：物品的价值列表
    参数capacity：背包的容量
    返回值：最大价值
    """
    n = len(weights)  # 物品数量
    dp = [[0 for j in range(capacity + 1)] for i in range(n + 1)]  # 初始化动态规划数组

    # 动态规划求解过程
    for i in range(1, n + 1):
        for j in range(1, capacity + 1):
            if j < weights[i - 1]:  # 背包容量小于当前物品重量，不能选择当前物品
                dp[i][j] = dp[i - 1][j]
            else:  # 能选择当前物品，要选择价值更大的方案
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])
    return dp[n][capacity]
w = input('请输入物品的重量列表，用逗号分隔：')
v = input('请输入物品的价值列表，用逗号分隔：')
c = int(input('请输入背包的容量：'))
weights = [int(x) for x in w.split(',')]  # 将输入的字符串转换为整数列表
values = [int(x) for x in v.split(',')]
res = knapsack(weights, values, c)
print('最大价值为:', res)