20、python数据结构——动态规划

动态规划也是数据结构算法的一种思想。

我们来看看我们熟悉的斐波那契数列，F(n)=F(n-1) + F(n-2)，我们来写一下实现的递归和非递归版本。

def fibnacci(n):
    if n==1 or n==2:
        return 1
    else:
        return fibnacci(n-1) + fibnacci(n-2)
    
def fibnacci_no_recurision(n):
    f = [0,1,1]
    if n>2:
        for i in range(n-2):
            num = f[-1] + f[-2]
            f.append(num)
    return f[n]

print(fibnacci(30))
print(fibnacci_no_recurision(30))

在数值比较大的时候，我们会明显发现递归方法程序执行的时间变长了，这是为什么呢？其实是因为我们重复计算子结构的原因，因为我们在使用递归的时候，对每一个子问题是需要重复计算的，我们可以通过下图理解：

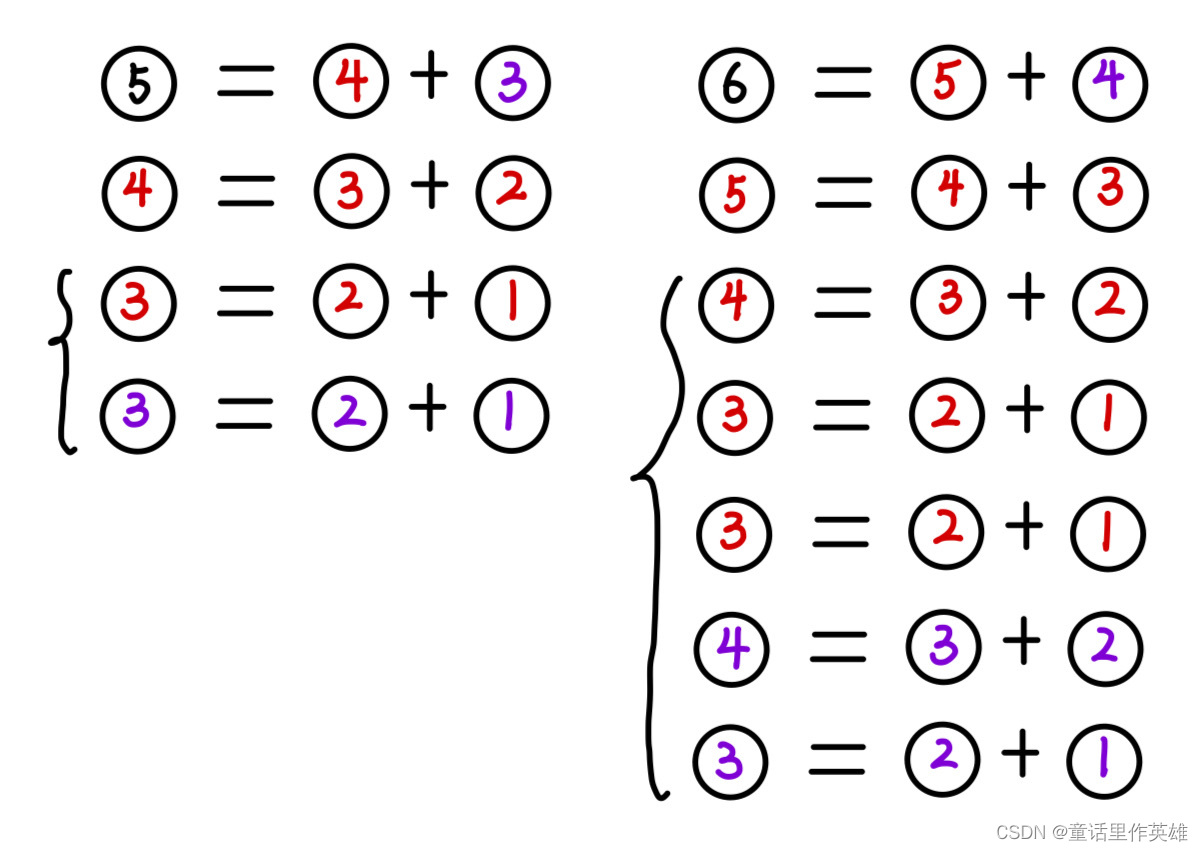
每个递归都是独立的，递归之中重复计算了很多相同的计算式，所以当数值越大，计算的时间也就越久，效率很低。
使用非递归的话，就可以解决这种重复递归的情况，我们把计算出来的值用列表存起来，这个时候就可以直接调用，无需重复计算。

这个时候就涉及到了动态规划中的最优子结构，最优子结构有两个步骤：1、找到一个递推式；2、重复子问题（解决方法：循环存起来）
斐波那契数列的解决思想其实就是包含了动态规划的思想。

应用

1、钢条切割问题：某公司出售钢条，出售价格和长度之间的关系如下：

长度i	1	2	3	4	5	6	7	8	9	10
价格pi	1	5	8	10	13	17	18	22	25	30

思路：1、找出递推式；2、重复子问题

其实对于钢条切割的话，有很多种切法，并且还有切多少刀的问题，如果长度是n的话，就有2^n-1种切法（每个位置有两种选择：切与不切，有n-1个位置），所以太过于复杂了，但是现在我们考虑只切一刀，从左往右切的话，就能简化这个问题，因为我们可以先从最短的开始，一步一步算出最长的切法，所以我们对任何一个进行切割，都不需要去看表，而是看我们自己设计的最优切法后对应长度最高价格的表，然后切一刀的左右两边都小于等于自身长度，又已知我们短的最优价格，即可得到切割最好的位置。

1、最直接的方式：
设置长度为n的钢条切割后最优收益值为r_n，可以得到递推式：
r_n = max（p_n，r₁+r_n-1，r₂+r_n-2，…，r_n-1+r_n）
第一个参数p_n表示不切割，其他n-1个参数表示另外n-1种不同的方案，对方案i = 1,…,n-1：将钢条切割为长度为i和n-i两段，方案i的收益为切割两段的最优收益之和。把所有方案一起比较，选择收益最大的那个。

递推式可以简化：r_n = max（p_i+r_n-i） (1 <= i <= n)
不切割的方案就可以描述为：左边一段长度为n，收益为p_n，剩余一段长度为0，收益为r₀。

p = [0,1,5,8,9,10,17,17,20,24,30]

def cut_rod_recurision_1(p,n):     # 1式
    if n==0:
        return 0
    else:
        res = p[n]
        for i in range(1,n):
            res = max(res,cut_rod_recurision_1(p,i) + cut_rod_recurision_1(p,n-i))
        return res

print(cut_rod_recurision_1(p,9))

def cut_rod_recurision_2(p,n):      # 2式自顶向下
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1,n+1):
            res = max(res,p[i]+cut_rod_recurision_2(p,n-i))
        return res
print(cut_rod_recurision_2(p,9))

上面两种方法是自顶向下递归实现，时间复杂度为：（2ⁿ）。

下面我们使用动态规划解法。
动态规划思想：每个子问题只求解一次，保存求解结果；之后需要此问题时，只需查找保存结果。

自底向上的求法：

def cut_rod_dp(p,n):
    r = [0]
    for i in range(1,n+1):         # 这一步是表示长度i的情况
        res = 0
        for j in range(1,i+1):        # 这一步是指在第j种分法的最大值
            res = max(res,p[j]+r[i-j])
        r.append(res)
    return r[n]
print(cut_rod_dp(p,10))

上面的时间复杂度为：O（n²）

最后需要进行重构解，我们不仅要知道输出最优解，还要知道输出最优分割方案。
我们在上面的方法再加上一个列表来存放每个子问题（长度为i的钢条的第一次左边切割的长度）的方案，制作成下面列表。

i	0	1	2	3	4	5	6	7	8	9	10
r[i]	0	1	5	8	10	13	17	18	22	25	30
s[i]	0	1	2	3	2	2	6	1	2	3	10

r里面存放的是最高价格，s里面存放的是左边第一刀切的位置。

def cut_rod_extend(p,n):
    r = [0]
    s = [0]
    for i in range(1,n+1):
        res_r = 0   # 价格最大值
        res_s = 0   # 价格最大值对应的方案的左边不切割部分的长度
        for j in range(1,i+1):
            if p[j]+r[i-j] > res_r:
                res_r = p[j] + r[i-j]
                res_s = j
        r.append(res_r)
        s.append(res_s)
    return r[n],s

# 显示得到在哪个位置切
def cut_rod_solution(p,n):
    r,s = cut_rod_extend(p,n)
    temp = []
    while n>0:
        temp.append(s[n])
        n-=s[n]
    return temp

r,s = cut_rod_extend(p,10)
print(s)
print(cut_rod_solution(p,9))

通过上面的各种方法，我们可以发现动态规划问题的关键特征：
1、最优子结构
原问题的最优解中涉及多少个子问题，
在确定最优解使用哪些子问题时，需要考虑多少种选择
2、重复子问题

二、最长公共子序列（LCS）：给定两个序列X和Y，求X和Y长度最长的公共子序列。
例如：X=“ABBCBDE”，Y=“DBBCDB”，LCS(X,Y)=“BBCD”

一个序列的子序列是在该序列中删去若干元素后得到的序列，例如："ABCD"和"BDF"都是"ABCDEFG"的子序列，子序列不需要在原序列中是连续的。

应用场景为：字符串相似度比对

思路：
1、求出最优解递推式：（c[i,j]表示X_i和Y_j的LCS长度）

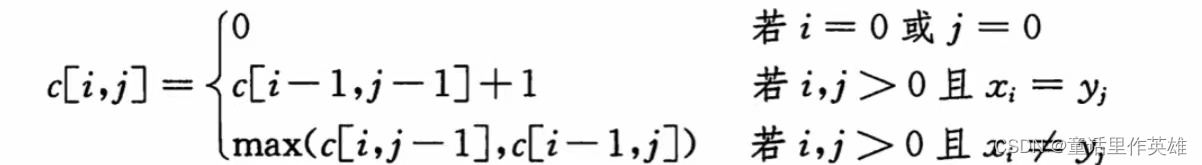
我们可以理解：就是在x轴的值和y轴的值相同的那个坐标位置上，当前点的最长公共子序列的长度就是（x-1，y-1）位置的最长公共子序列的长度+1，其他非相同位置就在（x，y-1）和（x-1，y）中取一个最长公共子序列（即max（（x，y-1），（x-1，y）））。例如：求a="ABCCDAB"与b=“BDCABA"的LCS：由于最后一位"B”!=“A”，所以LCS（a,b）应该来源于LCS（a[:-1],b）与LCS（a,b[:-1]）中更大的那一个。

我们看下图理解：

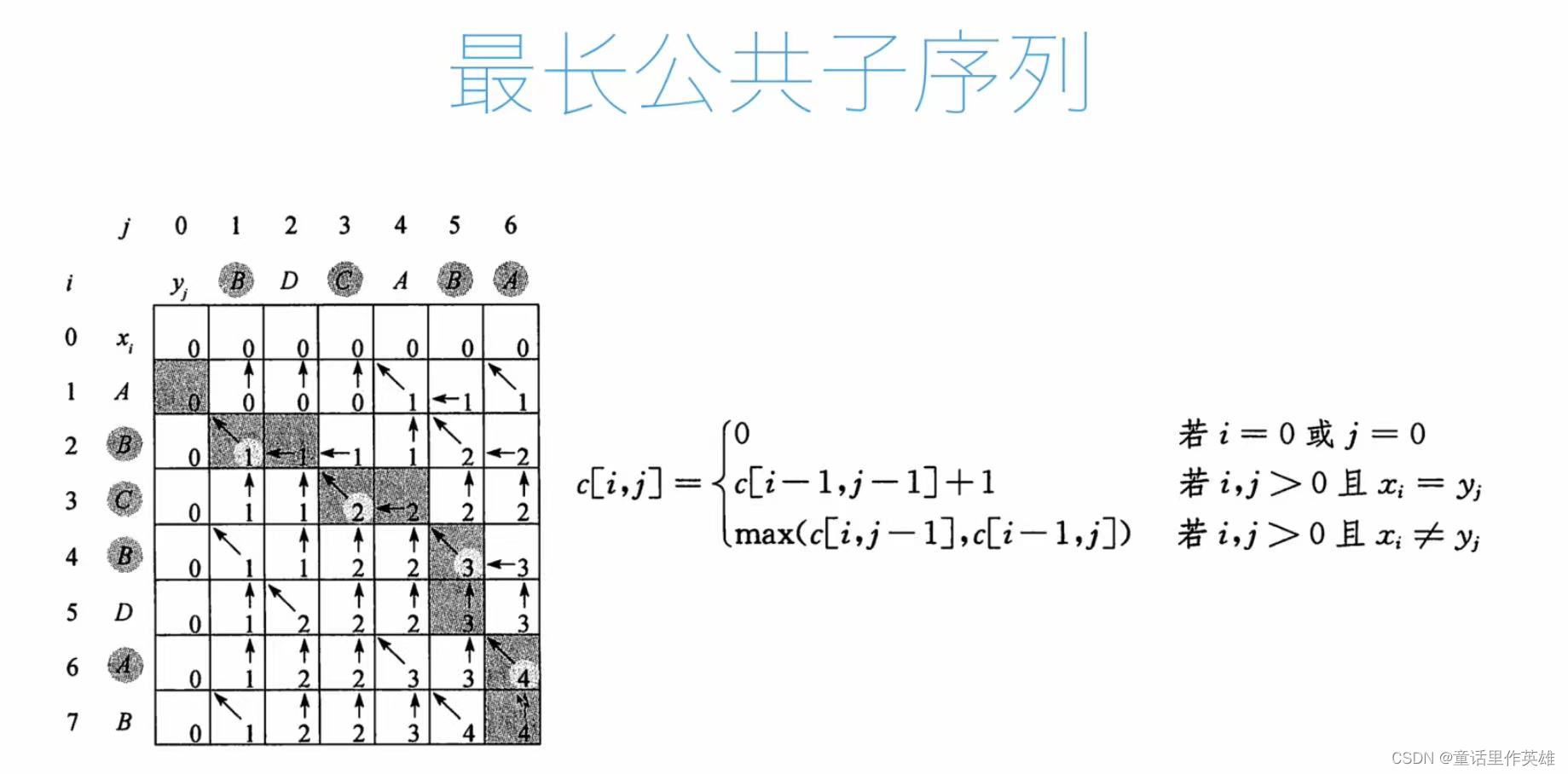
代码如下：

def lcs_length(x,y):    # x表示行，y表示列
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n+1)] for _ in range(m+1)]
    for i in range(1,m+1):
        for j in range(1,n+1):
            if x[i-1] == y[j-1]:     # 因为我们的i和j是从1开始的，但是我们在字符串和列表中查找的话是从0开始的，所以需要-1
                c[i][j] = c[i-1][j-1] + 1
            else:
                c[i][j] = max(c[i-1][j],c[i][j-1])
    for _ in c:
        print(_)
    return c[m][n]

print(lcs_length("ABCBDAB","BDCABA"))

# 输出
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 1, 1]
[0, 1, 1, 1, 1, 2, 2]
[0, 1, 1, 2, 2, 2, 2]
[0, 1, 1, 2, 2, 3, 3]
[0, 1, 2, 2, 2, 3, 3]
[0, 1, 2, 2, 3, 3, 4]
[0, 1, 2, 2, 3, 4, 4]
4

我们知道最长公共子序列后，还要知道这几个序列是具体多少，这个时候我们看图，可以发现只要是路径上斜着增加长度的几个点，就是我们需要保留的数值，我们可以通过这个属性，来记录，最后得到完整的内容。

我们新建立一个列表b，给三种情形进行赋值在b。
代码如下：

def lcs(x,y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n+1)] for _ in range(m+1)]
    b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]   # 1是左上方，2是上方，3是左方
    for i in range(1,m+1):
        for j in range(1,n+1):
            if x[i-1] == y[j-1]:     # 因为我们的i和j是从1开始的，但是我们在字符串和列表中查找的话是从0开始的，所以需要-1
                c[i][j] = c[i-1][j-1] + 1
                b[i][j] = 1
            elif c[i-1][j] > c[i][j-1]:        # 来自上
                c[i][j] = c[i][j-1]
                b[i][j] = 2
            else:
                c[i][j] = c[i-1][j]
                b[i][j] = 3
    return c[m][n],b

# print(lcs_length("ABCBDAB","BDCABA"))
c,b = lcs("ABCBDAB","BDCABA")
for _ in b:
    print(_)

# 输出
[0, 0, 0, 0, 0, 0, 0]
[0, 3, 3, 3, 1, 3, 1]
[0, 1, 3, 3, 2, 1, 3]
[0, 2, 3, 1, 3, 2, 2]
[0, 1, 3, 2, 3, 1, 3]
[0, 2, 1, 3, 3, 2, 3]
[0, 3, 2, 3, 1, 3, 1]
[0, 1, 3, 3, 2, 1, 3]

我们再建立一个函数调用上面的方法并且输出我们得到的最长公共子序列，
代码如下：

def lcs_trackback(x,y):
    c,b = lcs(x,y)
    i = len(x)
    j = len(y)
    res = []
    while i>0 and j>0:
        if b[i][j] ==1:     # 来自左上方=>匹配
            res.append(x[i-1])
            i -= 1
            j -= 1
        elif b[i][j] == 2:     # 来自上方
            i -= 1
        else:                # 来自左方
            j -= 1
    return "".join(reversed(res))


print(lcs_trackback("ABCBDAB","BDCABA"))

# 输出
BDAB