降维的基本知识点总结
降维方法分为线性和非线性降维,非线性降维又分为基于核函数和基于特征值的方法。
- 线性降维: PCA、ICA、LDA、LFA、LPP
- 非线性降维:
- 基于核函数的方法:KPCA、KICA、KDA
- 基于特征值的方法: ISOMAP、LLE、LE、LPP、LTSA、MVU
或者降降维方法如下图分类:

降维的作用
- 降低时间复杂度和空间复杂度。
- 节省了提取不必要的特征开销
- 去掉数据集中夹杂的噪音。
- 较简单的模型在较小的数据集上具有更高的鲁棒性。
- 当数据能有较少的特征进行解释,我们可以更好的解释数据,使得我们可以提取知识。。
- 实现数据的可视化。
降维的目的
用来进行特征选择和特征提取。
- 特征选择:选择重要的特征子集,删除其余特征
- 特征提取:由原始特征形成较少的新特征。
在特征提取中,我们要找到 k k k个新的维度的集合,这些维度是原来k个维度的集合,这个方法可以是监督的,也可以是非监督的,如PCA是非监督的,LDA是监督的。
子集选择
对于
n
n
n个属性,有2n个可能的子集。穷举搜索找出属性的最佳子集可能是不现实的。特别是当n的数据类目增加时,通常使用压缩搜索空间的启发式算法,通常这些方法时典型的贪心算法,在搜索属性空间时,总是做看上去是最佳选择,它们的策略是局部最优选择, 期望由此导出全局最优解,在实践中,这些贪心算法是有效的,并可以逼近最优解。
子集选择的缺点:
降维的本质
学习一个映射函数 f f f: x x x到 y y y。(x是原数据点的表达,目前最多是用向量来表示, Y Y Y是数据点映射后的低维向量表达) f f f可能是显示的、隐式的,线性的、非线性的。
主成分分析PCA
- 降原始数据的每一个样本用向量表示,把所有样本组合起来构成样本矩阵,通常对样本矩阵进行中心化处理,得到中心化样本矩阵。
- 求中心化后样本矩阵的协方差。
- 求协方差矩阵的特征值和特征向量。
- 将求出的特征值按从大到小顺序排列,并将其对应的特征向量按照此顺序组合成一个映射矩阵,根据指定的PCA保留的特征个数取出来映射矩阵前n行或前n列作为最终的映射矩阵。
- 用映射矩阵对数据进行映射,达到数据降维的目的。
PCA示例的小插曲:TF-IDF
TF-IDF: 是一种用于信息检索和文本挖掘的常用加权技术,是一种统计方法,用于评估一个词对于一个文本集和一个语料库中其中一份文件的重要程度,包括两部分:词频和逆文档频率。
- 协方差矩阵对角上是方差,非对角线上是协方差,协方差是衡量两个变量同时变化的变化程度。
- PCA推导——最大方差理论
- 在信号处理中,认为信号具有较大的方差,噪音具有较小的方差,信噪比越大越好,PCA遵循投影后的样本点间方差最大原则。
LDA
- 线性判别式分析,是模式识别中的经典算法。
- 是一种监督学习的降维技术,它的数据集中每个样本都是有类别输出的。
- 思想:投影后类内距离最小,类间距离最大。
- 线性判别: 将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果。投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离。这是一种有效的特征提取方法。使用这个方法,能使得投影后模式样本的类间散布矩阵最大,且同时类内散布矩阵最小。
与PCA相比较
- 共同点,都属于线性方法。
- 在降维时都采用矩阵分解的方法
- 都假设数据符合高斯分布。
- 不同点:
- LDA是有监督的。
- 不能保证投影到的坐标系是正交的,(根据类别的标注,关注分类能力)
- 降维直接与类别的个数有关,与数据本身维度无关,
- 原始数据是n维的,有c个类别,降维后一般是到c-1维
- 可以用于降维,还可以用于分类。
- 选择分类性能最好的投影方向。
LLE
属于流行学习的一种,和传统的PCA和LDA相比,不在是关注样本方差的降维方法,而是一种关注降维时保持样本局部的线性特征。
LLE将高维流形分成许多小块,每一小块可以用平面代替,然后再在低维中重新拼合起来,且要求保留各点之间的拓扑关系不变。
LLE思想
首先假设数据在较小的局部时线性的,即某一个数据能够用它邻域中的几个样本来线性表示,可以通过 k − k- k−近邻的思想来找到它的近邻点。在降维之后,希望样本点对应的投影尽量保持同样的线性关系,。即投影前后线性关系的权重参数不变或者改变很小。
LLE算法推导
- 首先确定邻域大小的选择
- 需要找到某个样本 x i x_i xi和 k k k个最近邻之间的线性关系。
- 由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值
ISOMAP(等距特征映射)
以线性流形学习方法MDS为理论基础,将经典MDS方法中的欧式距离替换为
tSNE
TSNE是由SNE衍生出的一张算法,SNE最早出现在2002年**,改变了MDN和ISOMAP中基于距离不变的思想**,将高维映射到低维的同时,尽量保证相互之间的分布概率不变,SNE将高维和低维中的样本分布都看作高斯分布,而TSNE将低维中的坐标当作T分布,这样的好处是为了让距离大的簇之间距离拉大,从而解决了拥挤问题。从SNE到TSNE之间,还有一个对称SNE,其对SNE有部分改进作用。
SNE算法




对称SNE
就是让高维和低维中的概率分布矩阵是对称的,能方便计算,但是对拥挤问题无法改进。
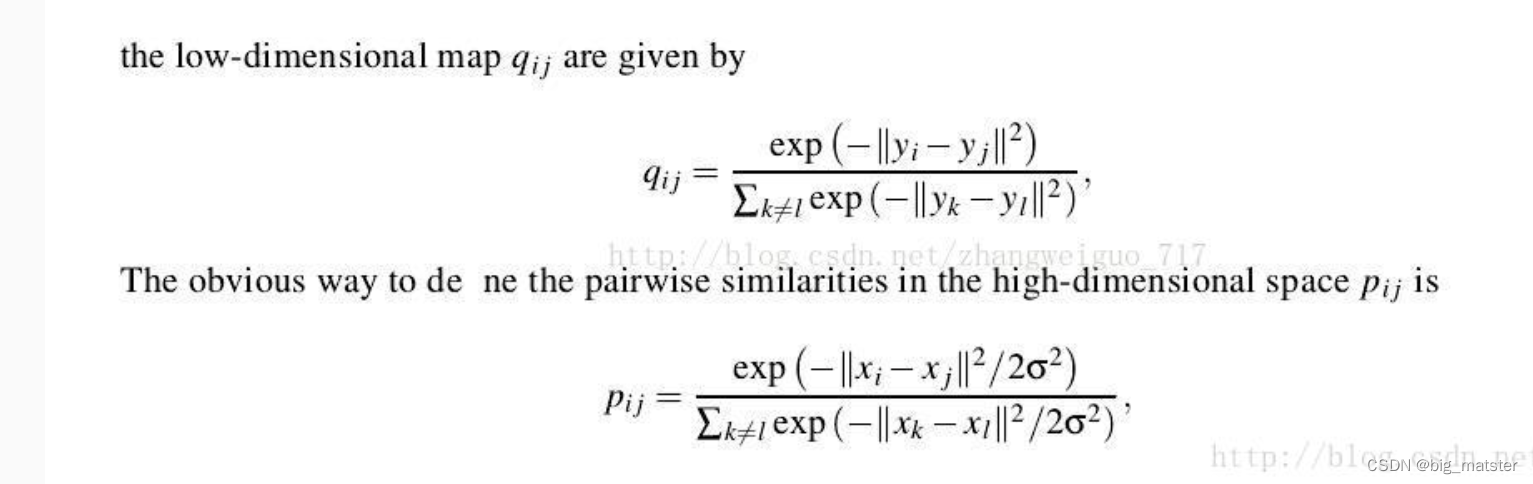

TSNE

经验
- 总结了以下降维方法总称,后两个算法用到时候自己在开始查找,将其全部搞定都行啦的样子与打算。








 文章介绍了降维的基本概念,包括线性降维(如PCA、LDA)和非线性降维(如KPCA、LLE),以及它们的目的和作用,如减少复杂度、去除噪声和数据可视化。降维方法还包括基于特征值的算法如ISOMAP,以及解决拥挤问题的TSNE。此外,讨论了特征选择的子集搜索策略和降维的本质,即学习映射函数以降低数据的维度。
文章介绍了降维的基本概念,包括线性降维(如PCA、LDA)和非线性降维(如KPCA、LLE),以及它们的目的和作用,如减少复杂度、去除噪声和数据可视化。降维方法还包括基于特征值的算法如ISOMAP,以及解决拥挤问题的TSNE。此外,讨论了特征选择的子集搜索策略和降维的本质,即学习映射函数以降低数据的维度。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










