23蓝桥杯算法c组python题解(二)

第三题  三国游戏：详细题目如下

问题分析：

        根据题意可知，我们需要找出每个国家获胜分别最多发生的事件数量，最后再选择三者中事件最多的即可。可以利用贪心思想，通过寻找局部最优，来得到总体最优。

代码如下：

import os
import sys

# 贪心算法：先找局部最优，最后得到总体最优解
n = int(input())

A = list(map(int, input().split()))
B = list(map(int, input().split()))
C = list(map(int, input().split()))

# 定义一个函数来寻找其中一个赢得胜利的事件发生的最大次数
def win(A, B, C): # 假设A获胜（A可以是魏蜀吴三家）
  Win_times = []
  ans = 0

  for i in range(n):
    w = (A[i] - B[i] - C[i]) #记录各次时间中A增加的兵力是否大于二者之和
    Win_times.append(w)
  Win_times = sorted(Win_times, reverse=True) # 将记录的事件结果从大到小排序
  counter = 0
  
  for w in Win_times: #从大到小检测记录的事件结果，大于零则事件计数器加一，小于0则退出循坏
    ans += w
    counter += 1
    if ans <= 0:
      break
  
  if counter < 2: # counter小于2则说明，记录的第一个事件就小于0，即最大的小于0，则该国无法获胜
    return -1
  else:
    return (counter-1)
  
Times_things = max(win(A, B, C), win(B, A, C), win(C,B,A))
print(Times_things)

第四题 平均：

       

问题分析：

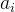
        本题可以利用空间换时间的思想。首先，构建哈希表来重新存储数组数据。哈希表的结构如下：{key =   [0,9] : value = [] }，依次将数组中的数据存入，哈希表的键为数，相对于的值为修改所需要的代价所组成的列表。之后，遍历哈希表，查看每个键所对应的列表长度，当列表长度大于题目所要求的平均长度时，则选择列表中前x代价加入总代价（x为列表长度减去平均长度）。注意，本题只要求我们计算修改代价，无需纠结如何修改，只需将多于平均长度的数的代价加入计算即可。

代码如下：

import os
import sys
import collections

n = int(input())
nums_dj = []
for _ in range(n):
  nums_dj.append([int(i) for i in input().split()])

average_time = n // 10
cost = 0

# 建立哈希表进行存储
mp = collections.defaultdict(list)
for i in range(n):
  key = nums_dj[i][0]
  value = nums_dj[i][1]
  mp[key].append(value)

for key, values in mp.items():
  if len(values) > average_time:
    for j in range(len(values) - average_time):
      values_sorted = sorted(values)
      cost += values_sorted[j]

print(cost)

第五题 填充 

        

        

问题分析：

        本题因为一次需要判断两个字符，可以采用双指针的方法。具体逻辑为，定义一个 left = 0指针和 right = left + 1指针从字符最左侧开始遍历。判断left是否等于right，或者是否其中至少有一个指针为'?'字符：若判断成功，则计数器加一，left直接加2，right = left + 1；否则， left = left + 1， rght = left + 1。

代码如下：

import os
import sys

strings = input()

# 双指针
counter = 0
left = 0
right = left + 1
while left < len(strings) - 1:
  if strings[left] == strings[right] or strings[left] == '?' or strings[right] == '?':
    counter += 1
    left += 2
    right = left + 1
  else:
    left += 1
    right = left + 1

print(counter)