数学之美笔录(1):统计语言模型

统计语言模型 (Statistical Language Models)

介绍
　　在语言处理领域，比如翻译、识别语音、文字识别和进行海量文献的自动检索，出现了两种最基本的方法。第一种方法比较直接，就是让机器像人一样理解语言。为了解决这个问题，人们想到的办法就是让机器模拟人类进行学习 - 学习人类的语法、分析语句等等。遗憾的是，几十年过去了，在计算机处理语言领域，基于这个语法规则的方法几乎毫无突破。

　　第二种方法就是利用统计数学方法，首先成功利用数学方法解决自然语言处理问题的是语音和语言处理大师贾里尼克 (Fred Jelinek)。当时贾里尼克在 IBM 公司做学术休假 (Sabbatical Leave)，领导了一批杰出的科学家利用大型计算机来处理人类语言问题。统计语言模型就是在那个时候提出的。

统计模型和马尔科夫假设
　　举个简单例子：如何判断一个文字序列是否能构成一个大家能理解的句子。对这个问题，我们可以建立一个简单的统计模型。
　　如果 S 表示一连串特定顺序排列的词 w1， w2，…， wn ，换句话说，S 可以表示某一个由一连串特定顺序排练的词而组成的一个有意义的句子。我们用 P(S) 来表示其出现概率。利用条件概率的公式，S 这个序列出现的概率等于每一个词出现的概率相乘，于是P(S) 可展开为：
P(S) = P(w1)P(w2|w1)P(w3| w1 w2)…P(wn|w1 w2…wn-1)
　　其中 P (w1) 表示第一个词w1 出现的概率；P (w2|w1) 是在已知第一个词的前提下，第二个词出现的概率；以次类推。不难看出，到了词wn，它的出现概率取决于它前面所有词。从计算上来看，各种可能性太多，无法实现。因此我们假定任意一个词wi的出现概率只同它前面的词 wi-1 有关(即马尔可夫假设），于是问题就变得很简单了。现在，S 出现的概率就变为：
P(S) = P(w1)P(w2|w1)P(w3|w2)…P(wi|wi-1)…
　　这里是最简单的二元模型，也可以假设一个词又前面N-1个词决定，也就是N-1阶马尔科夫假设（N元模型），模型复杂些。

　　那么如何估计 P (wi|wi-1)呢？对语料库进行统计，只要数一数这对词（wi-1,wi) 在统计的文本中出现了多少次，以及 wi-1 本身在同样的文本中前后相邻出现了多少次，然后用两个数一除就可以了，P(wi|wi-1) = P(wi-1,wi)/ P (wi-1)。
　　当然，真正实现一个好的统计语言模型还有许多细节问题需要解决。贾里尼克和他的同事的贡献在于提出了统计语言模型，而且很漂亮地解决了所有的细节问题。

　　在 Google 的中英文自动翻译中，用的最重要的就是这个统计语言模型。去年美国标准局(NIST) 对所有的机器翻译系统进行了评测，Google 的系统是不仅是全世界最好的，而且高出所有基于规则的系统很多。
这也说明了统计数学模型方法的有效性。

　　前面提到的是最简单的二元模型，也可以假设一个词又前面N-1个词决定，也就是N-1阶马尔科夫假设（N元模型），模型复杂些。实际应用中用的最多的是N=3的三元模型。在二元模型中，我们每次只需要考虑两个变量，而在三元模型中，我们每次只需要考虑3个变量，变量越少，计算越是简便，当然这也说明模型简单，不能很好地模拟实际情况。其实这也是一个需要平衡的过程，n越大越能反映出真实的分布情况，但是相应地也带来很大的计算代价；n越小，虽然计算方便，但是模型就越简单，不能很好的反映出实际的概率分布。
　　为什么实际应用中N都是取较小的值呢？一是因为N元模型的空间复杂度是指数级的，所以不能取得太大，而是因为当N>4时，其效果提升已经不明显了，反而会占据大量资源。谷歌的罗塞塔翻译系统使用的是五元模型。

模型的训练、零概率问题和平滑方法
　　前面提到的模型训练方法，似乎非常简单。比如对于二元模型，就是拿两个数字， 在语料中同现的次数和在语料中单独出现的次数，计算一下比值即可。但问题是，如果同现的次数怎么办，是否意味着条件概率| ？反过来如果和都只出现了一次，是否敢得出|这样非常绝对的结论？这就涉及到统计的可靠性问题了。

　　那么如何正确地训练一个语言模型呢？一般而言，对于统计，统计量越大，统计结果越接近真实情况。
　　一个直接的办法就是增加数据量，但是即使如此，依然会遇到零概率或者统计量不足的问题。假定要训练一个汉语的语言模型，汉语的词汇量大致是20 万这个量级，训练一个三元模型就有200 000^3 = 8 × 1015 个不同的参数。假如从互联网上刨去垃圾数据，有100 亿个有意义的中文网页，这已经是相当高估的数据，每个网页平均1 000 词。那么，即使将互联网上全部的中文内容都用作训练，依然只有10^13，因此，如果用直接的比值计算概率，大部分条件概率依然是零，这种模型我们称之为“不平滑”。在实际应用中，统计语言模型的零概率问题是无法回避的，必须解决。

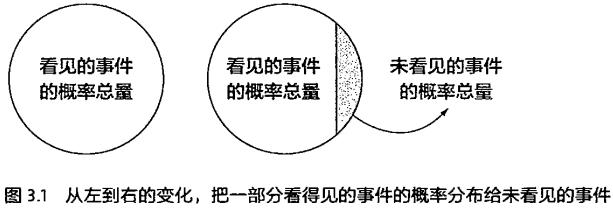
　　训练统计语言模型的艺术就在于解决好统计样本不足时的概率估计问题。1953 年古德（I. J. Good）在他老板图灵（Alan Turing）（就是计算机科学史上的图灵）的指导下，提出了在统计中相信可靠的统计数据，而对不可信的统计数据打折扣的一种概率估计方法，同时将折扣出来的那一小部分概率给予未看见的事件（Unseen Events）。古德和图灵还给出了一个很漂亮的重新估算概率的公式，这个公式后来被称为古德-图灵估计（Good-Turing Estimate）。
　　其原理是这样的：对于没有看见的事件，我们不能认为它发生的概率就是零，因此我们从概率的总量中，分配一个很小的比例给予这些没有看见的事件。这样一来，看见的那些事件的概率总和就要小于1了，因此，需要将所有看见的事件概率调小一点。至于小多少，要根据“越是不可信的统计折扣越多”的方法进行。

语料的选取问题
　　模型训练中另一个重要的问题就是训练数据，或者说语料库的选取。如果训练语料和模型应用的领域相脱节，那么模型的效果通常要大打折扣。比如对于建立一个语言模型，如果应用是网页搜索，它的训练数据就应该是杂乱的网页数据和用户输入的搜索串，而不是传统的、规范的新闻稿，即使前者夹杂着噪音和错误。
　　这里有一个很好的例子，来自于腾讯搜索部门。最早的语言模型是使用《人民日报》的语料训练的，因为开发者认为这些语料干净、无噪音。但是实际的效果就比较差，经常出现搜索串和网页不匹配的例子。后来改用网页的数据，尽管它们有很多的噪音，但是因为训练数据和应用一致，搜索质量反而好。

　　训练数据通常是越多越好。虽然通过上节介绍的平滑过渡的方法可以解决零概率和很小概率的问题，但是毕竟在数据量多的时候概率模型的参数可以估计得比较准确。高阶的模型因为参数多，需要的训练数据也相应会多很多。遗憾的是，并非所有的应用都能得到足够的训练数据，比如说机器翻译的双语语料就非常少，在这种情况下片面追求高阶的大模型就变得一点意义也没有了。

　　在训练数据和应用数据一致并且训练量足够大的情况下，训练语料的噪音高低也会对模型的效果产生一定的影响，因此，在训练以前有时需要对训练数据进行预处理。一般情况下，少量的（没有模式的）随机噪音清除起来成本非常高，通常就不做处理了。但是对于能找到模式（Pattern）的、量比较大的噪音还是需要进行过滤的，而且它们也比较容易处理，比如网页文本中大量的制表符。因此，在成本不高的情况下，过滤训练数据还是需要做的。