奇异值分解（SVD）

前提：适用于任何矩阵，没有限制。对于任何矩阵A，都是对称矩阵，且的特征值都大于或者等于0。

奇异值分解(Singular Value Decomposition)是一种重要的矩阵分解方法，可以看作是对称方阵在任意矩阵上的推广。

矩阵的奇异值分解在矩阵特征值问题、最小二乘法问题及广义逆矩阵问题等方面有重要应用。它体现了线性变换的旋转、缩放和投影的功效。

假设A为一个m*n阶实矩阵，则存在一个分解使得：

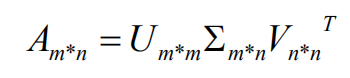
通常将奇异值由大到小排列，这样 Σ 便能由 A 唯一确定了。

不特征值、特征向量的概念相对应，则：

• Σ 对角线上的元素称为矩阵 A 的奇异值;
• U 和 V 称为 A 的左/右奇异向量矩阵。