浅析互信息（信息增益）

互信息(Mutual Information)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。这是百度百科的定义，本文的重点是从不同的角度去理解互信息，介绍一些基本的规律，为了简单本文只对其离散的情况考虑。
在介绍互信息前首先更应该知道什么是信息熵，信息熵是香农从物理理论中的热熵引入到信息论中的，热熵是一种描述分子状态混乱程度的物理量，信息论中的熵是对信源不确定性的描述，是对体系信息量的表示。熵的定义：
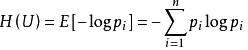![熵定义](https://img-blog.csdn.net/20150330204643565)其中Pi表示信源中信号i出现的概率。
互信息的角度，一个随机变量的引入，对于另一个随机变量混乱度降低量的。一个事件的引入，消除另一个事件的不确定性。
信息增益的角度，与互信息相似，计算某个特征是否命中前，样本的分布拥有一个信息熵，计算后计算命中特征样本与未命中样本特征的信息增益，然后计算出计算后熵的期望，计算前后的熵差就是信息增益。
另外互信息是具有非负性的，证明：![这里写图片描述](https://img-blog.csdn.net/20150330210536018)