几种常见的计算机视觉中的损失函数原理理解&分析
摘要 机器学习任务中适用损失函数来计算描述预测结果和实际事实之间的差距,通过损失函数来量化这个差距从而判断预测的错误程度。因此选择适当的损失函数将有助于获得较好的结果。这里将尝试分析理解计算机视觉中一些基本的损失函数和图像分类、图像检测以及图像分割任务中常用的主流损失函数。
基本的损失函数
L2 Loss
这是计算损失函数最基本的损失函数,PyTorch中也将其命名为torch.nn.MSELoss。这依赖于两个向量[预测和真实标签]之间的Euclidean距离(欧氏距离)。它有几个别称分别为
- L2 范数损失
- 最小均方值偏差(LSD)
- 最小均方值误差(LSE)
它是把目标值与模型输出(估计值)做差然后平方得到的误差,L2 Loss 对异常值非常敏感,因为误差是平方的。例如:真实值为1,预测10次,有一次预测值为1000,其余次的预测值为1左右,显然loss值主要由1000主宰。

Pytorch使用范例:
import torch
import numpy as np
a = torch.tensor([[1, 2], [3, 4]], dtype=torch.float)
b = torch.tensor([[3, 5], [8, 6]], dtype=torch.float)
loss_fn1 = torch.nn.MSELoss()
loss1 = loss_fn1(a.float(), b.float())
print(loss1) # 10.5000
使用场景
回归任务、数值特征不大、问题维度不高
Softmax 函数
分类的损失函数一般都要求算法的每个标量输出输入概率 p在0至1之间且和为1。但是预测值并非总是如此,我们可以使用Softmax 函数(非线性函数)将预测值变为概率在0至1之间且和为1。因此Softmax 函数也称为归一化指数函数,其公式如下:
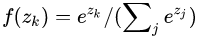
softmax常用来进行多分类,假如有一个4x1向量z^{[L]}=[5,2,-1,3],softmax的计算过程如下所示


Pytorch使用范例:
import torch
import torch.nn.functional as F
x= torch.Tensor( [ [1,2,3,4],[1,2,3,4],[1,2,3,4]])
y1= F.softmax(x, dim = 0) #对每一列进行softmax
y2 = F.softmax(x,dim =1) #对每一行进行softmax
SmoothL1 Loss
简单来说就是平滑版的L1 Loss。
原理
SoothL1Loss的函数如下:

仔细观察可以看到,当预测值和ground truth差别较小的时候(绝对值差小于1),其实使用的是L2 Loss;而当差别大的时候,是L1 Loss的平移。SooothL1Loss其实是L2Loss和L1Loss的结合,它同时拥有L2 Loss和L1 Loss的部分优点。
- 当预测值和ground truth差别较小的时候(绝对值差小于1),梯度不至于太大。(损失函数相较L1 Loss比较圆滑)
- 当差别大的时候,梯度值足够小(较稳定,不容易梯度爆炸)。

使用场景:
回归、当特征中有较大的数值、适合大多数问题
图像分类中的损失函数
在图像分类中,经常使用softmax+交叉熵作为损失函数
CROSS-ENTROPY LOSS
交叉熵主要刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,H(p,q)为交叉熵,则

那么该公式如何表示,举个例子,假设N=3,期望输出为 p=(1,0,0) 实际输出 q1=(0.5,0.2,0.3),q2=(0.8,0.1,0.1) ,那么:
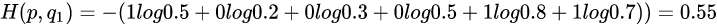
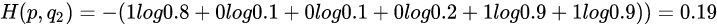
通过上面可以看出,q2与p更为接近,它的交叉熵也更小。
CrossEntropyLoss()损失函数结合了nn.LogSoftmax()和nn.NLLLoss()两个函数。它在做分类(具体几类)训练的时候是非常有用的,如上所述,softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类。
- Cross Entropy Loss Function交叉熵损失函数是使用对数(loge)的更高级的损失函数。与L2 Loss 相比,这有助于加快对神经网络的训练。
- 在二分类的情况下交叉熵损失函数被称为BCE Loss,模型最后需要预测的结果只有两种情况,对于每个类别我们的预测得到的概率为 p 和 1-p 。此时表达式为:

其中:

- 交叉熵(多类别误差)是对二分类的扩展的公式如下。也称为分类交叉熵。

其中:

Pytorch二分类交叉熵损失BCE Loss:
import torch
loss = torch.nn.BCEWithLogitsLoss()
#preds预测值 如:[-0.4004, 0.2050, 0.7746]
preds= torch.randn(3, requires_grad=True)
#target输入是onthot向量,target是真实标签,,可以是[0,0,1,1,0...]多个值为1
target = torch.empty(3).random_(2)#[0,1,1]
output = loss(pred, target)# [0.4959]
Pytorch 多分类交叉熵 CrossEntropy Loss:
#五分类范例
loss = torch.nn.CrossEntropyLoss()
preds= torch.randn(3, 5, requires_grad=True)
#target输入不是onthot向量,target是真实标签,是稀疏的标签值;tensor([4, 2, 4])
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(predsinputs, target)
计算原理
- 1、Softmax后的数值都在0~1之间,所以ln之后值域是负无穷到0;
- 2、然后将Softmax之后的结果取log,将乘法改成加法减少计算量,同时保障函数的单调性;
- 3、NLLLoss的结果就是把上面的输出与Label对应的那个值拿出来(下面例子中就是:将log_output\logsoftmax_output中与y_target对应的值拿出来),去掉负号,再求均值。
import torch
import torch.nn as nn
x_input=torch.randn(3,3)#三分类随机生成输入
print('x_input:\n',x_input)
y_target=torch.tensor([1,2,0])#设置输出具体值 print('y_target\n',y_target)
#计算输入softmax,此时可以看到每一行加到一起结果都是1
softmax_func=nn.Softmax(dim=1)
soft_output=softmax_func(x_input)
print('soft_output:\n',soft_output)
#在softmax的基础上取log
log_output=torch.log(soft_output)
print('log_output:\n',log_output)
#对比softmax与log的结合与nn.LogSoftmaxloss(负对数似然损失)的输出结果,发现两者是一致的。
logsoftmax_func=nn.LogSoftmax(dim=1)
logsoftmax_output=logsoftmax_func(x_input)
print('logsoftmax_output:\n',logsoftmax_output)
#pytorch中关于NLLLoss的默认参数配置为:reducetion=True、size_average=True
nllloss_func=nn.NLLLoss()
nlloss_output=nllloss_func(logsoftmax_output,y_target)
print('nlloss_output:\n',nlloss_output)
#直接使用pytorch中的loss_func=nn.CrossEntropyLoss()看与经过NLLLoss的计算是不是一样
crossentropyloss=nn.CrossEntropyLoss()
crossentropyloss_output=crossentropyloss(x_input,y_target)
print('crossentropyloss_output:\n',crossentropyloss_output)
计算输出结果如下:
x_input:
tensor([[ 2.8883, 0.1760, 1.0774],
[ 1.1216, -0.0562, 0.0660],
[-1.3939, -0.0967, 0.5853]])
y_target
tensor([1, 2, 0])
soft_output:
tensor([[0.8131, 0.0540, 0.1329],
[0.6039, 0.1860, 0.2102],
[0.0841, 0.3076, 0.6083]])
log_output:
tensor([[-0.2069, -2.9192, -2.0178],
[-0.5044, -1.6822, -1.5599],
[-2.4762, -1.1790, -0.4970]])
logsoftmax_output:
tensor([[-0.2069, -2.9192, -2.0178],
[-0.5044, -1.6822, -1.5599],
[-2.4762, -1.1790, -0.4970]])
nlloss_output:
tensor(2.3185)
crossentropyloss_output:
tensor(2.3185)
直接使用pytorch中的loss_func=nn.CrossEntropyLoss()计算得到的结果与softmax-log-NLLLoss计算得到的结果是一致的。
Label Smoothing
谷歌在交叉熵的基础上,提出了label smoothing(标签平滑)防止模型在训练时过于自信地预测标签,改善泛化能力差的问题。在深度学习样本训练的过程中采用one-hot标签去进行计算交叉熵损失时,只考虑到训练样本中正确的标签位置(one-hot标签为1的位置)的损失,而忽略了错误标签位置(one-hot标签为0的位置)的损失。这样一来,模型可以在训练集上拟合的很好,但由于其他错误标签位置的损失没有计算,导致预测的时候,预测错误的概率增大。为了解决这一问题,标签平滑的正则化方法便应运而生。
对于分类问题,我们通常认为训练数据中标签向量的目标类别概率应为1,非目标类别概率应为0。传统的one-hot编码的标签向量yi为,
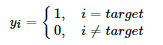
而label smoothing计算公式为

在训练网络时,交叉熵损失可由以下公式计算得到。

其中pi由对模型倒数第二层输出的logits向量z应用Softmax函数计算得到,
为了比较使用label smoothing和未使用的两种情况,举例分析如下:
使用举例:
- 例1
有一批类别总数为3的样本,从中取出一个样本,得到该样本的 one-hot 化后的标签为 [ 0 , 1 , 0 ] ,假设我们已经得到了该样本进行softmax的概率矩阵 p=[p1,p2,p3]=[0.2, 0.5,0.3],通过交叉熵损失函数计算得到loss为
loss = -(log0.5)=0.693
可以发现没有标签平滑计算的损失只考虑正确标签位置的损失,而不考虑其他标签位置的损失,这就会出现一个问题,即不考虑其他错误标签位置的损失,这会使得模型过于关注增大预测正确标签的概率,而不关注减少预测错误标签的概率,最后导致的结果是模型在自己的训练集上拟合效果非常良好,而在其他的测试集结果表现不好,即过拟合,也就是说模型泛化能力差。 - 例2
对以上的概率矩阵进行标签平滑,设平滑因子ϵ=0.1
y = (1-ϵ)[ 0 , 1 , 0 ] +ϵ[1,1,1]=[0.1,0.9,0.1]
loss = -(0.1log0.2+0.9log0.5+0.1log0.3)=0.905
可以看出,平滑过后的样本交叉熵损失就不仅考虑到了训练样本中正确的标签位置(one-hot标签为1的位置)的损失,也稍微考虑到其他错误标签位置(one-hot标签为0的位置)的损失,导致最后的损失增大,导致模型的学习能力提高,即要下降到原来的损失,就得学习的更好,也就是迫使模型往增大正确分类概率并且同时减小错误分类概率的方向前进。
Pytorch Label Smoothing
class LabelSmoothing(nn.Module):
"""NLL loss with label smoothing.
"""
def __init__(self, smoothing=0.0):
"""Constructor for the LabelSmoothing module.
:param smoothing: label smoothing factor
"""
super(LabelSmoothing, self).__init__()
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
# 此处的self.smoothing即我们的epsilon平滑参数。
def forward(self, x, target):
# 此处x的shape应该是(batch size * class数量),所以这里在class数量那个维度做了logsoftmax。
logprobs = torch.nn.functional.log_softmax(x, dim=-1)
# 此处的target的shape是(batch size), 应该就是每个training data的数字标签。
nll_loss = -logprobs.gather(dim=-1, index=target.unsqueeze(1))
# 把输出的shape变回(batch size)
nll_loss = nll_loss.squeeze(1)
# 在第二个维度取均值的话,应该就是对每个x,所有类的logprobs取了平均值。
smooth_loss = -logprobs.mean(dim=-1)
loss = self.confidence * nll_loss + self.smoothing * smooth_loss
return loss.mean()
应用场景
只要loss损失函数中涉及到了cross entropy,都可以应用标签平滑处理。其实质就是促使神经网络中进行softmax激活函数激活之后的分类概率结果向正确分类靠近,即正确的分类概率输出大(对应的one-hot标签为1位置的softmax概率大),并且同样尽可能的远离错误分类(对应的one-hot标签为0位置的softmax概率小),即错误的分类概率输出小。
目标检测中的损失函数
目标检测的损失函数一般由classification loss(类别或分类损失)和bounding box regression loss(位置或回归损失)组成。
分类损失
- 交叉熵损失
- (见上所述)
- focal loss
Focal Loss首次在目标检测框架RetinaNet中提出,它是对典型的交叉信息熵损失函数的改进,主要用于样本分类的不平衡问题,用改变loss的方式来缓解样本的不平衡,因为改变loss只影响train部分的过程和时间,而对推断时间影响甚小,容易拓展。
focal loss就是把(交叉熵损失)CE里的p替换为pt,当预测正确的时候,pt接近1,在FL(pt)中,其系数(1 − p t )^γ 越小(只要γ > 0 ),简单的样例比重越小,难的样例比重相对变大。


- Rankings类型的损失(DR(Distributional Ranking) Loss和AP Loss)
- DR Loss
DR Loss, 分布排序损失, Qian et al., 2020, DR loss: Improving object detection by distributional ranking
DR loss的研究背景和focal loss一样,one-stage方法中样本不平衡。它进行分布的转换以及用ranking作为loss。将分类问题转换为排序问题,从而避免了正负样本不平衡的问题。同时针对排序,提出了排序的损失函数DR loss。

- AP Loss
AP Loss, Chen et al., 2019, Towards Accurate One-Stage Object Detection with AP-Loss
AP loss也是解决one-stage方法中样本不平衡问题,同时也和DR loss类似,是一种排序loss。将单级检测器中的分类任务替换为排序任务,并采用平均精度损失(AP-loss)来处理排序问题。由于AP-loss的不可微性和非凸性,使得APloss不能直接优化。因此,本文开发了一种新的优化算法,它将感知器学习中的错误驱动更新方案和深度网络中的反向传播机制无缝地结合在一起。

回归损失
- L1 Loss
平均绝对误差(Mean Absolute Error, MAE),指模型预测值和真实值之间距离的平均值。

- L2 Loss
均方误差损失(Mean Square Error, MSE),指预测值和真实值之差的平方的平均值。

- Smooth L1 Loss
(见上) - IoU Loss

- GIoU Loss
IoU反映了两个框的重叠程度,在两个框不重叠时,IoU衡等于0,此时IoU loss恒等于1。而在目标检测的边界框回归中,这显然是不合适的。因此,GIoU loss在IoU loss的基础上考虑了两个框没有重叠区域时产生的损失。具体定义如下:

其中,C表示两个框的最小包围矩形框,R(P,G)是惩罚项。从公式可以看出,当两个框没有重叠区域时,IoU为0,但R依然会产生损失。极限情况下,当两个框距离无穷远时,R→1 - DIoU Loss
IoU loss和GIoU loss都只考虑了两个框的重叠程度,但在重叠程度相同的情况下,我们其实更希望两个框能挨得足够近,即框的中心要尽量靠近。因此,DIoU在IoU loss的基础上考虑了两个框的中心点距离,具体定义如下:
 其中,ρ表示预测框和标注框中心端的距离,p和g是两个框的中心点。c表示两个框的最小包围矩形框的对角线长度。当两个框距离无限远时,中心点距离和外接矩形框对角线长度无限逼近,R→1
其中,ρ表示预测框和标注框中心端的距离,p和g是两个框的中心点。c表示两个框的最小包围矩形框的对角线长度。当两个框距离无限远时,中心点距离和外接矩形框对角线长度无限逼近,R→1
下图直观显示了不同情况下的IoU loss、GIoU loss和DIoU loss结果:

其中,绿色框表示标注框,红色框表示预测框,可以看出,最后一组的结果由于两个框中心点重合,检测效果要由于前面两组。IoU loss和GIoU loss的结果均为0.75,并不能区分三种情况,而DIoU loss则对三种情况做了很好的区分。 - CIoU Loss
DIoU loss考虑了两个框中心点的距离,而CIoU loss在DIoU loss的基础上做了更详细的度量,具体包括:重叠面积、中心点距离、长宽比
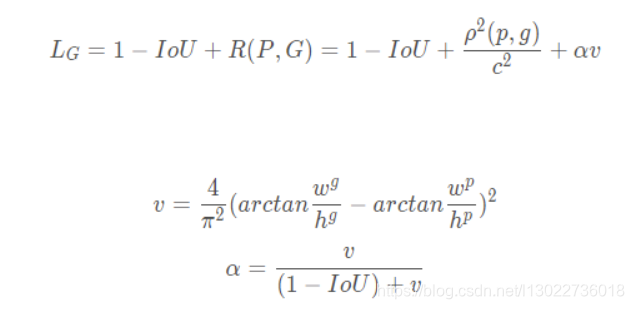

引用
https://mp.weixin.qq.com/s/k7CsGLNoNnSbnAldkafqKQ
https://blog.csdn.net/qq_44015059/article/details/109479164
https://zhuanlan.zhihu.com/p/83131026
https://blog.csdn.net/senbinyu/article/details/108310976
https://blog.csdn.net/sinat_34474705/article/details/102692382
https://blog.csdn.net/xjp_xujiping/article/details/107589950
Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression







 本文详细介绍了计算机视觉任务中常见的损失函数,包括L2Loss、Softmax、SmoothL1Loss、交叉熵损失及其变体,如FocalLoss、Ranking类型的损失等。这些损失函数在图像分类、目标检测等任务中发挥关键作用,通过量化预测与真实值的差距来优化模型。例如,Softmax用于多分类,SmoothL1Loss结合了L1和L2Loss的优点,适用于回归任务。标签平滑(LabelSmoothing)则能改善模型的泛化能力。此外,文章还探讨了目标检测中的分类损失和回归损失,如IoU系列损失函数,用于提升边界框回归的准确性。
本文详细介绍了计算机视觉任务中常见的损失函数,包括L2Loss、Softmax、SmoothL1Loss、交叉熵损失及其变体,如FocalLoss、Ranking类型的损失等。这些损失函数在图像分类、目标检测等任务中发挥关键作用,通过量化预测与真实值的差距来优化模型。例如,Softmax用于多分类,SmoothL1Loss结合了L1和L2Loss的优点,适用于回归任务。标签平滑(LabelSmoothing)则能改善模型的泛化能力。此外,文章还探讨了目标检测中的分类损失和回归损失,如IoU系列损失函数,用于提升边界框回归的准确性。
















 11万+
11万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








