快速排序的时间复杂度和空间复杂度分析（图文结合）

目录

一、平均时间复杂度以及对应的空间复杂度分析

时间复杂度：

空间复杂度：

二、最坏情况下的时间复杂度和空间复杂度

时间复杂度：

空间复杂度：

---

快速排序的代码

void QuickSort(int array[], int low, int high) {
    int i = low; 
    int j = high;
    if(i >= j) {
        return;
    }
 
    int temp = array[low];
    while(i != j) {
        while(array[j] >= temp && i < j) {
            j--;
        }
	while(array[i] <= temp && i < j) {
            i++;
        }
	if(i < j) {
            swap(array[i], array[j]);
        }
    }
 
    //将基准temp放于自己的位置，（第i个位置）
    swap(array[low], array[i]);
    QuickSort(array, low, i - 1);
    QuickSort(array, i + 1, high);

一、平均时间复杂度以及对应的空间复杂度分析

快速排序采用的是一个分治算法的思想，自定上下拆分成小的模块

时间复杂度：

（1）在对第一层里。while里的i从左向右遍历，j则相反，那么这两者共同遍历之后，一共走过的次数是n次，故第一层的时间复杂度为O（n）

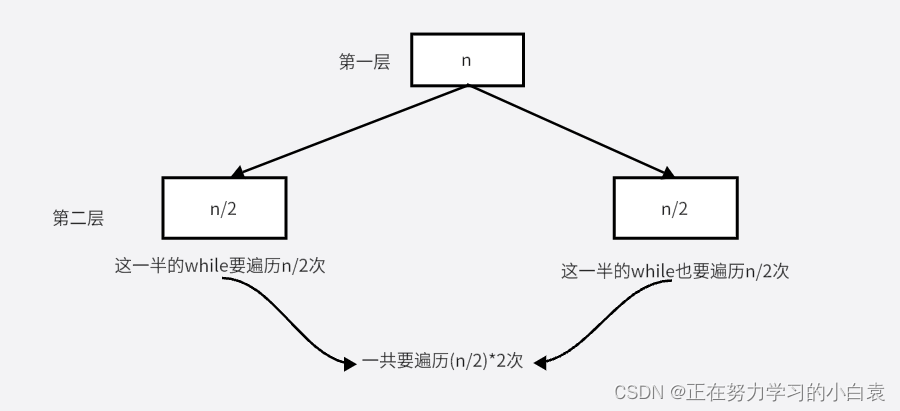
（2）在第二层中。因为有要在第一层的序列中分成两半。故下面的每层就是n/2个元素

    QuickSort(array, low, i - 1);
    QuickSort(array, i + 1, high);

在这两半中，第一半要遍历n/2遍，第二半要遍历也要遍历n/2边，所以一共要遍历(n/2)*2=n遍

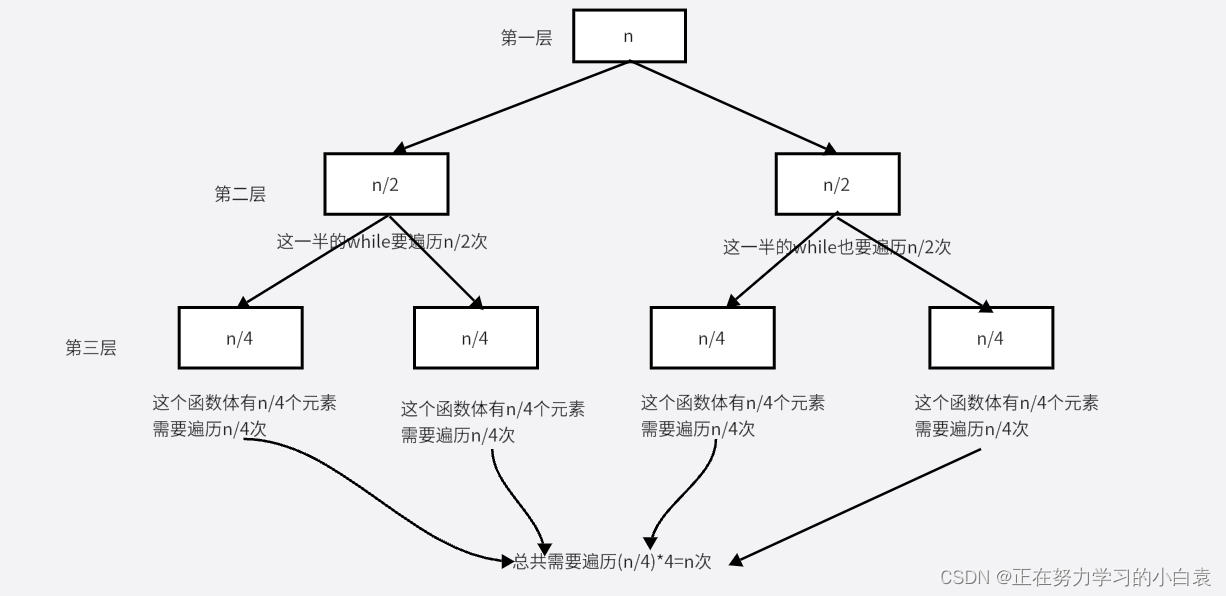
（3）在第三层中，将上一层的第一半里的n/2个元素再分为一半，同理第二半也再分为一半，所以是一共得到了4半，每一半（或者函数体）里的元素是n/4，也就是说再分出来之后的这四半里，每一半的while循环中，要遍历n/4次，因为共有4半，所以一共遍历(n/4)*4=n次

（4）对于第四层、第五层.....也是一样的道理，每一层都有n个元素需要遍历

又因为在第一层开始的后面每层，都要除以2的倍数，所以是2的x次方等于n，2^x=n，x=log2（n）,所以一共有log2(n)层

（5）因为每一层要遍历n个元素，一共有log2(n)层，因此时间总和为n*log2(n);

所以时间复杂度时O(n*log2(n))

空间复杂度：

（1）第一层,因为

QuickSort(array, low, i - 1);

QuickSort(array, i + 1, high);

这两者是先后进行的，在执行完上面代码的之后再执行下面代码，又因为从第一层开始最先执行的是QuickSort(array, low, i - 1)，且在没有回调一直递下去直到最底层时候，一共走了log2(n)次（因为有log2(n)层），每次的空间复杂度是o（1），因此最大的空间复杂度也就是log2(n)了

再执行下面的代码也是同理，最多执行了log2n次，因此综合来看，总的空间复杂度是O(log2(n))

二、最坏情况下的时间复杂度和空间复杂度

时间复杂度：

最坏的情况是当被排序的序列是基本有序序列时，所运行的时间最长，如{1,2,3,4,5,6,7}。因为如果我们取首元素为基准元素，那么开始的右指针会向左逐个扫描，找到是否有一个比首元素还要小的元素，但因为此时序列从左往右时非递减的，因此当右指针扫描到等于左指针时，才停止扫描，此时i==j==1。此时第一层需要遍历n-1次

    QuickSort(array, low, i - 1);
    QuickSort(array, i + 1, high);

（2）当进入到这两行代码时，因为i++，j--,i的值小于长度r，j的的值小于0，会被递归出来，因此只会进入到QuickSort(array, i + 1, high);代码里，进入第一层递归函数之后，l=2，r=7

所以新的一轮循环开始的时候，i=2，j=7

（3）此时又需要j从右依次扫描，需要找到比2小的元素，但因为找不到，因此又到了i==j==2的情况，因此遍历了n-2次

（4）之后整条序列中又减少了1个，进入下一个递归函数，需要遍历n-3次

（5）如此反复，每次仅仅减少一个元素

（6）当L==R时，不再遍历。总的遍历次数如下图

因此总的时间复杂度时(n-1)+(n-2)+(n-3)+……+1，总共有n-1项，等差数列求和得到(n^2-n)/2。

因此时间复杂度时O(n^2)

空间复杂度：

因为一直递归，每次递归序列元素只减少1，一共有（n-1）层，因此开辟了n-1个空间，故空间复杂度为O(n)