【AI中数学-数理统计】统计量：数据的量尺和罗盘

第五章 数理统计

第4节：统计量——数据的量尺和罗盘

在统计学中，统计量是我们用来总结、描述和推断数据的关键工具。它们就像是数据的“量尺”和“罗盘”，帮助我们理解数据的分布、趋势和变化。在AI应用中，统计量不仅是数据分析的核心，也是决策支持和模型优化的基础。不同的统计量提供了关于数据的不同视角，而它们的选择和应用直接影响着我们对数据的理解和模型的效果。

1. 统计量的定义与分类

统计量是从样本中计算得出的数值，通常用于描述数据的集中趋势、离散程度和分布特征。常见的统计量包括：

• 集中趋势统计量：例如均值、中位数、众数，描述数据的“中心”位置。
• 离散程度统计量：例如方差、标准差、极差，描述数据的“扩散”或离散程度。
• 分布形态统计量：例如偏度、峰度，描述数据分布的对称性和尾部的形态。

这些统计量帮助我们快速了解数据的基本特征，并为进一步的分析和模型构建提供基础。

2. 统计量的应用意义

在AI应用中，统计量的作用尤其重要。机器学习模型的训练过程往往依赖于数据的预处理、特征选择、异常值检测等，而这些都需要借助统计量来实现。例如，在自然语言处理（NLP）中，词频、TF-IDF等统计量被用来衡量单词的重要性；在图像分类中，像素值的均值和标准差用于图像的标准化处理。通过合理选择和使用统计量，我们能够更有效地处理和理解数据，提高模型的性能。

3. AI应用中的案例分析

接下来，我们通过三个实际的AI应用案例，深入探讨统计量在不同场景下的应用。

---

案例1：用户画像分析——电商平台的购买行为分析

在电商平台中，了解用户的购买行为是优化推荐系统、提高用户体验的关键。假设我们有一个关于用户购买记录的样本数据集，我们想通过统计量来总结用户的购买特征，包括购买金额的分布、购买频率的变化等。

步骤1：计算集中趋势统计量

• 假设我们从1000名用户中随机选取了500个用户的购买数据（每个用户的购买金额），并计算其均值和中位数：
  • 

  • 假设计算结果为：均值为50元。

  • 中位数：将所有用户的购买金额按升序排列，取中间的数值。

通过这些统计量，我们可以初步了解电商平台上用户的平均购买力及其购买行为的集中趋势。

步骤2：计算离散程度统计量

• 标准差：衡量用户购买金额的波动情况。

  

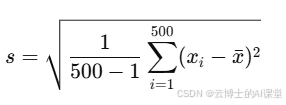
假设计算结果为10元，意味着大多数用户的购买金额在50元上下波动10元。

步骤3：分布形态的统计量

偏度（Skewness）和峰度（Kurtosis）是描述数据分布形态的两个重要统计量，它们分别反映了数据分布的对称性和尾部的特性。理解这两个概念对AI和数据分析有重要意义，尤其在建模时，偏度和峰度能帮助我们识别数据的潜在问题，从而采取合适的策略进行处理。

偏度（Skewness）

偏度用于衡量数据分布的对称性。具体而言，它反映了数据分布的“倾斜”程度：

• 正偏（右偏）：当偏度为正时，数据的右侧尾部较长，分布偏向较小的数值。此时，均值会大于中位数，说明大部分数据集中在较小的值，而少数较大的值（例如高额的购买金额）拉高了均值。
• 负偏（左偏）：当偏度为负时，数据的左侧尾部较长，分布偏向较大的数值。此时，均值会小于中位数，说明大部分数据集中在较大的值，而少数较小的值拖低了均值。
• 无偏（对称分布）：当偏度为零时，数据分布是对称的，均值和中位数基本相等。

应用场景：在电商分析中，如果购买金额的偏度为正，可能说明大部分用户的购买金额较低，少数用户的购买金额较高，拉高了平均购买额。在这种情况下，分析师可能需要进行去极值处理，以避免极端值对后续分析结果产生过大影响。

峰度（Kurtosis）

峰度用于衡量数据分布的尖锐程度，或者说是数据分布尾部的厚重程度。峰度帮助我们判断数据中是否存在异常值或极端事件：

• 高峰度：当峰度较高时，表示数据的分布比较尖锐，数据集中在均值附近，且尾部较重。这意味着数据中有较多的极端值（即异常值或离群点），可能是一些稀有事件（例如极高的购买金额）。高峰度分布通常称为**“重尾分布”**（heavy-tailed distribution）。
• 低峰度：当峰度较低时，表示数据分布较为平坦，数据大多数分布在均值周围，而尾部较轻。这种分布通常表示极端值较少，数据分布相对均匀。低峰度分布通常称为**“轻尾分布”**（light-tailed distribution）。
• 正态峰度：正态分布的峰度为 3，因此通常为了标准化，常常用超峰度来衡量，它是峰度减去 3。如果超峰度为0，则表示数据分布接近正态分布。

应用场景：在电商分析中，如果购买金额的峰度较高，说明有一些非常高额的购买金额，可能需要特别关注这些高额购买的用户群体，或者考虑对极端值进行调整。如果峰度较低，说明数据分布较为均匀，极端值较少，可能无需做去极值处理。

---

案例2：金融风险评估——股票收益波动性分析

在金融领域，评估股票的波动性是投资决策的重要依据。假设我们通过历史数据来分析一只股票的日收益率，我们希望通过标准差等统计量来衡量这只股票的波动性。

步骤1：计算收益率

• 假设我们有一个30天的股票价格数据集，通过日收盘价计算出每日的收益率。收益率可以通过如下公式计算：

  

步骤2：计算集中趋势统计量

• 均值收益率：计算30天收益率的均值，得到该股票的平均每日收益率。

  

假设计算结果为0.05，即该股票的平均日收益为5%。

步骤3：计算波动性（标准差）

• 标准差：计算收益率的标准差，衡量股票价格的波动程度。

  

假设计算结果为2%，即该股票的日收益波动为2%。

通过这些统计量，我们可以得出该股票的收益风险水平，并根据风险承受能力做出相应的投资决策。

---

案例3：深度学习中的梯度更新——训练过程中损失函数的统计分析

在训练深度学习模型时，损失函数的变化过程直接影响模型的优化效果。为了监控训练过程，我们可以使用统计量来分析损失函数的变化趋势和波动性，从而优化学习率等超参数。

步骤1：定义损失函数

• 假设我们训练一个神经网络模型，损失函数为均方误差（MSE）：

  

步骤2：训练过程中的损失函数统计

• 在训练过程中，我们记录每个epoch（训练轮次）的损失值。假设在第1轮训练后，损失为0.5，第2轮为0.45，第3轮为0.4，以此类推。

步骤3：计算集中趋势统计量

• 均值损失：计算所有epoch的损失均值，反映训练过程中的损失趋势。

  

  假设训练进行了10轮，均值损失为0.42。

步骤4：计算离散程度统计量

• 标准差：计算损失值的标准差，衡量训练过程中损失函数的波动性。

  

  假设标准差为0.05，表示损失函数在训练过程中有一定的波动。

步骤5：调整超参数

• 如果发现损失函数波动较大，可能是学习率过大，导致训练过程不稳定。在这种情况下，可以根据标准差的变化情况适当调整学习率，从而提高训练稳定性。

---

小结

本节深入探讨了统计量在数据分析和AI应用中的重要性。通过集中趋势统计量、离散程度统计量和分布形态统计量，我们能够全面了解数据的基本特征，并据此作出有效的决策。在实际的AI应用中，无论是电商平台的用户行为分析、金融市场的风险评估，还是深度学习的模型训练，统计量都发挥着至关重要的作用。

通过具体的案例，我们展示了如何使用统计量来总结和推断数据的特性。在AI模型的训练过程中，统计量不仅帮助我们理解数据的分布，还能提供有关优化和调参的指导。掌握并灵活运用这些统计工具，将大大提升我们对数据的理解力和模型的性能。