机器学习练习二：多元线性回归

    <div class="markdown_views"><hr>

转载出处：http://blog.csdn.net/and_w/article/details/52727795

作者：John Wittenauer
翻译：GreatX
源：Machine Learning Exercises In Python, Part 2

---

这篇文章是一系列 Andrew Ng 在 Coursera 上的机器学习课程的练习的一部分。这篇文章的原始代码，练习文本，数据文件可从这里获得。

Part 1 简单线性回归（Simple Linear Regression）
Part 2 多元线性回归（Multivariate Linear Regression）
Part 3 逻辑回归（Logistic Regression）
Part 4 多元逻辑回归（Multivariate Logistic Regression）
Part 5 神经网络（Neural Networks）
Part 6 支持向量机（Support Vector Machines）
Part 7 K-均值聚类与主成分分析（K-Means Clustering & PCA）
Part 8 异常检测与推荐（Anomaly Detection & Recommendation）

在 我的机器学习系列文章的第一部分，我们完成了 Andrew Ng 的 Machine Learning 练习 1 的第一部分。在本篇文章中，我们将完成 练习 1 的第 2 部分以结束整个 练习 1。如果你还记得，在第一部分，我们实现了线性回归以预测基于城市人口的食品卡车要放在哪里。在第二部分，我们有了新任务——预测房子的销售价格。这次的不同之处是我们有多个因变量——如：房子的平方英尺数和房子里的卧室数。我们能迅速的拓展我们之前的代码来处理多元线性回归吗？
让我们找出来吧！
首先，让我们看一看数据。

path = os.getcwd() + '\data\ex1data2.txt'  
data2 = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])  
data2.head()  
 
 
1
2
3
 
 

  
  
 
 
 
 
1
2
3

	Size	Bedrooms	Price
0	2104	3	399900
1	1600	3	329900
2	2400	3	369000
3	1416	2	232000
4	3000	4	539900

注意，每个变量的数值规模是截然不同的。一个房子通常有 2-5 间卧室但可能面积有从几百到几千平方英尺的。如果我们就这样的在这些数据上运用我们的回归算法，size 变量将会过重并且最终压缩“卧室数”特征的贡献。为了修正它，我们需要一个叫“特征归一化”（feature normalization）的东西。也就是说，我们需要调整特征的规模以达到同一水平。有一种方法是将一个特征中的每个值减去该特征的平均值，然后除以标准差。幸运的是，用 pandas 只需一行代码。

data2 = (data2 - data2.mean()) / data2.std()  
data2.head()  
 
 
1
2
 
 

  
  
 
 
 
 
1
2

	Size	Bedrooms	Price
0	0.130010	-0.223675	0.475747
1	-0.504190	-0.223675	-0.084074
2	0.502476	-0.223675	0.228626
3	-0.735723	-1.537767	-0.867025
4	1.257476	1.090417	1.595389

接下来，我们需要修改在第一部分中的线性回归实现以处理多个自变量。我们真的需要吗？让我们再次看看梯度下降的代码。

def gradientDescent(X, y, theta, alpha, iters):  
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X * theta.T) - y

        for j in range(parameters):
            term = np.multiply(error, X[:,j])
            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))

        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 
 

  
  
 
 
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

仔细看计算误差项的那行代码：error = (X * theta.T) - y。起初可能并不明显，但我们正在使用矩阵运算！这就是线性代数的力量。这段代码将会正确的运行不管多少变量（列）属于 X 的行数一致。最重要的是，它是一个非常高效的计算。这是一个强大的方法一下将任何表达式应用到大量的实例中。

既然我们的梯度下降和代价函数用的都是矩阵运算，事实上没有改变代码来处理多元线性回归的必要。让我们来试一试。我们首先需要执行一些初始化来创建合适的矩阵以传递给我们的函数。

# add ones column
data2.insert(0, 'Ones', 1)

# set X (training data) and y (target variable)
cols = data2.shape[1]  
X2 = data2.iloc[:,0:cols-1]  
y2 = data2.iloc[:,cols-1:cols]

# convert to matrices and initialize theta
X2 = np.matrix(X2.values)  
y2 = np.matrix(y2.values)  
theta2 = np.matrix(np.array([0,0,0])) 
 
 
1
2
3
4
5
6
7
8
9
10
11
12
 
 

  
  
 
 
 
 
1
2
3
4
5
6
7
8
9
10
11
12

现在，我们已经准备好试一试了。让我们看看会怎么样。

# perform linear regression on the data set
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)

# get the cost (error) of the model
computeCost(X2, y2, g2)  
 
 
1
2
3
4
5
 
 

  
  
 
 
 
 
1
2
3
4
5

0.13070336960771897
 
 
1
 
 

  
  
 
 
 
 
1

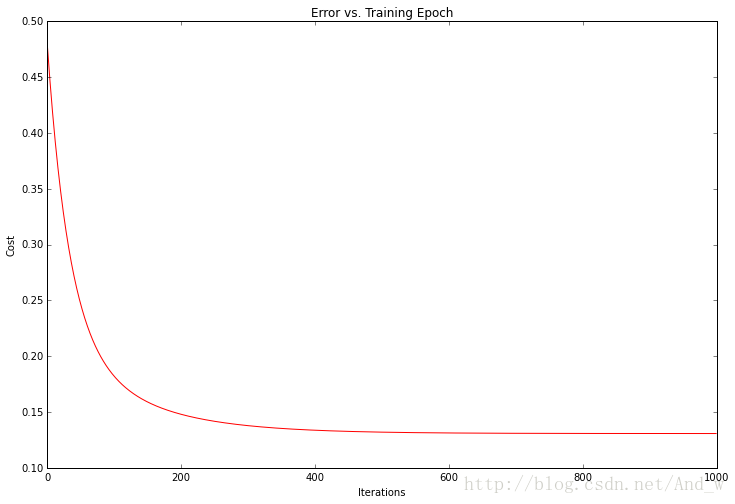
看起来不错！我们也可以绘制训练过程以确认每次梯度下降迭代后误差事实上都在下降。

fig, ax = plt.subplots(figsize=(12,8))  
ax.plot(np.arange(iters), cost2, 'r')  
ax.set_xlabel('Iterations')  
ax.set_ylabel('Cost')  
ax.set_title('Error vs. Training Epoch')  
 
 
1
2
3
4
5
 
 

  
  
 
 
 
 
1
2
3
4
5

代价函数或者解的误差，在每次成功的迭代后都下降了直到触底。这正是我们所期待的。这看起来像我们的算法运行正常。
值得注意的是，我们不必从头开始实现任何算法来解决这个问题。
Python 的一个好处是，它有庞大的开发者社区和大量的开源软件。在机器学习领域，顶尖的 Python 库是 scikit-learn 。让我们看看怎么用 scikit-learn 的线性回归类处理我们第一部分的简单线性回归任务。

from sklearn import linear_model  
model = linear_model.LinearRegression()  
model.fit(X, y)  
 
 
1
2
3
 
 

  
  
 
 
 
 
1
2
3

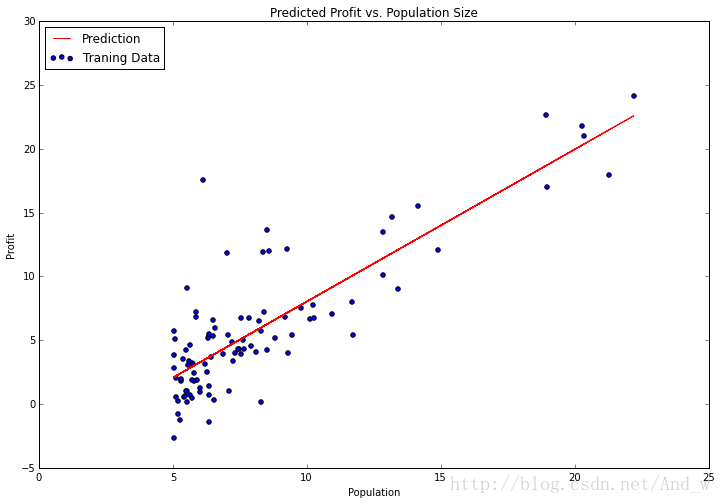
没有什么比这个更容易了。fit 方法有很多参数供我们调整，这取决于我们想要的算法功能，对于我们的问题默认的已经足够了，所以我留下了他们。让我们试着绘制拟合参数（ the fitted parameters）看看和我们之前的解有何差别。

x = np.array(X[:, 1].A1)  
f = model.predict(X).flatten()

fig, ax = plt.subplots(figsize=(12,8))  
ax.plot(x, f, 'r', label='Prediction')  
ax.scatter(data.Population, data.Profit, label='Traning Data')  
ax.legend(loc=2)  
ax.set_xlabel('Population')  
ax.set_ylabel('Profit')  
ax.set_title('Predicted Profit vs. Population Size') 
 
 
1
2
3
4
5
6
7
8
9
10
 
 

  
  
 
 
 
 
1
2
3
4
5
6
7
8
9
10

注意：为了画出这条线，我使用了 predict 函数来获取预测的 y 值。这比试图手动设置更容易。Scikit-learn 有十分优秀的 API 对典型的机器学习工作流提供很多便捷的函数。在以后的文章里我们将更仔细地研究其中的一些。

今天就这么多。在第三部分，我们将看看 练习 2 并且用逻辑回归的方法进行一些分类任务。

---