分治法算法

笙念&

已于 2022-12-22 13:00:38 修改

阅读量1k

点赞数 4

分类专栏：算法---基础算法文章标签：算法 c语言排序算法 c++

于 2022-12-22 11:48:32 首次发布

本文链接：https://blog.csdn.net/lclchong/article/details/128405907

版权

算法---基础算法专栏收录该内容

22 篇文章 7 订阅

订阅专栏

一算法简介

①算法定义

分治是广为人知的算法思想。当我们遇到一个难以直接解决的大问题时,自然会想到把它划分成一些规模较小的子问题,各个击破，“分而治之(Divide and Conquer)” 分治算法的具体操作是把原问题分成 k 个较小规模的子问题,对这 k 个子问题分别求解。如果子问题不够小,那么把每个子问题再划分为规模更小的子问题。这样一直分解下去,直到问题足够小,很容易求出这些小问题的解为止。

②算法特征

分治法的题目，需要符合两个特征：

（1）平衡子问题：子问题的规模大致相同。能把问题划分成大小差不多相等的k个子问题，最好k＝2，即分成两个规模相等的子问题。子问题规模相等的处理效率，比子问题规模不等的处理效率要高。

（2）独立子问题：子问题之间相互独立。这是区别于动态规划算法的根本特征，在动态规划算法中，子问题是相互联系的，而不是相互独立的。

需要说明的是,分治法不仅能够让问题变得更容易理解和解决,而且常常能大大伏化算法的复杂度,如把 O(n)的复杂度优化到 O(log2n)。这是因为局部的优化有利于全局;一个子问题的解决,其影响力扩大了 k 倍,即扩大到了全局。

一个简单的例子：在一个有序的数列中查找一个数。简单的办法是从头找到尾，复杂度是O(n)。如果用分治法，即“折半查找”，最多只需要logn次就能找到。这个方法是二分法，二分法也是分治法。

③算法编程

分治法的思想，几乎就是递归的过程，用递归程序实现分治法是很自然的。

用分治法建立模型时，解题步骤分为三步：

（1）分解（Divide）：把问题分解成独立的子问题；

（2）解决（Conquer）：递归解决子问题；

（3）合并（Combine）：把子问题的结果合并成原问题的解。

分治法的经典应用，有汉诺塔、快速排序、归并排序等。

二算法应用

汉诺塔

问题描述

汉诺塔是一个古老的数学问题:有 3根杆子 A,B;C。A 杆上有 N 个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆:每次只能移动一个圆盘;大盘不能叠在小盘上面(提示，可将圆盘临时置于 B杆,也可将从A 杆移出的圆盘重新移回 A 杆,但都必须遵循上述两条规则)。问:如何移动?最少要移动多少次?
输入: 输入两个正整数，一个是 N(N15),表示要移动的盘子数;一个是M,表示在最少移动步骤的第 M 步。
输出:共输出两行。第1行输出格式为:#No:a->b,表示第 M 步具体移动方法，其中 No表示第 M 步移动的盘子的编号(N 个盘子从上到下依次编号为1~N),表示第M 步是将No号盘子从a 杆移动到6杆(a 和b的取值均为(A、B、C))。第2行输出一个整数,表示最少移动步数。

举例：输入 3 2 输出 #2：A->B \n 7

问题解析

汉诺塔的经典解法是分治法。汉诺塔的逻辑很简单: 把 n 个盘子的问题分治成两个子问题。设有x,y、2 3 根杆子,初始的 n 个盘子在 x杆上。

(1) 把 x杆的 n-1个小盘移动到 y (把这 n-1 个小盘看做一个整体),然后把第 n个大盘移动到 z杆;
(2)_把y杆上的 n-1 个小盘移动到z杆

分析代码复杂度。每次分治，分成两部分，以两倍递增：一分二，二分四。。。。复杂度为O(2的n次方），在汉诺塔中，分治法不能降低复杂度

问答解答

#include<stdio.h>
int sum = 0, m;
void hanoi(char x,char y,char z,int n){  //三个柱子x、y、z
    if(n==1) {                           //最小问题
        sum++;
        if(sum==m) 
        	printf("#%d:%d->%d",n,x,z);
    }
    else {                               //分治
        hanoi(x,z,y,n-1);    //(1)先把x的n-1个小盘移到y，然后把第n个大盘移到z
        sum++;
        if(sum==m) printf("#%d:%d->%d",n,x,z);
        hanoi(y,x,z,n-1);    //(2)把y的n-1个小盘移到z
    }
}
int main(){
    int n;    scanf("%d %d",&n,&m);
    hanoi('A','B','C',n);
    printf("%d",sum);
    return 0;
}

快速幂

问题描述

幂运算a的n次方。快速幂就是高效的算出a的n次方。当n很大时，如n等于10的九次方爆破里会超时

问题解析

先算 a的平方,然后再继续算平方(a2),再继续平(a2)),一直算到n 次幂,总共只需要算 O(logn)次.这就是分治法。另外由于a的n次方极大,一般会取模再输出。

问题解答

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;                  //注意要用long long，用int会出错
ll fastPow(ll a, ll n,ll m){           //an mod m
    if(n == 0)   return 1;             //特判 a0 = 1
    if(n == 1)   return a;
    ll temp = fastPow(a, n/2,m);       //分治
    if(n%2 == 1) return temp * temp * a % m;  //奇数个a。也可以这样写： if(n &1)        
    else    return temp * temp % m ;          //偶数个a        
}
int main(){
    ll a,n,m;   cin >> a >> n>> m;
    cout << fastPow(a,n,m);
    return 0;
}

三分治思想设计排序算法

步骤解析

（1）分解。把原来无序的数列，分成两部分；对每个部分，再继续分解成更小的两部分……在归并排序中，只是简单地把数列分成两半。在快速排序中，是把序列分成左右两部分，左部分的元素都小于右部分的元素；分解操作是快速排序的核心操作。

（2）解决。分解到最后不能再分解，排序。

（3）合并。把每次分开的两个部分合并到一起。归并排序的核心操作是合并，其过程类似于交换排序。快速排序并不需要合并操作，因为在分解过程中，左右部分已经是有序的。

归并排序

下面给出了归并排序的操作步骤。初始数列经过 3 次归并之后,得到一个从小到大的有序数列。请根据这个例子,自己先分析它是如何实现分治法的分解、解决、合并3 个步骤的

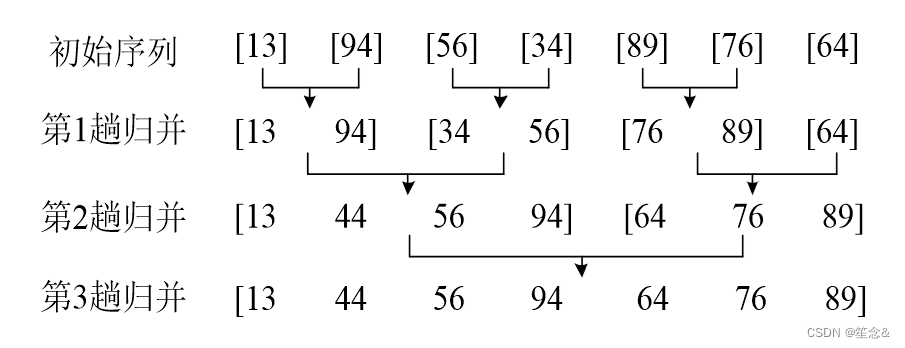
归并排序的主要操作

(1)分解。把初始序列分成长度相同的左右两个子序列,然后把每个子序列再分成更小的两个子序列,直到子序列只包含一个数。这个过程用递归实现,上图第 1行是初始序列,每个数是一个子序列,可以看成递归到达的最底层。

(2) 求解子问题,对子序列排序。最底层的子序列只包含一个数,其实不用排序。

(3)合并。归并两个有序的子序列,这是归并排序的主要操作,过程如下图所示例如,下图(a)中,和;分别指向子序列(13,94,99)和(34,56)的第 1个数,进行第 1次比较,发现 a[]<a[],把 a[]放到临时空间 6[]中。总共经过 4 次比较,得到 6](13,34，56，94，99}

复杂度分析

对n个数进行归并排序：

1）需要logn趟归并；

2）在每一趟归并中，有很多次合并操作，一共需要O(n)次比较。

所以时间复杂度是O(nlogn)。

空间复杂度：需要一个临时的b[]存储结果，所以空间复杂度是O(n)。

从归并排序的例子，读者可以体会到，对于整体上O(n)复杂度的问题，通过分治，可以减少为O(logn)复杂度的问题。

归并排序与交换排序

交换排序的步骤：

1）第一轮，检查第一个数a1。把序列中后面所有的数，一个一个跟它比较，如果发现有一个比a1小，就交换。第一轮结束后，最小的数就排在了第一个位置。

2）第二轮，检查第二个数。第二轮结束后，第2小的数排在了第二个位置。

3）继续上述过程，直到检查完最后一个数。

•交换排序的复杂度是O(n2)。

•在归并排序中，一次合并的操作，和交换排序很相似。只是合并的操作，是基于2个有序的子序列，效率更高。

归并算法的应用：逆序对问题

问题描述

输入一个序列{a1, a2, a3,…, an}，交换任意两个相邻元素，不超过k次。交换之后，问最少的逆序对有多少个。

序列中的一个逆序对，是指存在两个数ai和aj，有ai > aj且1≤i<j≤n。也就是说，大的数排在小的数前面。

输入：第一行是n和k，1 ≤ n ≤ 105，0 ≤ k ≤ 109；第二行包括n个整数{a1, a2, a3,…, an}，0≤ ai ≤109。

输出：最少的逆序对数量。

Sample Input：

3 1

2 2 1

Sample Output：

问题解析

当k = 0时，就是求原始序列中有多少个逆序对。

求k = 0时的逆序对，用暴力法很容易：先检查第一个数a1，把后面所有数跟它比较，如果发现有一个比a1小，就是一个逆序对；再检查第二个数，第三个数……；直到最后一个数。复杂度是O(n2)。本题n最大是105，所以暴力法会TLE。

考察暴力法的过程，会发现和交换排序很像。那么自然可以想到，能否用交换排序的升级版归并排序，来处理逆序对问题？

观察上一个图的合并过程，可以发现能利用这个过程记录逆序对，观察到以下现象：

(1) 在子序列内部,元素都是有序的,不存在逆序对; 逆序对只存在于不同的子序列之间。
(2)合并两个子序列时,如果前一个子序列的元素比后面子序列的元素小,那么不产生逆序对,如图所示;如果前一个子序列的元素比后面子序列的元素大,就会产生逆序对,如图所示。不过,在一次合并中,产生的逆序对不止一个,如在图中把 34 放到6[]中时,它与 94 和 99 产生了两个序对。体现在下面的代码中是第 10 行的cnt+=mid-i+1.
根据以上观察,只要在归并排序过程中记录逆序对就行了。
以上解决了k=0 时原始序列中有多少个逆序对的问题。现在考虑,当k≠0 时,即把序列任意两个相邻数交换不超过 k次，逆序对最少有多少?注意,不超过次的意思是可以少于k 次，而不是一定要 k 次。
在所有相邻数中，只有交换那些逆序的,才会影响逆序对的数量。设原始序列有 cnt 个逆序对,讨论以下两种情况。

(1) 如果 cnt<=k,总逆序数量不够交换 k 次。所以k次交换之后,最少的逆序对数量为0.

(2) 如果 cnt>k,让 k 次交换都发生在逆序的相邻数上,那么剩余的逆序对为 cnt-k.

求逆序对的代码几乎可以完全套用归并排序的模板,差不多就是归并排序的裸题。下面代码中的 Mergesort()和 Merge()函数是归并排序。与纯的归并排序代码相比,只多了第 10 行的 cnt+=mid-i+1。

问题解答

#include<bits/stdc++.h>
const int N = 100005;
typedef  long  long  ll;
ll a[N], b[N], cnt;
void Merge(ll l, ll mid, ll r){
     ll i=l, j = mid+1, t=0;
     while(i <= mid && j <= r){
          if(a[i] > a[j]){
               b[t++] = a[j++];
               cnt += mid-i+1;            //记录逆序对数量
          }
          else b[t++]=a[i++];
     }
   //一个子序列中的数都处理完了，另一个还没有，把剩下的直接复制过来：
    while(i <= mid)   b[t++]=a[i++];  
    while(j <= r)     b[t++]=a[j++];
    for(i=0; i<t; i++)  a[l+i] = b[i];     //把排好序的b[]复制回a[]
}
void Mergesort(ll l, ll r){
    if(l<r){
         ll  mid = (l+r)/2;                  //平分成两个子序列
         Mergesort(l, mid);
         Mergesort(mid+1, r);
         Merge(l, mid, r);                    //合并
    }
}
int main(){
    ll n,k;
    while(scanf("%lld%lld", &n, &k) != EOF){
        cnt = 0;
        for(ll i=0;i<n;i++)  scanf("%lld", &a[i]);
        Mergesort(0,n-1);                     //归并排序
        if(cnt <= k)   printf("0\n");
        else           printf("%I64d\n", cnt - k);
    }
    return 0;
}

快速排序

快速排序的主要操作

快速排序的思路是把序列分成左、右两部分,使左边所有的数都比右边的数小; 递个过程，直到不能再分为止。
如何把序列分成左、右两部分?最简单的办法是设定两个临时空间 X、Y 和一个基准数t; 检查序列中所有元素,比 t 小的放在 X 中,比 t 大的放在Y 中。不过,其实不用这么麻烦，直接在原序列上操作就行了 ,不需要使用临时空间。
直接在原序列上进行划分的方法有很多种,下面介绍一种简单的方法

复杂度分析

每一次划分，都把序列分成了左右两部分，在这个过程中，需要比较所有的元素，有O(n)次。

如果每次划分是对称的，左右两部分的长度差不多，那么一共需要划分O(logn)次。

总复杂度是O(nlogn)。

注意：

如果划分不是对称的，左部分和右部分的数量差别很大。在极端情况下，例如左部分只有1个数，剩下的全部都在右部分，那么最多可能划分n次，总复杂度是O(n2)。

所以，快速排序是不稳定的。

一般情况下快速排序效率很高，比稳定的归并排序更好。

可以观察到，快速排序的代码比归并排序的代码简洁，代码中的比较、交换、拷贝操作很少。

快速排序几乎是目前所有排序法中速度最快的方法。STL的sort()函数，C语言的qsort（）就是基于快速排序算法的，并针对快速排序的缺点做了很多优化

快速排序的应用：求第k大数问题

求第k大的数，简单的方法是排序算法进行排序，然后定位第k大的数，复杂度是O(nlogn)。

如果用快速排序的思想，可以在O(n)的时间内找到第k大的数。在快速排序程序中，每次划分的时候，只要递归包含第k个数的那部分就行了。

问题描述

给出n个数（n为奇数）以及n个数字，找到中间数

问题解答

#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 10010;
int a[N];                   //存数据
int quicksort(int left, int right, int k){
    int mid = a[left + (right - left) / 2];
    int i = left, j = right - 1;
    while(i <= j){
        while(a[i] < mid) ++i;
        while(a[j] > mid) --j;
        if(i <= j){
            swap(a[i], a[j]);
            ++i;--j;
        }
    }
    if(left <= j && k <= j) return quicksort(left, j + 1, k);
    if(i < right && k >= i) return quicksort(i, right, k);
    return a[k];                      //返回第k大数
}
int main(){
    int n;     scanf("%d", &n);
    for(int i = 0; i < n; i++)    scanf("%d", &a[i]);
    int k = n/2;
    printf("%d\n", quicksort(0, n, k));
    return 0;
}

算法拓展：减治法

减治法的题目常常被归纳到其他算法思想中。
用减治法解题的过程是把原问题分解为小问题,再把小问题分解为更小的问题,直到得到解。规模为 n 的原问题与分解后较小规模的子问题，它们的解有以下关系:

(1)原问题的解只存在于其中一个子问题中;
(2) 原问题的解和其中一个子问题的解之间存在某种对应关系

按每次迭代中减去规模的大小把减治法分成以下 3 种情况:

(1)减少一个常数，在算法的每次迭代中,把原问题减少相同的常数个，这个常数一般等于1。相关的算法有插入排序、图搜索算法(DFS、BFS),拓扑排序、生成排列、生成子集等。在这些问题中,每次把问题的规模减少 1。

(2) 按比例减少。在算法的每次迭代中,问题的规模按常数成倍减少，减少的效率极高。在大多数应用中,此常数因子等于 2。折半查找(Binary Search)是最典型的例子,在个有序的数列中查找某个数 k,可以把数列分成相同长度的两半,然后在包含 k 的那部分继续折半,直到最后匹配到k,总共只需要 logn 次折半。

(3) 每次减少的规模都不同。减少的规模在算法的每次迭代中都不同,例如查找中位数(用快速排序的思路)、插值查找，欧几里得算法等

附录：

笙念&

关注

4
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
分治法算法

①算法定义分治是广为人知的算法思想。当我们遇到一个难以直接解决的大问题时,自然会想到把它划分成一些规模较小的子问题,各个击破，“分而治之(Divide and Conquer)” 分治算法的具体操作是把原问题分成 k 个较小规模的子问题,对这 k 个子问题分别求解。如果子问题不够小,那么把每个子问题再划分为规模更小的子问题。这样一直分解下去,直到问题足够小,很容易求出这些小问题的解为止。②算法特征分治法的题目，需要符合子问题的规模大致相同。
复制链接

扫一扫