棋盘覆盖--分治法

问题：

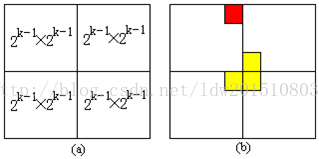
在一个2^k×2^k （k≥0）个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为特殊方格。显然，特殊方格在棋盘中可能出现的位置有4^k种，因而有4^k种不同的棋盘，棋盘覆盖问题（chess cover problem）要求用L型骨牌覆盖给定棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

思路：分治法

每次将棋盘分成四等份，特殊方格一定在其中一份里，其余三份中按照图中方法添加一块L型骨牌，因此，四份中都存在特殊方格；按此方法，递归求解即可解除。

代码：

#include<cstdio>
const int maxn = 32+2;
int Board[maxn][maxn];
int tile = 0;

void ChessBoard(int tr,int tc,int dr,int dc,int size){
	if(size <= 1)return ;
	int s = size/2;
	int t = ++tile;
	
	//覆盖左上角 
	if(dr<s+tr && dc<s+tc){
		ChessBoard(tr,tc,dr,dc,s);
	}
	else{
		Board[tr+s-1][tc+s-1] = t;
		ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
	}
	
	//覆盖右上角
	 if(dr<s+tr && dc>=s+tc){
	 	ChessBoard(tr,tc+s,dr,dc,s);
	 }
	 else{
	     Board[tr+s-1][tc+s]=t;
		 ChessBoard(tr,tc+s,tr+s-1,tc+s,s); 
	 } 
	 
	 //左下角
	 if(dr>=s+tr && dc<s+tc){
	 	ChessBoard(tr+s,tc,dr,dc,s);
	 } 
	 else {
	 	Board[tr+s][tc+s-1]=t;
	 	ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
	 }
	 
	 //右下角
	 if(dr>=tr+s && dc>=tc+s){
	 	ChessBoard(tr+s,tc+s,dr,dc,s);
	 } 
	 else{
	 	Board[tr+s][tc+s]=t;
	 	ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
	 }
}


int main(){
    Board[0][0] = 0;
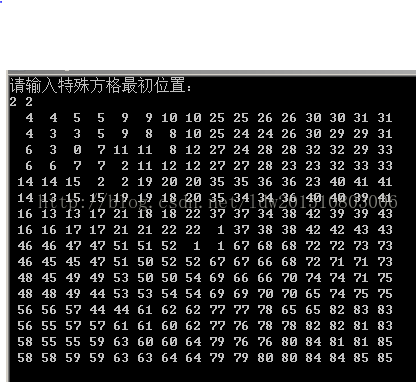
    printf("请输入特殊方格最初位置：\n");
    int dr,dc;
    scanf("%d%d",&dr,&dc);
	ChessBoard(0,0,dr,dc,16);
	for(int i = 0; i < 16; i++){
		for(int j = 0; j < 16; j++){
			printf("%3d",Board[i][j]);
		}
		printf("\n");
	}	
	return 0;
}

输出：