Matlab中极值I型分布(Gumbel分布)的evcdf和evpdf及evinv函数

此文回答

MATLAB中，极值I型分布(Gumbel)的函数evpdf和evcdf要如何使用？

进行概率运算有用到最大值型的极值I型分布（Gumbel分布），此分布函数表达式相当复杂，如下所示

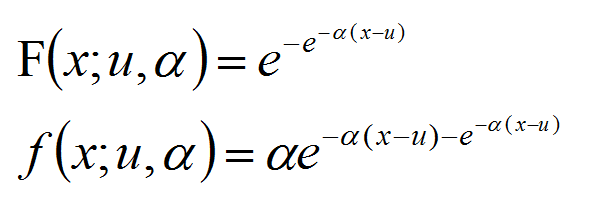
所以回答前面说的问题，mu和sigma是随机变量的均值和标准差，但并不是Matlab中的参数，Matlab里参数是分布函数和密度函数中的u和alpha。

在Matlab里有evcdf、evpdf、evinv分别表示Gumble分布的累计函数、密度函数和逆函数，和上文列出的表达式不同的是，由于Matlab里这三个函数是计算最小值型极值I型分布的。所以在调用函数时应当注意参数。

首先看极值统计学中的对称性原理：

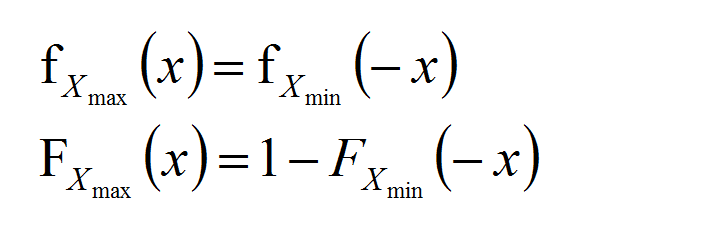
所以，evcdf等函数应参照下图等式右边使用！

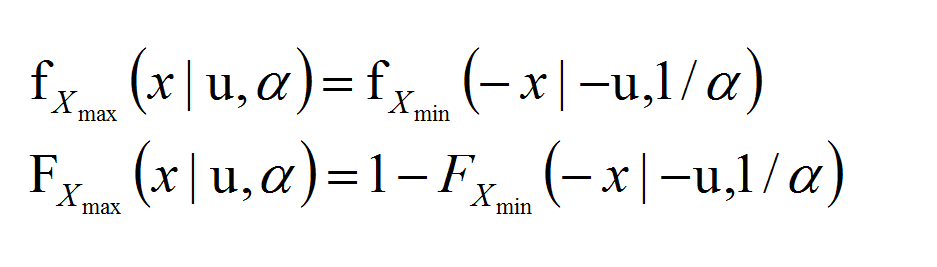
下面以前文里的问题为例说明。

书上题目：The variable Q follows an extreme Type I distribution with mu=100 and sigma=12.
Calculate FQ(150) and fQ(150).
书上答案是：FQ(150)=0.997  fQ(150)=2.86e-4.

先求-u和1/alpha

mu=100;sigma=12;

aEv=sqrt(6)*sigma/pi; <span style="white-space:pre">	</span>%aEv表示1/alpha
uEv=-psi(1)*aEv-mu;<span style="white-space:pre">		</span>%uEv表示-u,-psi(1)表示欧拉常数

FQ=1-evcdf(-150,uEv,aEv)

FQ =


    0.9973

fQ=evpdf(-150,uEv,aEv)


fQ =


  2.8589e-004

 

同理，evinv函数利用形式也稍有不同。

p=1-evcdf(-x,uEv,aEv);

x=-evinv(1-p,uEv,aEv);