3.0 序言
(1)机器学习三要素
1.模型:反映了输入数据和输出数据之间的关系(如线性的,非线性的),通常根据具体问题的经验和统计数据的分布,来假设模型。
2.策略:根据某个特定的评价标准,确定选取最优模型的策略。(通常会产出一个“损失函数”) (如使用均方误差作为线性回归的标准)
3.算法:求解损失函数,确定最优模型。(如通过最小二乘法和极大似然估计法求解ω和b的值)
(2)线性模型
基本形式:
向量形式:
(3)序关系(针对于离散属性)
若属性值之间具有“序”的关系,则需要将离散数据连续化。如:二维属性胖瘦,都是衡量人体型的指标,有一定的强弱程度,则可将“胖”“瘦”转化为{1.0, 0.0}。
若属性之间不存在对应的“序”关系,则用k维向量来表示k个属性。如:黄色,蓝色,紫色,它们之间没有谁强谁弱的程度,则它们的取值可分别化为(1, 0, 0),(0, 1, 0),(0, 0, 1)。
优点:形式简单,易于建模;有很好的“可解释性”,可通过每个维度前的系数来确定属性的重要程度。(若求得模型为:中,则
所代表的属性更加重要)
3.1 一元线性回归
(1)模型:试图学得,使得
(2)策略:最小二乘法——使得均方误差最小化,让所有样本到直线模型上的欧氏距离最小,即:

即使最小。
*拓展:使用概率论中极大似然估计法求和
的最小值:
1.假设模型,
为不受控制的随机误差,依据经验设其服从
的正态分布。
2.的概率密度函数为:

3.将用
替换得到:
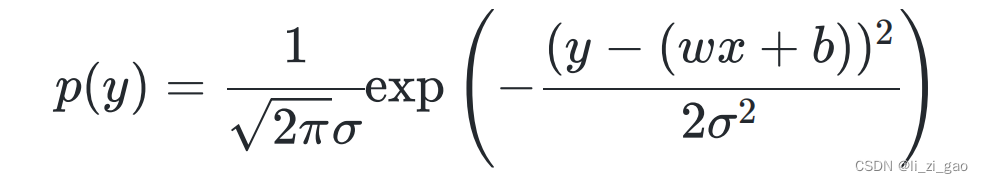
4.求解极大似然函数:
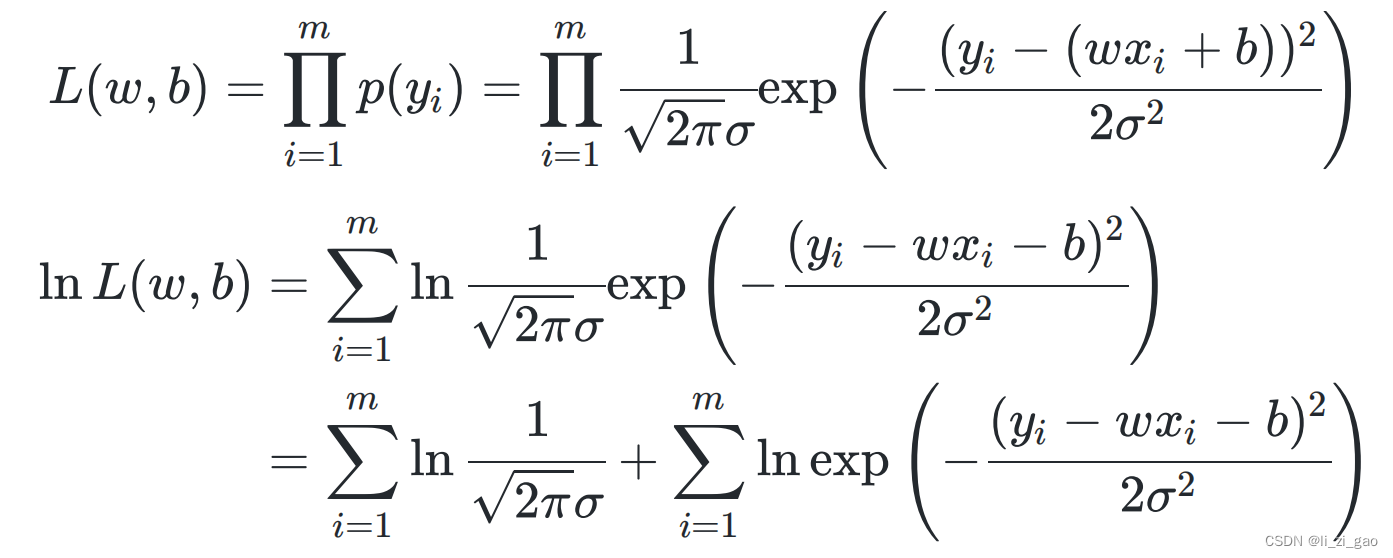

5.由于都是常数,若使
最大,则等价于使
最小。
最终,该方法与(2)中最小二乘法推出的损失函数殊途同归。
除微积分,线代,概率论外,所需补充的一些数学知识:
1)凸函数
定义:若在区间 [a,b] 上,函数 f 在此区间上的两点 x1、x2,满足 f( (x1 + x2) / 2 ) <= ( f(x1) + f(x2) ) / 2,则称 f 为区间 [a,b] 上的凸函数。(如二次函数)
判定方法:若某个函数的海塞矩阵是半正定的,则其为凸函数。
性质:若
是凸函数,且
一阶连续可微,则
是全局解
:即梯度,指多元函数的一阶导数。
2)海塞矩阵
定义:设n元函数对自变量
=
的各分量
的二阶偏导数
都存在,则称f(x)在
处二阶可导,并称下图所示矩阵为该函数的海塞矩阵。

性质:若
二阶可微,且其海塞矩阵是半正定的,则其在定义域上为凸函数。
(半正定矩阵的判定:该矩阵为实对称矩阵,且顺序主子式均为非负。)
(3)算法:
求解最小值的思路:
1:由于求解和
的问题本质上属于多元函数求最值(点)的问题,我们需证明该函数属于凸函数。
2:用凸函数求最值的方法解出其最小值。
证明过程:(过程可理解,最重要的是要记住结果)
(1)分别求二阶偏导:
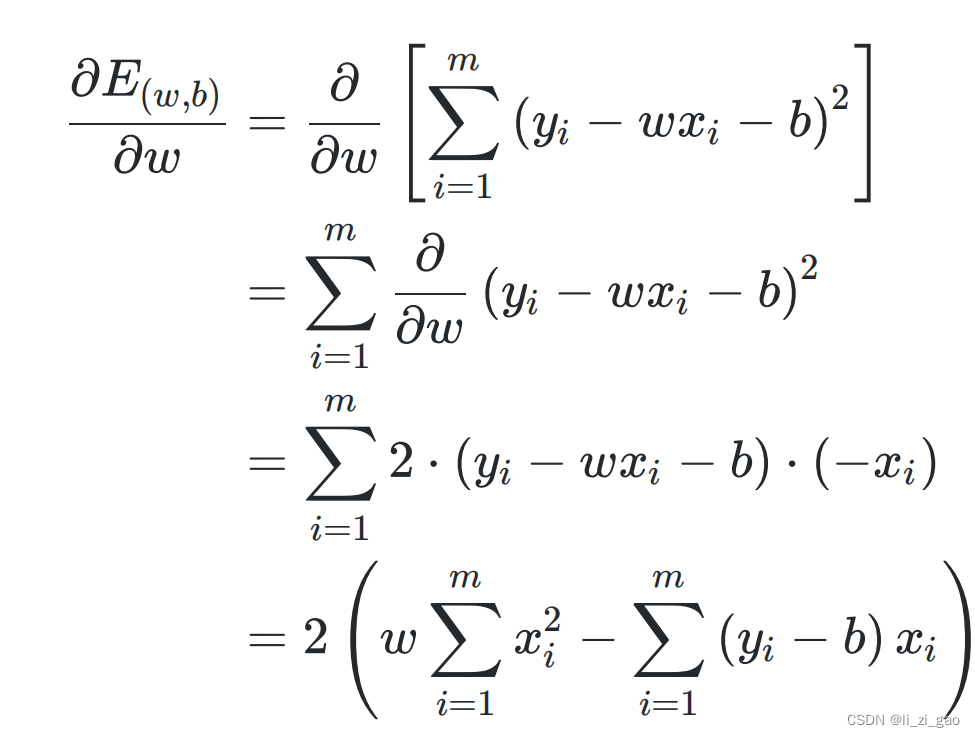
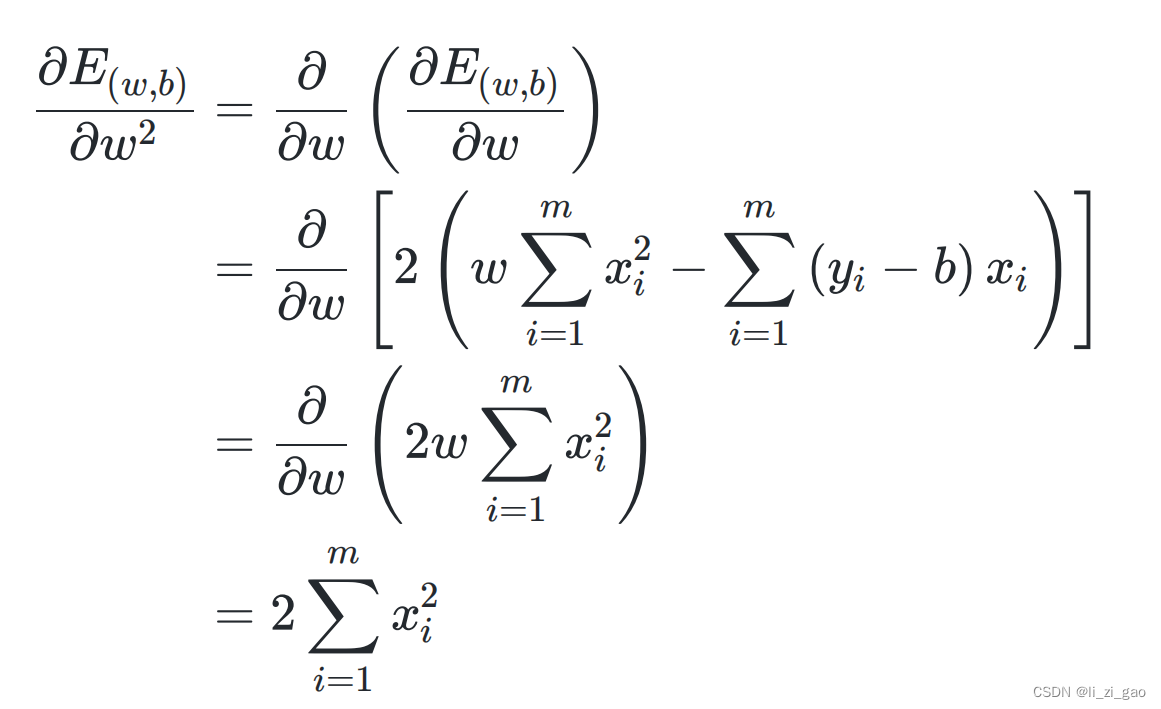


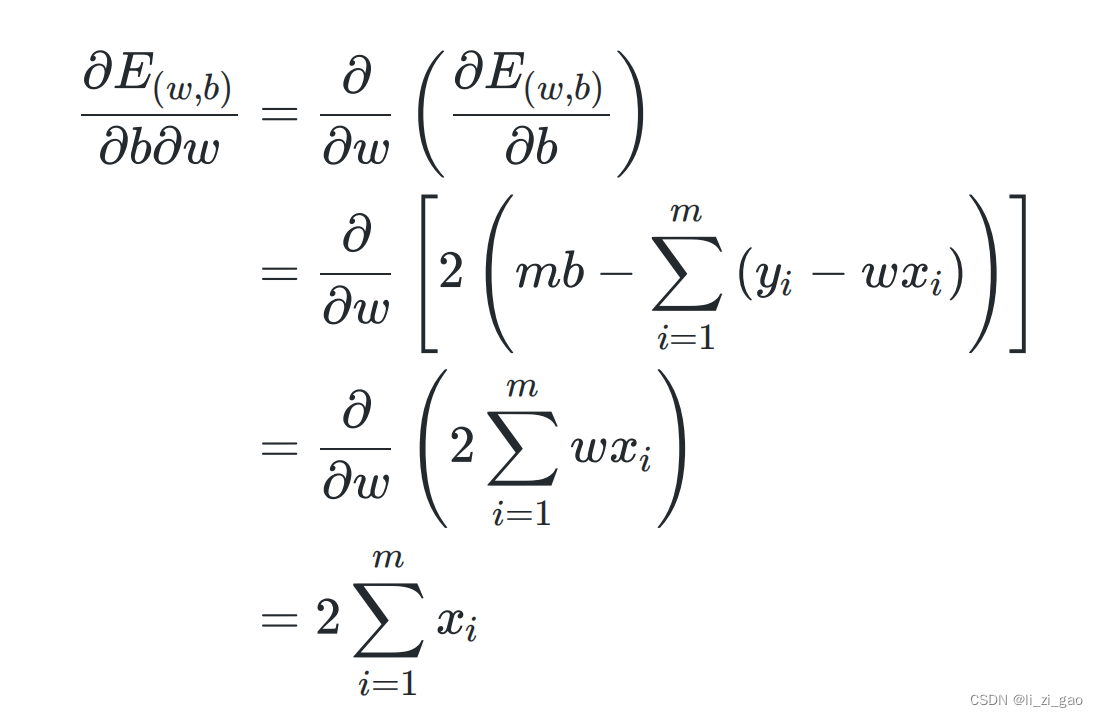
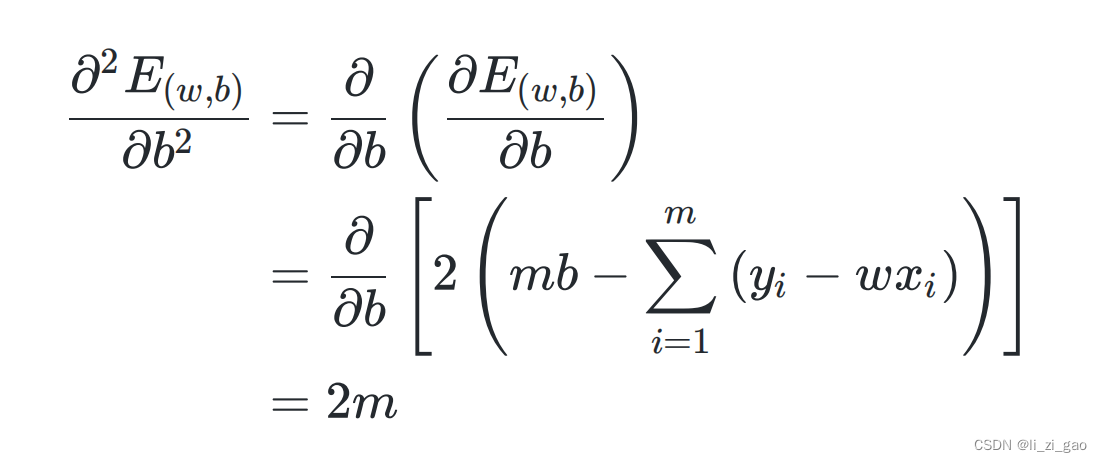
(2)列出其海塞矩阵,证明一二阶顺序主子式为非负:



(3)证明得该函数为凸函数,令其一阶偏导分别等于0,求得和
:
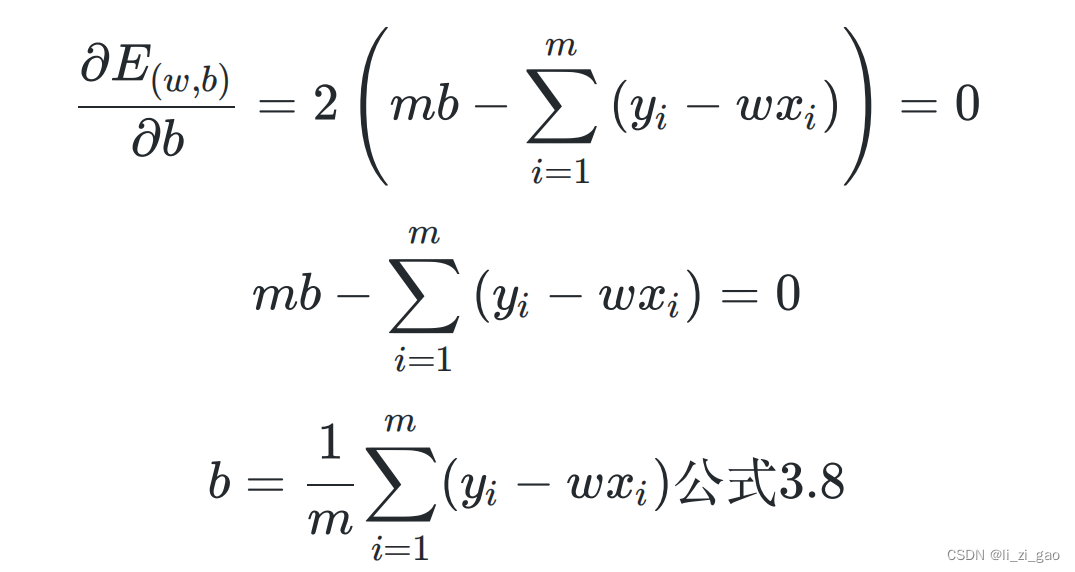






最终得到最重要的结论:和
最优解的闭式解:


3.2 多元线性回归
(1)模型:样本由d个属性描述,试图学得,使得
。
(2)最小二乘法步骤:
1. 为了消去常数项,将
和
组合成
(拓展向量维度):


2. 使用最小二乘法得到:

整理化简得:
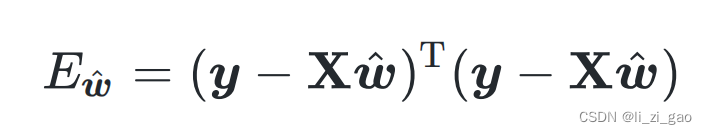
3. 用同样的思路求解(判别其海塞矩阵是否有半正定性,利用凸函数性质求解)。关于矩阵如何求导,可参考博文:
矩阵的求导_矩阵求导_意念回复的博客-CSDN博客,最终可得:
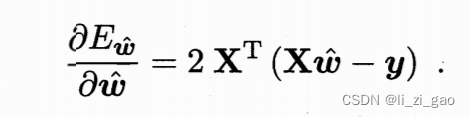
令上式为0得:

此处我们假设是满秩矩阵或正定矩阵。(否则无法得出凸函数的最小值证明)。
若不满足以上性质,则可解出多个
,此时由学习算法的归纳偏好决定输出哪个解。
最终学得得多元线性回归模型为:

3.3 对数几率回归
(1)模型:线性模型,输出值的范围为[0, 1],近似阶跃的单调可微函数
1. 回归与分类的区别:回归预测具体的数值,一般在一段范围之内;分类输出的结果是离散的,是物体所属的类别。
针对分类任务,由于线性回归模型主要针对的是连续型y值,通常没有办法借助该类模型解决问题。但只要我们找一个单调可微的映射函数,便可使线性回归得出的值化为分类问题的值。
如在线性回归模型中,
是实值,我们需要将其转化为{0, 1}。形如
的对数几率函数便是一个常用的替代函数(如下图黑线所示)。

2. 优点:输出值在附近变化很陡,可近似成{0, 1}分类;连续可微。
将代入上式得:

并可将其变化为:

这里要解释一个概念:对数几率——若将y视作样本为正例的可能性,则1-y是其为负例的可能性,二者之比
称为“几率”,对“几率”取对数即为“对数几率”。
(2)策略:极大似然估计法,信息论方法
确定和
:
1. 将离散型随机变量y取值为1和0的概率分别建模为:

同多元线性回归,为了便于讨论,令,
,上式可简写为:
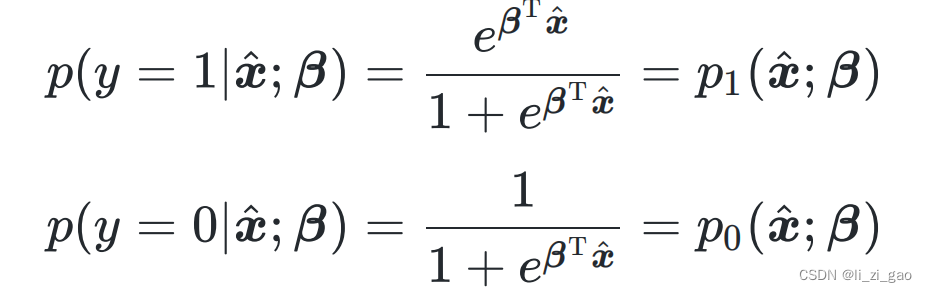
推得其概率质量函数为:
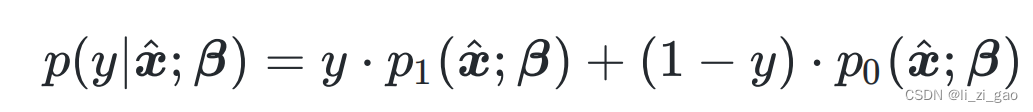
2. 写出似然函数:
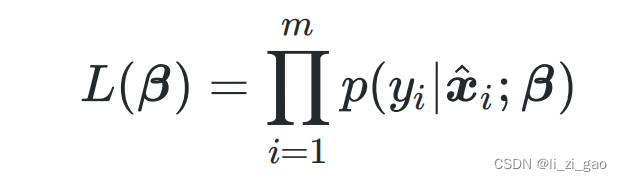
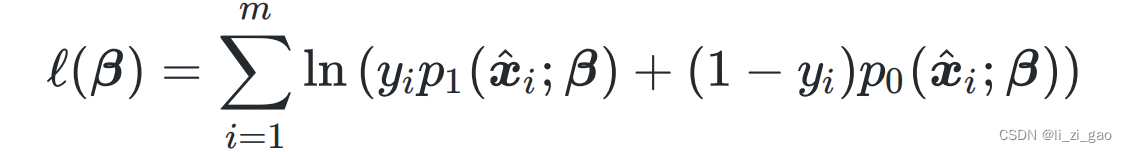


由于损失函数经常以最小化为优化目标,所以可将最大化等价为最小化
,即

(3)算法:梯度下降法,牛顿法
上式是关于的高阶可导连续凸函数,根据凸优化理论,或牛顿法,梯度下降法等可求得其最优解:

3.4 线性判别分析
(1)一些定义:数据集,
,
,
分别表示第
类示例的集合,均值向量,协方差矩阵。
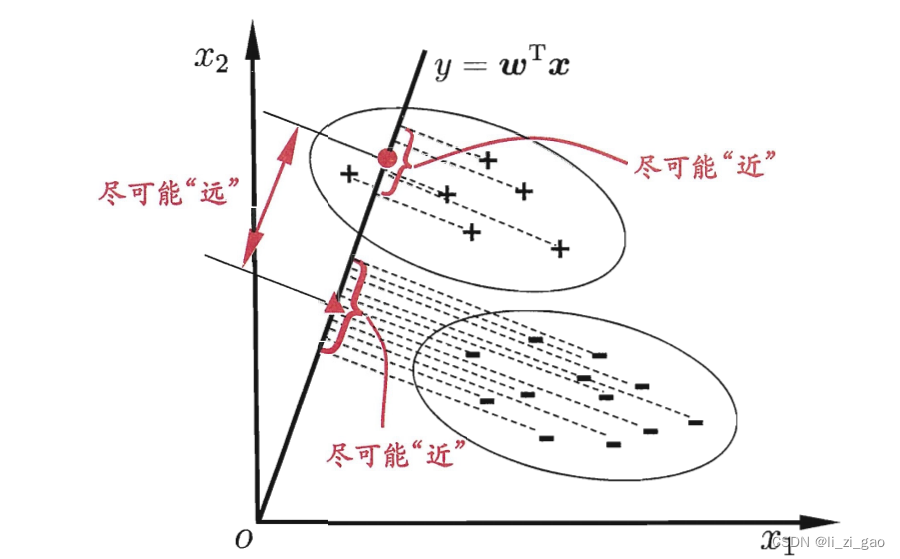
(2)本质思想:从几何角度建立的分类模型。让全体样本投影到一条直线上,使:
异类样本的中心尽可能远(二范数,表示两个均值向量在该直线上的投影差的平方,要尽可能大);
同类样本的中心尽可能近(即协方差:小,越小说明同类样本分布越均匀集中)。(如图所示)
(3)求损失函数:
通过如上思想,得到欲最大化的目标:
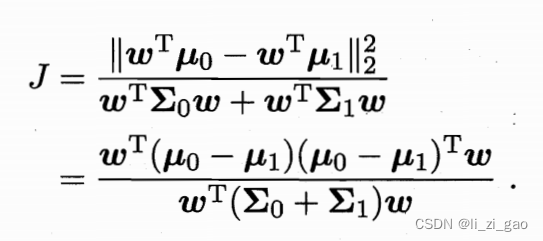
定义两个新变量(类内散度矩阵),
(类间散度矩阵),


得:
(4)求解的取值:
由于该式下分子和分母都是关于的二次项,因此该取值与
长度无关,只与其方向有关。
可使用拉格朗日乘子法:

该式子通过调整的取值,使得分母的值恒为1;又损失函数经常以最小化为优化目标,而此时目标是求J的最大值,通过给分子加负号,可使其变求最小值的形式。
得拉格朗日函数:

对求偏导可得:

又均为实对称矩阵(
:任意一个向量乘其转置是实对称矩阵,
:由协方差矩阵的定义可得。),所以令上式为0,可得:
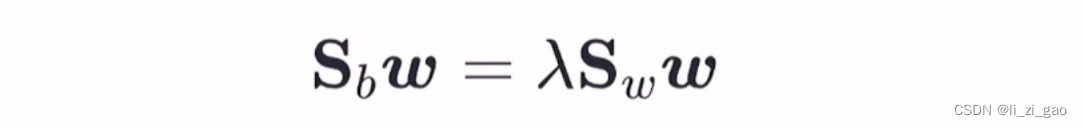
即:
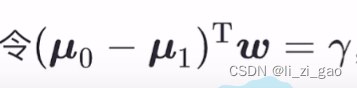
最终得到:
又对于最终求得的,不关心其大小,只关心其方向,所以其中的
可以任意取值,令
,得到最终结果:
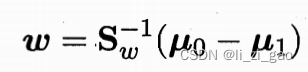
本文参考资料:
《机器学习》周志华著,清华大学出版社。






















 318
318











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








