【减法网络】Minusformer：通过逐步学习残差来改进时间序列预测

摘要

本文发现泛在时间序列(TS)预测模型容易出现严重的过拟合。为了解决这个问题，我们采用了一种去冗余的方法来逐步恢复TS的真实值。具体来说，我们引入了一种双流和减法机制，这是一种深度Boosting集成学习方法。通过将信息聚合机制从加法转向减法，对普通的Transformer进行了改造。然后，我们在原始模型的每个块中加入一个辅助输出分支，构建一条通往最终预测的高速公路。该分支后续模块的输出将减去之前学习的结果，使模型能够逐层学习监督信号的残差。这种设计促进了学习驱动的输入和输出流的隐式渐进分解，使模型具有更高的通用性、可解释性和抗过拟合的弹性。由于模型中的所有聚合都是负号，因此称为Minusformer。广泛的实验表明，所提出的方法优于现有的最先进的方法，在各种数据集上平均性能提高11.9%。

论文题目：Minusformer: Improving Time Series Forecasting by Progressively Learning Residuals
论文作者：Daojun Liang, Haixia Zhang，Dongfeng Yuan，Bingzheng Zhang 
论文地址：https://arxiv.org/abs/2402.02332 
代码地址：https://github.com/Anoise/Minusformer

论文地址
Github代码地址

图1：所提出的减速器与其他最新先进型号的比较。结果(MSE)在所有预测长度上取平均值。模型后面的数字后缀表示模型的输入长度。Minusformer配置了两个版本的输入长度，以便与其他模型保持一致。

1 简介

“在我开始工作之前，雕塑已经在大理石块内完成了。它已经存在了，我只要把多余的材料凿掉就行了。” ——米开朗基罗

在本文中，我们利用去冗余的概念提出了一种渐进式学习方法，旨在系统地获取监督信号的成分，从而提高时间序列(TS)预测的性能。在正式启动之前，让我们仔细研究一下TS预测的传统方法。

从现实世界中记录的TS由于在复杂的瞬态条件下的演化，往往表现出无数形式的非平稳性(Anderson, 1976)。非平稳TS的特征体现在不断变化的统计性质和联合分布上(Cheng et al.， 2015)，这使得准确预测变得极其困难(Hyndman and Athanasopoulos, 2018)。经典的方法如ARIMA (Piccolo, 1990)、指数平滑(Gardner Jr, 1985)和Kalman滤波(Li et al.， 2010)是基于时间序列的平稳性假设或统计性质来预测未来缺失值的，这些方法不再适用于非平稳情况(De Gooijer, 2010 and Hyndman, 2006)。

最近，由于其强大的非线性拟合能力，深度学习被引入TS预测(Hornik, 1991)，包括基于注意力的长期预测(Zhou et al.， 2021;Nie et al.， 2022;Liu et al.， 2023;Shabani et al.， 2022)或基于图神经网络(GNNs)的预测方法(Li et al.， 2018;Wu等人，2019)。然而，最新的研究表明，与多层感知器(multilayer Perceptrons, MLP)相比，使用基于注意力的方法在预测性能方面的改进并不显著(Zeng et al.， 2023;Liang等人，2023)。而且它们的推理速度相对于vanilla Transformer已经变慢了(Liang et al.， 2023)。此外，与MLP相比，基于gnn的方法在预测性能方面没有显着改善(Shao et al.， 2022)。

受前人工作的启发，我们发现流行的深度模型，例如基于transformer的模型，在TS数据上容易出现严重的过拟合。如图2所示，尽管训练损失仍在急剧下降(橙色线)，但在训练过程中过拟合发生得较早(验证损失显著增加)。尽管有许多方法可以将多变量属性嵌入到标记中(图2.a)或将单个序列嵌入到时间标记中(图2.b)，但过度拟合仍然存在。将聚合方向重新定向到时间维度，例如，基于iTransformer的模型，可以略微缓解过度拟合，但其影响受到高度限制(绿线)。因此，必须开发一种针对性的网络结构，专门用于减轻TS预测中固有的过拟合问题。

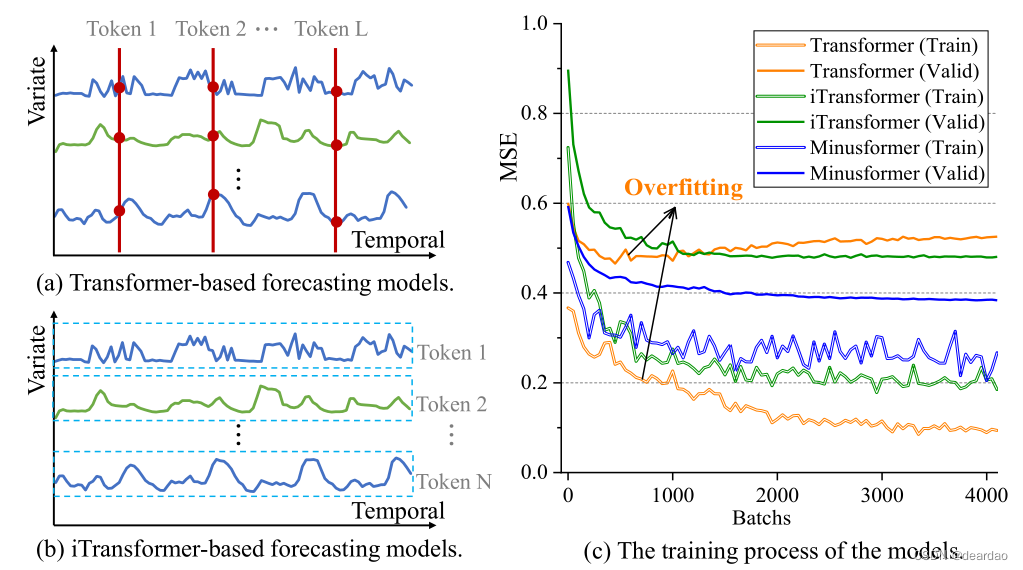
图2:时间序列在不同方向聚合时模型的概化。实验是在Traffic数据集上利用Transformer与4个块(基线)进行的。

在本文中，我们深入研究了一种去冗余方法，该方法隐式分解监督信号以逐步引导学习过程以应对过拟合问题。具体来说，我们通过修改信息聚合机制，用减法代替加法，对原有的Transformer架构进行了革新。然后，我们将辅助输出流合并到每个块中，从而构建一条通往最终预测的高速公路。该流中后续模块的输出将减去之前学习的结果，便于模型逐层渐进地学习监督信号的残差。双系统设计的结合促进了学习驱动的输入和标签的隐式渐进分解，这相当于助推集成学习(Kearns和Valiant, 1994)，从而增强了模型的通用性、可解释性和抗过拟合的弹性。考虑到所有聚合都由减号组成，这种体系结构被称为Minusformer。

此外，我们提供了基于减法的模型有效性背后的理论基础。我们证明了Minusformer中的减法可以通过逐步学习监督信号的残差来有效地减小模型的方差，从而缓解过拟合问题。最后，我们在不同领域的真实TS数据集上验证了所提出的方法。大量的实验表明，该方法优于现有的SOTA方法，在各种数据集上的平均性能提高了11.9%。

2 方法

2.1 记号

TS预测的目的是用I个历史时刻的观测值来预测$O$个未来时刻的缺失值，可以记为$Input-I-Predict-O$。若将序列的特征维记为$D$，则其输入数据可记为 X t = { s 1 t ， ⋅ ⋅ ⋅ ， s I t ∣ s t I ∈ R D } X_t = \{s^t_1，···，s^t_I| s_t^I∈R^D\} Xt​={ s1t​，⋅⋅⋅，sIt​∣stI​∈RD}。其目标标号可表示为 Y t = { s I + 1 t , ⋯   , s I + O t ∣ s I + o t ∈ R D } Y^t = \{s_{I+1}^t, \cdots, s_{I+O}^t | s_{I+o}^t \in \mathbb{R}^D \} Yt={ sI+1t​,⋯,sI+Ot​∣sI+ot​∈RD}，其中$s_i^t$是第t时刻维数为$d$的子级数。然后，我们可以通过设计一个给定输入Xt的模型F来预测${\hat{Y}}_t$，可以表示为:${\hat{Y}}_t=F(X_t)$。因此，选择合适的$F$对于提高模型的性能至关重要。为了表示简单，如果上标t在上下文中不会引起歧义，则将省略。

2.2 减法减轻过拟合

过拟合的主要原因是模型在测试集上具有低偏差和高方差(Hastie et al.， 2009)。目前，TS预测模型，尤其是深度预测模型，可以包含数百万个参数。虽然跳过连接有助于通过减轻梯度消失问题来训练更深层次的网络，但参数的数量增加了模型的复杂性，这在训练高度不稳定的TS数据集时很容易导致过拟合。我们表明，减法操作是输入和输出流的隐式分解，相当于元算法的增强，降低了模型的复杂性，从而降低了过拟合的风险。如图3所示，输入流显然是$X$的分解，因为:
$$X=\sum _{l=0}^{L-1}{f}_l(X)+$$