网格参数的应用和数学基础

引言

对于任意两个拓扑结构相似的表面，可以计算它们之间的一一对应映射。如果其中一个表面由三角形网格表示，那么计算这种映射的问题被称为网格参数化。映射到的表面通常被称为参数域。表面网格与各种域之间的参数化在计算机图形学和几何处理中有广泛的应用，如下所述。近年来，针对参数化网格的方法层出不穷，目标是不同的参数域，并侧重于不同的参数化属性。

本课程将回顾各种参数化方法，总结每种技术的主要思想，并侧重于方法的实践方面。它还提供了许多更受欢迎的方法生成的结果示例。当几种方法解决相同的参数化问题时，本综述努力基于参数化质量、效率和鲁棒性等标准提供客观比较。我们还将详细讨论从参数化中受益的应用，并讨论实施不同技术时涉及的实际问题。

1.1 应用

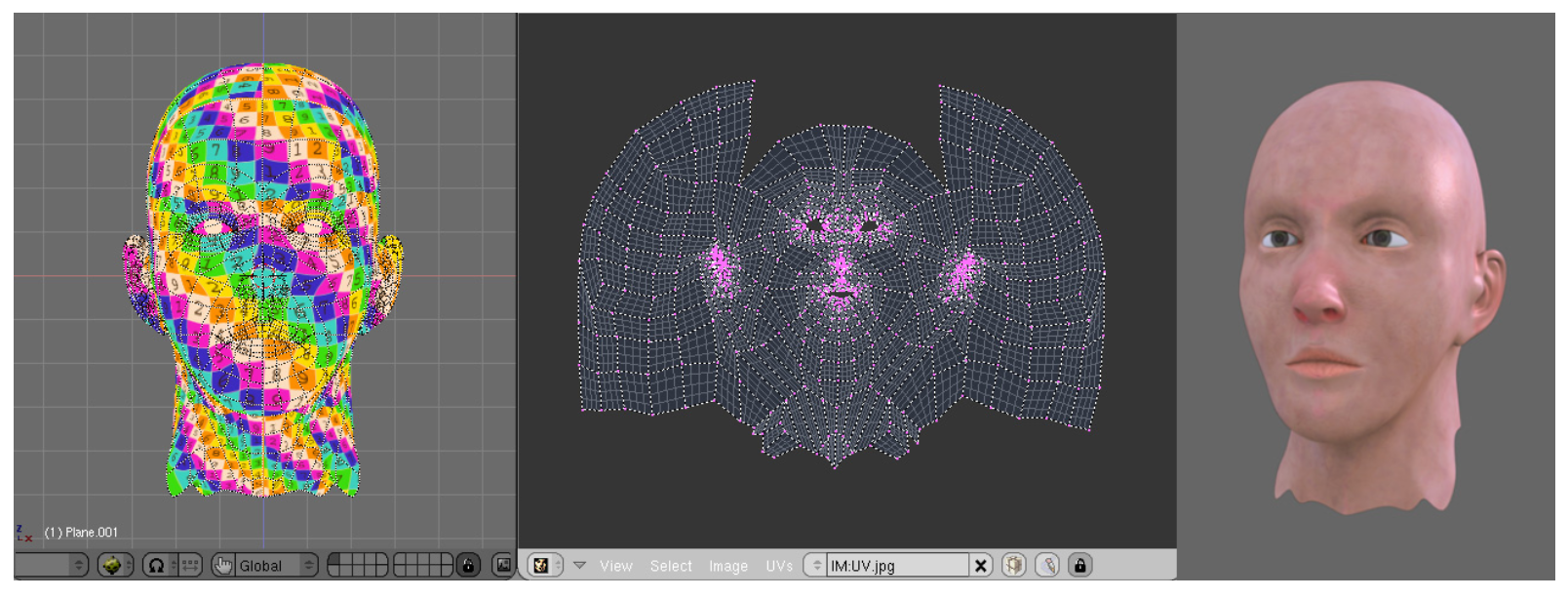
表面参数化最初作为将纹理映射到表面的方法引入计算机图形学[Bennis等人，1991年; Maillot等人，1993年]。在过去的十年中，它逐渐成为一种无处不在的工具，适用于许多网格处理应用，如下所述。

细节映射

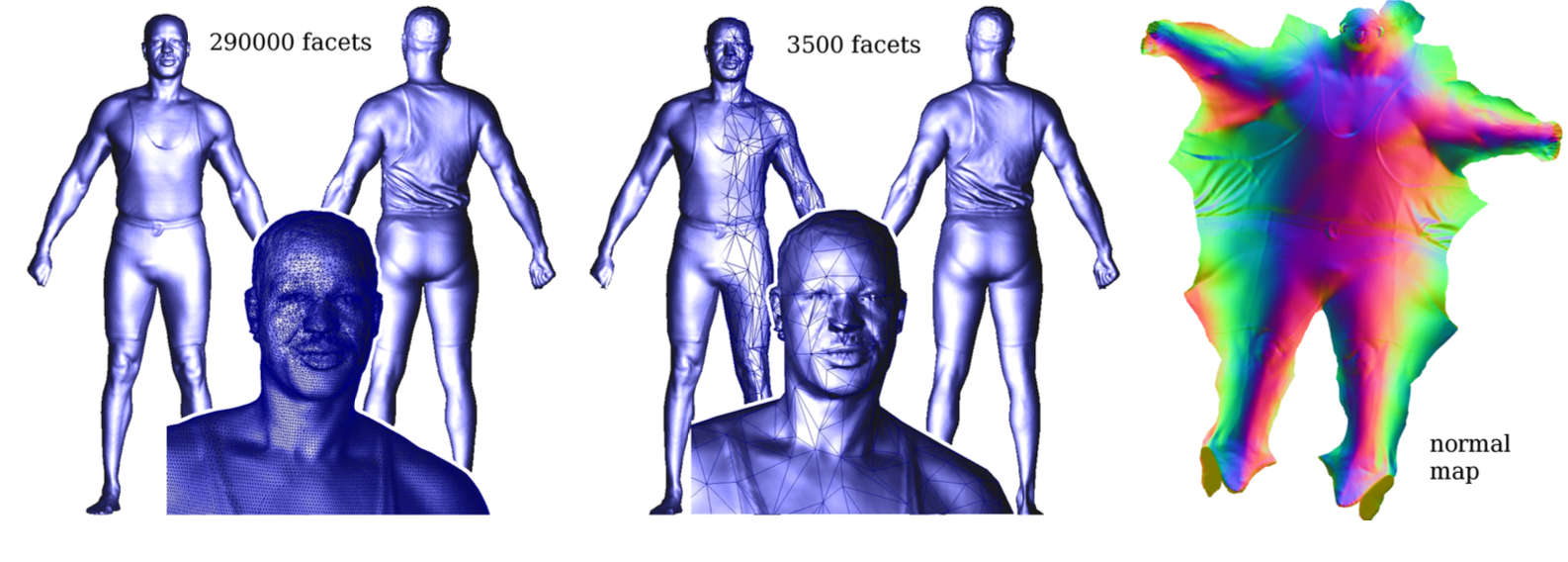
复杂的对象可以通过一个粗糙的几何形状（多边形网格或细分表面）高效表示，每个三角形对应细节存储在单独的二维数组中。在传统的纹理映射中，细节是相应像素的颜色。通过存储凹凸、法线或位移图，模型可以进一步丰富。最近的技术[Peng等人，2004年; Porumbescu等人，2005年]使用体积纹理而不是二维纹理来模拟表面附近的厚区域空间，以建模具有复杂拓扑或不易通过高度场局部近似的细节，例如稀疏交织的结构或动物皮毛。将细节映射到表面的自然方式是使用平面参数化。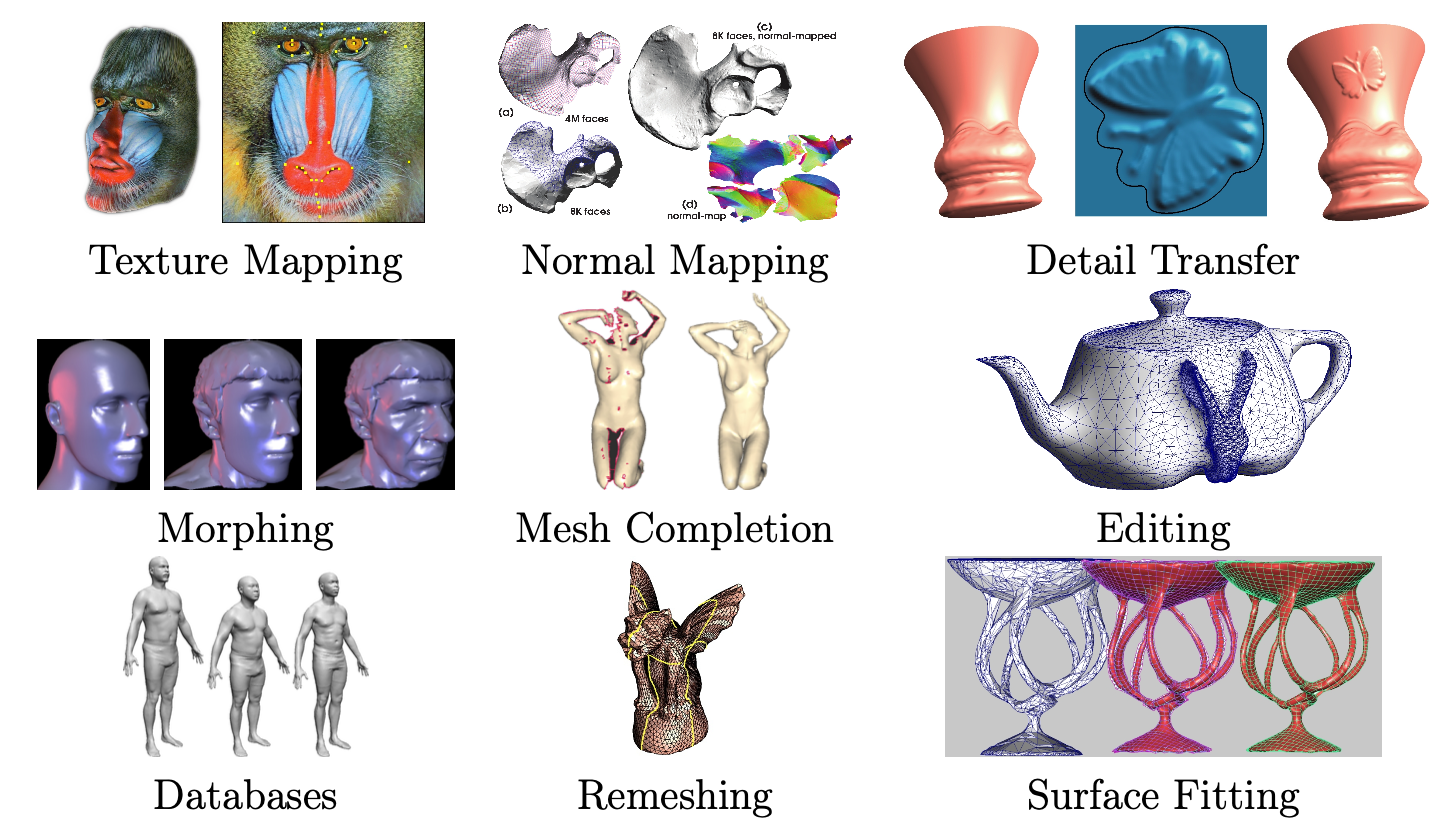

细节合成

虽然纹理映射的目标是表现3D物体的复杂外观，但有几种方法利用网格参数化来创建丰富外观所需的局部细节。这些技术可以使用平面补丁作为输入，其中包含样本细节，例如 [Soler et al., 2002]；参数化或程序化模型；或直接的用户输入和编辑 [Carr and Hart, 2004]。细节的类型可以非常多样，用于创建它的中间表示与用于存储它的最终表示相似。

变形和细节转移

两个物体表面之间的映射允许将细节从一个物体转移到另一个物体（例如 [Praun et al., 2001]），或在几个物体的形状和外观之间进行插值 [Alexa, 2000; Kraevoy and Sheffer, 2004; Schreiner et al., 2004]。通过随时间改变插值比率，可以产生变形动画。在空间变化和频率变化的变形中，物体不同部分或不同频带（被转换特征的粗细程度）的变化率可以不同 [Allen et al., 2003; Kraevoy and Sheffer, 2004]。这种映射可以直接计算，或者更常见的是通过将两个物体表面映射到一个共同的域来计算。除了转移表面的静态外观，表面间参数化还允许在形状之间转移动画数据，可以通过转移来自动画骨骼的局部表面影响，或直接转移网格中每个三角形的局部仿射变换 [Sumner and Popović, 2004]。

网格补全

来自范围扫描的网格通常包含孔洞和多个组件。Lévy [2003] 使用平面参数化来获得孔洞边界的自然形状并对其进行三角剖分。在许多情况下，关于扫描模型整体形状的先验知识是存在的。例如，对于人体扫描，通用人体形状的模板很容易获得。Allen et al. [2003] 和 Anguelov et al. [2005] 利用这种先验知识来促进扫描的补全，方法是计算扫描与模板人体模型之间的映射。Kraevoy 和 Sheffer [2005] 开发了一种更通用和稳健的基于模板的方法，用于补全任何类型的扫描。这些技术通常使用模板和扫描之间的表面间参数化。

网格编辑

编辑操作通常受益于模型对之间的局部参数化。Biermann等人[2002]使用局部参数化来促进模型之间的细节剪切和粘贴转移。他们在2D中局部参数化两个模型上的感兴趣区域，并重叠这两个参数化。他们使用参数化将形状属性从一个模型转移到另一个模型。Lévy [2003]以类似的方式使用局部参数化进行网格组合。他们计算输入模型上靠近组合边界区域的重叠平面参数化，并用它来提取和平滑混合两个模型的形状信息。

创建对象数据库

一旦大量模型在共同域上参数化，就可以进行分析，确定对象之间的共同因素和它们的区别特征。例如，在人体形状数据库中[Allen等人，2003]，区别特征可能是性别、身高和体重。可以将对象与数据库进行比较，并在这些维度上进行评分，数据库可以通过插值或外推现有对象来创建新的合理对象实例。

重新网格化

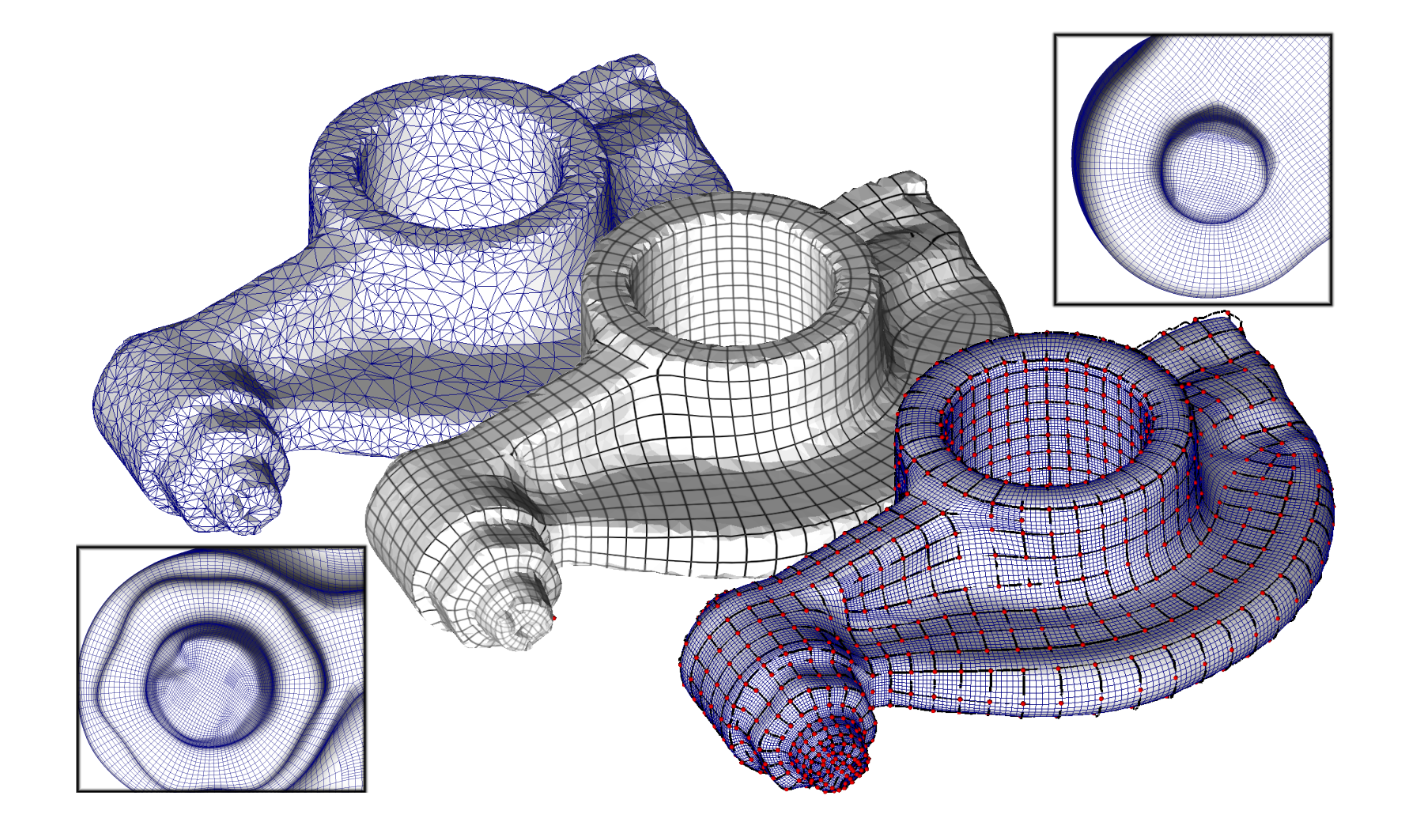
有许多可能的三角剖分可以用相似的精度水平表示相同的形状。对于不同的应用，某些三角剖分可能比其他的更理想。例如，对于表面上的数值模拟，具有良好纵横比的三角形（不太小或不太细）对于收敛性和数值精度很重要。重新网格化表面或用另一种三角剖分替换一种三角剖分的一种常见方法是参数化表面，然后将域的理想的、易于理解和创建的三角剖分映射回原始表面。例如，Gu等人[2002]使用平面正方形域的规则网格采样，而其他方法，如[Guskov等人，2000]在简单域的面上使用规则细分（通常是1比4三角形分割）。这种局部规则网格通常可以支持通过应用细分规则的极限过程创建光滑表面。为了生成高质量的三角剖分，Desbrun等人[2002]将输入网格参数化到平面中，然后使用平面Delaunay三角剖分来获得表面的高质量重新网格化。这些方法面临的一个问题是沿着为促进参数化而创建的切割线出现可见的不连续性。Surazhsky和Gotsman [2003]避免全局参数化，而是使用局部参数化作为显式重新网格化方案的一部分，在网格上移动顶点。最近的方法，如[Ray等人，2006]使用全局参数化直接在3D表面上生成以四边形为主的网格。

网格压缩

网格压缩用于紧凑地存储或传输几何模型。与其他数据一样，压缩率与数据熵成反比。因此，当模型由尽可能规则的网格表示时，无论在拓扑上还是几何上，都可以获得更高的压缩率。拓扑规则性指的是几乎所有顶点都具有相同度数的网格。几何规则性意味着三角形在形状和大小上彼此相似，且顶点接近其邻居的质心。这样的网格可以通过参数化原始对象，然后用规则采样模式重新网格化来获得[Gu等人，2002]。参数化的质量直接影响压缩效率。

表面拟合

网格参数化的早期应用之一是表面拟合[Floater，2000]。几何处理中的许多应用需要从输入网格构建平滑的分析表面。网格在基础域上的参数化显著简化了这项任务。早期方法要么将整个网格参数化到平面，要么将其分段并独立参数化每个片段。最近的方法，例如[Li等人，2006]，专注于构建平滑的全局参数化并用于拟合，实现了构建表面的全局连续性。

从材料片建模

虽然计算机图形学专注于虚拟模型，但几何处理有许多现实世界的工程应用。特别是，平面网格参数化是从材料片建模3D对象时的重要工具，范围从服装建模到金属成型或锻造[Bennis等人，1991; Julius等人，2005]。所有这些应用都需要计算平面图案以形成所需的3D形状。通常，模型首先被分割成几乎可展开的图表，然后这些图表在平面中参数化。

医学可视化

复杂的几何结构通常通过将表面法线图、颜色和其他属性映射到更简单的规范域来更好地可视化和分析。人脑是这种映射特别有用的结构之一[Hurdal等人，1999; Haker等人，2000]。大多数脑映射方法利用大脑是零亏格的事实，通过球面[Haker等人，2000]或平面[Hurdal等人，1999]参数化来可视化它。

第2章 微分几何入门

在我们详细讨论如何计算网格参数化及其应用之前，让我们快速回顾一些来自微分几何的基本性质，这些性质对于理解后面所描述的方法的动机至关重要。有关这些性质的详细信息和证明，我们建议读者参考微分几何的标准文献，特别是do Carmo [1976]、Klingenberg [1978]、Kreyszig [1991]和Morgan [1998]的书籍。

2.1 基本定义

假设Ω ⊂ R²是一个简单连通区域（即没有任何孔），例如：

• 单位正方形：Ω = {(u,v) ∈ R² : u,v ∈ [0,1]}，
• 或单位圆盘：Ω = {(u,v) ∈ R² : u²+v² ≤ 1}。

假设函数f : Ω → R³是连续且单射的（即Ω中的任何两个不同点在R³中对应的点都不同）。我们称Ω在f下的像S为一个曲面：
[ S = f(Ω) = {f(u,v) : (u,v) ∈ Ω} ]，

并称f是S在参数域Ω上的参数化。根据S的定义，f实际上是Ω和S之间的双射，因此可以定义它的逆函数f⁻¹ : S → Ω。以下是一些例子：

1. 简单线性函数：
   • 参数域：Ω = {(u,v) ∈ R² : u,v ∈ [0,1]}
   • 曲面：S = {(x,y,z) ∈ R³ : x,y,z ∈ [0,1], x+y = 1}
   • 参数化：f(u,v) = (u, 1−u, v)
   • 逆函数：f⁻¹(x, y, z) = (x, z)

2. 圆柱：

• 参数域：Ω = {(u,v) ∈ R² : u ∈ [0,2π), v ∈ [0,1]}
• 曲面：S = {(x,y,z) ∈ R³ : x² + y² = 1, z ∈ [0,1]}
• 参数化：f(u, v) = (cos u, sin u, v)
• 逆函数：f⁻¹(x, y, z) = (arccos x, z)

3. 抛物面：

• 参数域：Ω = {(u, v) ∈ R² : u, v ∈ [−1, 1]}
• 曲面：S = {(x, y, z) ∈ R³ : x, y ∈ [−2, 2], z = 4(x² + y²)}
• 参数化：f(u, v) = (2u, 2v, u² + v²)
• 逆函数：f⁻¹(x, y, z) = (x/2, y/2)

4. 半球面（正投影）：

• 参数域：Ω = {(u, v) ∈ R² : u² + v² ≤ 1}
• 曲面：S = {(x, y, z) ∈ R³ : x² + y² + z² = 1, z ≥ 0}
• 参数化：f(u, v) = (u, v, √(1 − u² − v²))
• 逆函数：f⁻¹(x, y, z) = (x, y)

定义了一个曲面S之后，我们应该注意到，函数f绝不是S在Ω上的唯一参数化。事实上，给定任何双射φ : Ω → Ω，很容易验证f和φ的复合函数，即g = f ◦ φ，也是S在Ω上的一个参数化。例如，我们可以通过定义从任何双射ρ : [0, 1] → [0, 1]轻松构造这样的重新参数化φ：

• 对于单位正方形：φ(u, v) = (ρ(u), ρ(v))
• 对于单位圆盘：φ(u, v) = (uρ(u² + v²), vρ(u² + v²))

特别地，取函数ρ(x) = 2/（1 + x），并将这种重新参数化应用于上例中半球面的参数化，得到以下替代参数化：

5. 半球面（立体投影）：

参数域：Ω = {(u, v) ∈ R² : u² + v² ≤ 1}

曲面：S = {(x, y, z) ∈ R³ : x² + y² + z² = 1, z ≥ 0}

参数化：$ f(u, v) = (\left(\frac{2u}{1 + u2 + v2}, \frac{2v}{1 + u2 + v2}, \frac{1 - u2 - v2}{1 + u2 + v2}\right)) $

逆函数：$ f⁻¹(x, y, z) = (\left(\frac{x}{1 + z}, \frac{y}{1 + z}\right)) $

这种参数化方法被称为立体投影，它具有以下特点：

1. 保角性：立体投影保持了角度，这在某些应用中非常重要。
2. 共形映射：它是一种共形映射，意味着它在局部保持形状。
3. 无奇点：除了北极点（在这个半球面的情况下是(0,0,1)）外，映射是平滑的。
4. 双有理函数：参数化和其逆都是有理函数，这在某些计算中可能有优势。

立体投影在地图制图、复分析和其他数学领域中有重要应用。它提供了一种将球面（或半球面）上的点与平面上的点进行对应的方法，这在处理球面几何问题时非常有用。

2.2 内在曲面性质

虽然曲面的参数化不是唯一的——我们将在后面讨论如何根据某些标准获得“最佳”参数化——但它仍然是一个非常方便的工具，因为它可以用来计算曲面的各种性质。例如，如果f是可微的，那么它的偏导数

$ f_u = \frac{\partial f}{\partial u} 和 f_v = \frac{\partial f}{\partial v} $

展开了局部切平面，通过简单地计算它们的叉积并归一化结果，我们得到曲面的法向量

$ n_f = \frac{f_u \times f_v}{||f_u \times f_v||} $

为了简化符号，我们常将$ ( f_u )和( f_v ) $<fo$