Stream Processing：滑动窗口的聚集（aggregation）操作的优化算法讲解

本文将要讲解流处理中滑动窗口聚集操作的相关优化算法。将分别从下面几个方面讲解：

1. 什么是滑动窗口？
2. 什么是滑动窗口的聚集操作？
3. 聚集操作的优化的必要性在哪里？
4. 有哪些优化算法，它们的原理分别是什么？
   4.1 No Pane No Gain算法
   4.2 B-Int算法
   4.3 双栈算法
   4.4 DABA（平摊式的双栈）算法
   4.5 Reactive Aggregator算法
   4.6 order statistics tree有序统计树算法

1. 什么是滑动窗口？

实时计算的流处理中，因为数据是以流的形式不断流入实时处理，把流数据保留到内存中以待以后再处理不是一个明智的选择，一般情况下是采用窗口window来缓存最近的一部分流数据，针对这部分数据处理得到结果，这个结果反映了最近所发生的事情。有多种window，包括tumble window，session window，sliding window。而sliding window算是最常用的，它的属性有window length和sliding length，前者表示窗口的大小，后者表示每一次滑动的长度。一般情况下，后者比前者小，也就是部分窗口内的元素会被计算两次。按照window length的计量单位，有按照时间单位计算，也有按照窗口中所包含的元素个数计算，分别分类为time-based window和count-based window。下图表示一个窗口大小为4，sliding大小为1的count-based窗口。

2. 什么是滑动窗口的聚集操作？

聚集操作，aggregate，不是聚类cluster，表示的是将窗口中的元素通过某种映射得到结果，该结果是窗口中的元素共同作用的结果。“某种映射”便是所谓的函数了。举一个例子，统计当前窗口中的元素个数count。另一个例子是统计当前窗口中最大的元素Max。下面列举了常见的聚集操作：

Count
Sum 
Max 
Min 
Average

这些聚集操作有着不一样的属性，常见的属性有四种，分别是可逆性，可结合性，可交换性和长度不变性。下面对它们分别解释：

• 可逆性：如果满足这个变换，则该操作是可逆的。(x ⊕ y) $⊝$ y = x。其中$⊝$ 为⊕的逆运算，或者逆函数。比如加和减为一对逆运算。
• 可结合性：x ⊕ (y ⊕z) = (x ⊕y) ⊕z，可以结合数学中的结合律来理解。
• 可交换性：x ⊕y = y ⊕ x，结合数学中的交换律来理解。
• 长度不变性：指的是一个聚集操作的结果的长度保存不变。比如count操作，结果总是一个数值。而collect操作的结果的长度在改变着。

结合上面的四个属性，我们有下面一个统计表格：

3. 聚集操作的优化的必要性在哪里？

现在很多实时计算的算法优化主要针对滑动窗口。因为很多场景下我们使用到了滑动窗口。举一个例子，统计最近两天内股票波动最大（max）的公司名字，每一分钟返回一次结果。在该例子中，window length=2天，sliding length = 1分钟，聚集函数为max。在这个操作中，系统需要将最近两天内的股票数据保存在一个窗口中，每一分钟系统需要遍历窗口来统计其中的最大值。每一次这样的聚集操作的时间复杂度为O(n) 如果窗口中的元素很多，那么对于实时处理系统而言，这将会对系统的响应速度有很大的影响。这个影响有多大？我们可以把问题极端话一点，假设window length=5天，sliding length=1秒，一个window中所缓存的数据个数为十几万，这样的窗口有一百个。这种假设情况下，这个实时处理系统将会有很大的处理延迟问题。所以，在实时处理系统的，特别是大数据的情况下，提高聚集操作的性能是很有必要的。

4. 有哪些优化算法，它们的原理分别是什么？

现在我们的问题是，怎么优化滑动窗口的聚集操作呢？有哪一些优化算法？它们的原理是什么呢？
下面将分别对下面的算法进行讲解：

1. No Pane No Gain
2. B-Int
3. 双栈
4. DABA（平摊式的双栈）
5. Reactive Aggregator
6. order statistics tree有序统计树

4.1 No Pane No Gain算法

该算法出自论文
No Pane, No Gain: Efficient Evaluation of Sliding-Window Aggregates over Data Streams ，地址为: link.
假设现在的滑动窗口为[RANGE 4 minutes，SLIDE 1 minute]，即存储最近四分钟的数据，每一分钟滑动一次，所谓的滑动，就是每一分钟将四分钟之后的数据从窗口中删除掉。下图中的上面五行分别表示一个滑动窗口在不同时间点上的状态，该算法是将整个聚合窗口分成4=(4/1)份，每一份叫做一个pane，这里有4个pane，每一个pane中都包含有不同时间到达的数据。先计算出每一个pane的聚集结果，然后叠加所有pane聚集结果，这便是no pane no pain算法的主要思路。

为了更加清晰地表述，使用下面公式化的表示方式：
假设⊕表示聚集操作，$d{1}_i$表示pane 1中的数据，$d{2}_i$表示pane 2中的数据，以此类推。pane1的聚集结果为：$R_{p1}=d{1}_1\oplus d{1}_2\oplus d{1}_3...\oplus d{1}_n$，同理计算出pane2的聚集结果为$R_{p2}$。对于整个window的聚集运算的结果为：$R_{win}=R_{p1}\oplus R_{p2}\oplus R_{p3}\oplus R_{p4}$。

上面的例子中使用的是以时间为窗口的单位。那么如果是以数据的个数为window的计量单位的话，也是相同的道理。

该算法的性能如何呢？应该在什么情况下使用该算法才有优势呢？也就是它的优缺点是什么呢？

该算法根据滑动窗口的window length和sliding length两个属性将整个窗口分成多个pane，每一次滑动的时候，只需要计算（1）最新的那一个pane的聚集结果，以及（2）合并其他三个pane的聚集结果来得到最终的结果。相比最原始的方法，这里不需要重新计算其他三个pane的聚集结果（也就是上文所说的值$R_{p2}，R_{p3}和R_{p4}$ ）。所以，从直观来看，如果一个pane所包含的数据个数越多，那么该算法越有优势。而最坏的情况是，一个pane只包含一个元素，这时候就退化成最原始的方法了，每一次窗口的聚集操作都需要遍历一次窗口中所有的元素。

这篇文章将继续上一篇，link，讲解了滑动窗口的相关基础理论。这篇文章将重点简介滑动窗口聚集操作的各个优化算法中的B-Int.

4.2 B-Int算法

B-Int，全称为short for base intervals，该算法出自论文 Resource sharing in continuous sliding
window aggregates，链接为：link。

该算法是滑动窗口聚集操作的优化算法，但是它重点放在多个滑动窗口共享上面。也就是该算法是针对多个window的，而上一篇文章讲到的no pane no gain算法只针对一个window的优化。这个便是这两个算法优化的出发点不用之处。对于这个，下面给出具体的阐述：

假设有下面三个查询：

1. Select count(*) From Stock Win[RANGE 66 ，SLIDE 17]
2. Select sum(value) From Stock Win[RANGE 55 ，SLIDE 40]
3. Select avg(value) From Stock Win[RANGE 49 ，SLIDE 2]

上面三个查询都是针对Stock数据流的聚集查询，它们的返回值和使用的窗口大小和滑动大小也不一样。针对这样的情况，B-Int算法将它们的滑动窗口变成下图所示的共享式的。在图片中，最下面一行是原始的流数据，每一个正方形代表一个数据。最下面第二行的一个长方形表示两个原始流数据的聚集的结果。所以，这一行中的一个长方形跟它下面一行的两个正方形相对应。以此类推计算出每一个行的数据。

公式化的表示方式为:
假设下面图片最下面一行的数据为：$d_1,d_2,d_3,...d_i$，⊕表示聚集操作，那么最下面第二行表示为：$b_1=d_1\oplus d_2,b_2=d_3\oplus d_4,b_3=d_5\oplus d_6,b_4=d_7\oplus d_8$。最下面第三行表示为：$t_1=b_1\oplus b_2,t_2=b_3\oplus b_4$。以此类推。

每一行使用一个数据结构队列queue作为物理存储。

这样的表示结构使得上面层次的值是处于下面层次的值的聚集结果。使得在进行聚集查询的时间复杂度减小。举一个例子，下面图片表示索引为[47, 66]之间的数据，如果要查询[49, 66]之间的聚集结果呢？只需要聚集蓝色表示的值即可。总共只有6个值。而如果采用原始的方式的话，那么总共需要遍历计算18个值。

因为下面所示的数据结构是多个查询query合并的结果，所以其最底下的窗口长度为这些query中窗口最长的那个。构建了一个这样的数据结果，共享于这些查询当中。

该算法的缺点是什么呢？很明显它需要维护多层聚集结果。需要注意的是，一个新的数据到来之后，只需要跟这个数据有关的“长方形”，而不是重新构建整个上图所示的结构。

4.3 双栈算法

这个算法的思路来源于Stackoverflow的一个问题，链接在这里link， 问题描述的是如何在O(1)的时间复杂度下实现队列的三个操作：push_rear(),pop_front() 和get_min() 。其中有一位使用两个栈的数据结构很巧妙地解决了该问题。本人曾在一篇博文中详细讲解这个算法，链接为link，并给出了Java实现源码，所以这里只结合下面这个图片简单讲解：下图中从整体上看，它是一个队列，左进右出，下图中最先进入的数字为4，整个为[1, 5, 2, 4]， 栈的顶端黄色背景的数字永远是当前栈中最小的值。当右边的栈为空的时候，讲左边栈的元素导入右边栈中。这样的话，从队列尾部加入一个新元素，和从队列头部弹出一个元素的时间复杂度为O（1），同时，获取当前队列中最小元素的时间复杂度也是O（1）. 但是，我们发现，将左边栈中的元素导入右边的时候，该操作的时间复杂度为O(n)。但是，因为该操作是间断性发生的，所以，平摊下来的话，我们还是把该算法的这三个操作记为O(1)。不管怎么样，这样给人像是在“作弊”的感觉。所以它存在一个问题，对于计算反应敏感的应用，遇到这个间断性的导转数据的时候，将会有不可接受的影响。这里举一个例子，我们在办公室里面预订了桶装水，现实中一般情况下是师傅会定期送水过来，我们每次想喝水的时候总有水喝。如果有一次我们很口渴，却发现没水了，于是乎打电话叫师傅赶紧送水过来，还需要等待，是不是很不爽？

我们回到滑动窗口的聚类算法问题上面来，下面给出来使用的算法具体思路。聚类的结果总是保存在栈顶的黄色背景的格子中，每次调用query函数的时候，只需要将两个栈顶元素做一次聚类操作即可得到最后的聚类结果。（需要注意的是，一个元素不可能同时存在两个栈中，上图中的图片可能有一点的误导性，上图只是为了理解黄色背景的元素是如何生成的，需要注意）。

4.4 DABA（平摊式的双栈）算法

我们想在双栈算法的总体思路下，如果能把这个间断导转的问题解决，那么这就是一个相对“完美”的算法了。这篇论文的作者提出了他的解决方案，论文名字为Low-Latency Sliding-Window Aggregation in Worst-Case Constant Time，他的思路是在 Okasaki’s functional queue的基础之上的拓展，做了进一步的改进。 Okasaki’s functional queue的发表了一篇论文，名字为： Simple and efcient purely functional queues and deques。Okasaki’s functional queue的实现依赖于两个东西，第一个是编程语言的自动内存回收的功能（在java中是JVM GC，在C++中可以使用c++ 11标准库中的shared_ptr自动管理对象内存），第二个是惰性计算或者说延迟计算。总体的思路是在右边的栈变为空之前就把一定数量的元素从左边的栈导入进来，而不是等到我pop front元素的时候，发现右边的栈为空，这时候才从左边栈中导转。为了理解，打个比方，假设只要厕所里有纸就总能够用一次，现在厕所里面的纸在你上厕所的时候恰好没有了，即使你可以打电话让别人送过来，也是很麻烦的，影响心情。我们希望每次上厕所的时候里面都有纸。所以，需要有人总是在快用完的时候添加厕所纸。这算是一个虽有点俗却是很恰当的例子了。

4.5 Reactive Aggregator算法

在讲Reactive Aggregator（RA）之前先讲 FAT tree，下面给出FAT树的例子图片。

现在给出8个数，分别是a[1], a[2]…a[8]。把他们都放在一棵树的叶子节点。两个叶子节点构成一颗父节点，父节点的值为两个子节点聚集的结果。比如a = a[1] ⊕ a[2], b = a[3] ⊕ a[4], e = a ⊕ b; 以这样的方式我们就构建了一颗FAT树。如果我们要更新叶子节点的值，那这棵树将有哪些变化呢？

假设我们现在更新叶子节点a[1],a[2],a[4]和a[7]的值，如上图所示，相应地红圈的节点的值也应该更新。

我们构建这样一棵树的好处便是，可以在O(1)的时间复杂度内得到这八个元素的聚集结果。而付出的代价是需要维护非叶子节点的值。

在物理内存上是如何存储这些节点的呢？我们将所有的节点按照上面图片所示数组的形式存储，之所以选择这样的数据结构，而不是使用指针的形式，是因为FAT树是节点个数固定的满二叉树，通过父节点的索引就能够直接计算出其子节点的索引。特别是在叶子节点的遍历的时候只需要遍历数组的一部分，而不是通过递归的方式查找。

上面所讲的FAT树是静态的，数据并没有具有流动性，也就是还没支持流的特征。下面所要讲到的FlatFAT树将支持流动性，也就是能够计算流数据的聚集运算。同样地，我们使用上面数组的方式来物理存储树的各个节点。另外我们还需要保存两个指针，分别是开始指针和结束指针，它们分别指向最先到来的数据和最后到来的数据，所以整个叶子节点形成了一个环状队列。如下图所示。需要注意的是，当第一个数据到来之后，往tail pointer后面插入，如果要删除一个元素，删除head pointer所指向的值，然后往后移动一位。最初的时候叶子节点的个数为0，当数据超过叶子节点的容量的时候（这里为8），需要进行FlatFAT树的扩容。

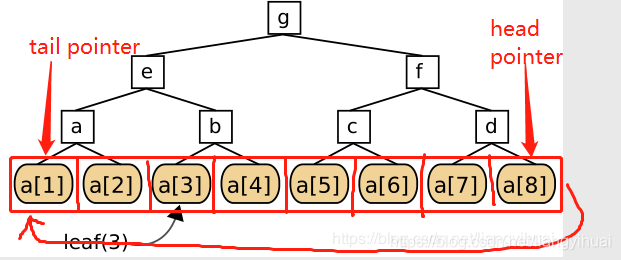
下面通过一个例子来详细讲解数据插入和清除的过程。

如上图所示，现在window的容量为4，F表示front，B表示back，分别表示两个指针，指向队列的尾部和头部元素。上面1到4行，分别插入4，7，3和2，接下来元素9到来时，因为window已经满了，所以将最老的元素4移除，将9插入队列尾部。也就是第（6）行，需要注意的是，此时B在F的前面。

那么，如何计算滑动窗口聚集结果呢？这里我们分两种情况

• 第一种是当F在B的前面，使用aggregate = a[1]⊕a[2]⊕…a[n]，也就是树的根节点的值.
• 第二种是当F在B的后面，此时顺序反过来了，聚集结果为：suffixp(F) ⊕ prefix(B)，其中
  prefix(i) = a[1]⊕a[2]⊕…a[i].
  suffix(j) =a[j]⊕…⊕a[n]. 它们分别表示两颗子树的根节点的值。

该算法的思路来自论文：General Incremental Sliding-Window Aggregation，该论文通俗易懂，推荐读一读！

4.6 order statistics tree有序统计树算法

有序统计树的作用是什么呢？

如果我们想查询窗口中前面处于k%位置的元素是什么，或者获取前面k%元素的聚类结果，我们应该怎么做呢？朴素的方法为（1）找到当前窗口中第k%元素的位置，（2）从第一个元素到第k%个元素的位置遍历，同时进行聚集运算。朴素算法的时间复杂度为O(n)。这里我们使用有序统计树来改进这种情况下的聚集运算。

有序统计树或者叫顺序统计树，是搜索二叉树的一种拓展，所以有时候为了减少最坏情况下的时间复杂度，会在平衡二叉树或者红黑树上面拓展。不管怎样，其实现原理大同小异。看下面图片，每一个节点存储两个数值，上面的值是当前节点的实际值，下面的值是size，表示当前节点的左右孩子节点的个数再加一。如何构建和维护这棵树，这里不详讲。

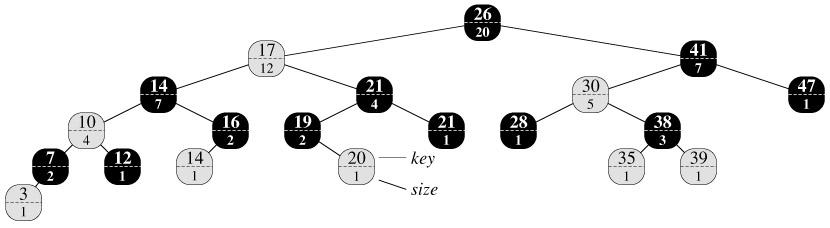
那么，如何使用上面的树来进行上面所述的聚集查询呢？比如查询窗口中后面百分之35的元素。我们知道7/20 = 0.35。所以，通过遍历该搜索二叉树，找到root节点的左左子树所在的节点，即[14, 7]。时间复杂度为O(logn)，这里n=20。

结语：

另外一篇比较新的论文Scotty: Efficient Window Aggregation for out-of-order Stream Processing，其在2018年柏林的Apache Flink Forward会议上面进行过presentation，网上可以找到相应的PPT和视频，讲得很好，未来可能会增加到Flink中，推荐了解了解！

IBM研究院发表了一篇相关的教程，类似于综述，非常推荐，链接为link，或者直接google：Tutorial: Sliding-Window Aggregation Algorithms

这篇博文通过阅读众多文献，学习各种滑动窗口聚集操作的优化算法，在此跟大家分享。谢谢！
如果觉得不错，给个赞呗！