Problem Description
“Swipe Bo” is a puzzle game that requires foresight and skill.
The main character of this game is a square blue tofu called Bo. We can swipe up / down / left / right to move Bo up / down / left / right. Bo always moves in a straight line and nothing can stop it except a wall. You need to help Bo find the way out.
The picture A shows that we needs three steps to swipe Bo to the exit (swipe up, swipe left, swipe down). In a similar way, we need only two steps to make Bo disappear from the world (swipe left, swipe up)!

Look at the picture B. The exit is locked, so we have to swipe Bo to get all the keys to unlock the exit. When Bo get all the keys, the exit will unlock automatically .The exit is considered inexistent if locked. And you may notice that there are some turning signs, Bo will make a turn as soon as it meets a
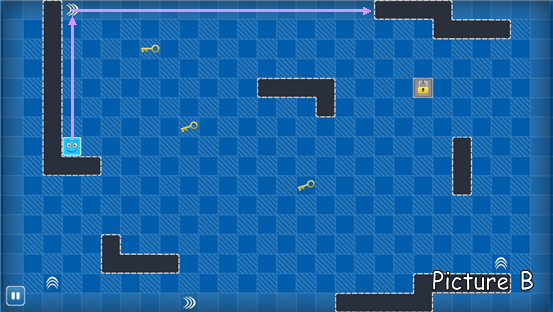
turning signs. For example, if we swipe Bo up, it will go along the purple line.
Now, your task is to write a program to calculate the minimum number of moves needed for us to swipe Bo to the exit.
The main character of this game is a square blue tofu called Bo. We can swipe up / down / left / right to move Bo up / down / left / right. Bo always moves in a straight line and nothing can stop it except a wall. You need to help Bo find the way out.
The picture A shows that we needs three steps to swipe Bo to the exit (swipe up, swipe left, swipe down). In a similar way, we need only two steps to make Bo disappear from the world (swipe left, swipe up)!

Look at the picture B. The exit is locked, so we have to swipe Bo to get all the keys to unlock the exit. When Bo get all the keys, the exit will unlock automatically .The exit is considered inexistent if locked. And you may notice that there are some turning signs, Bo will make a turn as soon as it meets a

turning signs. For example, if we swipe Bo up, it will go along the purple line.
Now, your task is to write a program to calculate the minimum number of moves needed for us to swipe Bo to the exit.
Input
The input contains multiple cases, no more than 40.
The first line of each test case contains two integers N and M (1≤N, M≤200), which denote the sizes of the map. The next N lines give the map’s layout, with each line containing M characters. A character is one of the following: '#': represents the wall; 'S' represents the start point of the Bo; 'E' represents the exit; '.' represents an empty block; ‘K’ represents the key, and there are no more than 7 keys in the map; 'L','U','D','R' represents the turning sign with the direction of left, up, down, right.
The first line of each test case contains two integers N and M (1≤N, M≤200), which denote the sizes of the map. The next N lines give the map’s layout, with each line containing M characters. A character is one of the following: '#': represents the wall; 'S' represents the start point of the Bo; 'E' represents the exit; '.' represents an empty block; ‘K’ represents the key, and there are no more than 7 keys in the map; 'L','U','D','R' represents the turning sign with the direction of left, up, down, right.
Output
For each test case of the input you have to calculate the minimal amount of moves which are necessary to make Bo move from the starting point to the exit. If Bo cannot reach the exit, output -1. The answer must be written on a single line.
Sample Input
5 6 ###### #....# .E...# ..S.## .##### 5 6 ###### #....# .....# SEK.## .##### 5 6 ###### #....# ....K# SEK.## .##### 5 6 ###### #....# D...E# S...L# .#####
Sample Output
3 2 7 -1
题意:给出一个迷宫,没有遇到特殊的点,就一直沿着同一方向一直往前走,一旦遇到墙了就停下,然后可以自由选择方向前进,URLD几个是强制转换方向,E是终点,如果图中有K,那么要经过所有的K获得钥匙之后,门才会开,才能离开
思路:状态压缩记录所有访问的状态
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <bitset>
#include <algorithm>
#include <climits>
using namespace std;
#define ls 2*i
#define rs 2*i+1
#define UP(i,x,y) for(i=x;i<=y;i++)
#define DOWN(i,x,y) for(i=x;i>=y;i--)
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define LL long long
#define N 205
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define rank rank1
const int mod = 10007;
struct node
{
int x,y,step,key;
};
int n,m,sx,sy,knum,kk[N][N];
char g[N][N];
bool vis[N][N][4][1<<7];
bool used[N][N][1<<7];
int to[4][2]= {1,0,0,1,-1,0,0,-1};
int check(int x,int y)
{
if(x<0||y<0||x>=n||y>=m)
return 1;
return 0;
}
int bfs()
{
int i,j;
MEM(vis,0);
MEM(used,0);
queue<node> Q;
node a,next;
a.x = sx;
a.y = sy;
a.step = 0;
a.key = 0;
Q.push(a);
used[a.x][a.y][0] = 1;
while(!Q.empty())
{
a = Q.front();
Q.pop();
for(i = 0; i<4; i++)
{
int mx=to[i][0],my=to[i][1];
int x,y,k,d;
x = a.x,y=a.y,k=a.key;
while(1)
{
if(g[x][y]=='D')
mx=1,my=0;
if(g[x][y]=='R')
mx=-0,my=1;
if(g[x][y]=='U')
mx=-1,my=0;
if(g[x][y]=='L')
mx=0,my=-1;
if(mx==1&&my==0)
d=0;
if(mx==0&&my==1)
d=1;
if(mx==-1&&my==0)
d=2;
if(mx==0&&my==-1)
d=3;
if(vis[x][y][d][k])
break;
vis[x][y][d][k] = 1;
x+=mx,y+=my;
if(check(x,y)) break;
if(g[x][y]=='#') break;
if(g[x][y]=='E'&&k==(1<<knum)-1)
return a.step+1;
if(g[x][y]=='D')
mx=1,my=0;
if(g[x][y]=='R')
mx=-0,my=1;
if(g[x][y]=='U')
mx=-1,my=0;
if(g[x][y]=='L')
mx=0,my=-1;
if(g[x][y]=='K')
k|=kk[x][y];
if(!check(x+mx,y+my)&&g[x+mx][y+my]=='#')
{
if(used[x][y][k])
break;
used[x][y][k] = 1;
next.x = x;
next.y = y;
next.key = k;
next.step=a.step+1;
Q.push(next);
break;
}
}
}
}
return -1;
}
int main()
{
int i,j;
while(~scanf("%d%d",&n,&m))
{
knum = 0;
for(i = 0; i<n; i++)
{
scanf("%s",g[i]);
for(j = 0; j<m; j++)
{
if(g[i][j]=='S')
{
sx=i,sy=j;
}
if(g[i][j]=='K')
{
kk[i][j]=1<<knum;
knum++;
}
}
}
printf("%d\n",bfs());
}
return 0;
}






















 603
603

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








