EM算法

回顾：极大似然估计

    考虑一个随机变量$X$，只能取1和2两个值中的1个，我们现在要对这个随机变量进行描述。现在已知这个随机变量服从两点分布，也就是

$$P(X=1)=\mu_1 \\ P(X=2)=\mu_2 \\ \mbox{其中} \mu_1+\mu_2=1$$
    用表格表示，就是

$$\begin{array}{c|cc} X & 1 & 2 & \\ \hline P & \mu_1 & \mu_2 \end{array}$$
    这里的 $\mu_1$和 $\mu_2$都是两点分布模型的 参数，这两个参数描述了随机变量 $X$的特性。
    我们每对$X$进行一次采样，就可以得到一个结果（1或者2），现在我们希望对 $X$进行若干次采样，通过采样结果来估计模型的参数，得到了模型的参数的估计值，也就可以知道随机变量X的特性。
    我们进行$n$次采样以后，可以得到一个计数向量 $\overrightarrow{n}=(x_1,x_2)$，其中 $x_1$和 $x_2$分别表示我们采样得到的1和2的个数， $x_1+x_2=n$。显然，这里 $\overrightarrow{n}$也是一个随机变量，它服从二项分布。
    现在我们真正地进行 $n$次采样，首先得到的是一串有顺序的类似于“11222212111”的数字，也就是我们的样本集，忽略其中的1和2的顺序，可以得到一个计数向量$\overrightarrow{n}=(n_1,n_2)$，其中 $n$、$n_1$和 $n_2$现在是已知的常数。这里显然有 $n=n_1+n_2$，则：
$$P(x_1=n_1)=C_n^{n_1}\mu_1^{n_1}(1-\mu_1)^{n-n_1}$$
    注意，上式表示的是观测结果发生的概率，但是由于参数 $\mu_1$未知，它现在是一个关于 $\mu_1$的函数（其他量都已知），这个函数叫做似然函数（这里是离散的形式）。
    极大似然估计的思路就是，找到一个 $\mu_1$，使得似然函数的值最大（也就是使得观测结果发生的概率最大），这样的 $\mu_1$就是我们的极大似然估计的结果。具体这里的做法十分简单，让似然函数对参数 $\mu_1$求导，然后令导函数为0，即可得到 $\mu_1$的估计值 $$\hat{\mu_1}={{n_1}\over{n}}$$

带隐含变量的情况

    现在考虑如下模型（例子来自《统计学习方法》）：假设有三枚硬币，分别记作$A、B和C$，这些硬币正面出现的概率分别是$\pi、p和q$。进行如下掷硬币实验：先掷硬币$A$，但是不记录结果，然后根据结果来决定是掷硬币$B$还是$C$，如果$A$是正面，则掷硬币$B$，反之掷硬币$C$，然后将这个结果记录下来，也就是说，记录下的都是掷硬币$B$或者$C$的结果。独立地重复$n$次实验（这里$n=10$），观测结果如下：

$$1,1,0,1,0,0,1,0,1,1$$
    假设只能观测到掷硬币的结果，现在我们来估计三硬币正面出现的概率，也就是三硬币模型的所有三个参数。
    我们用 $y$表示观测变量，它只能取0或者1；用$z$表示隐含变量，它表示掷硬币 $A$的结果；$\theta=(\pi,p,q)$是模型的参数。注意， $y$可以观测，而$z$不可观测。
    三硬币模型中 $y$的分布可以写作
$$\begin{align} P(y\mid\theta) &=\sum_zP(y,z\mid\theta)=\sum_zP(z\mid\theta)P(y\mid z,\theta) \\ &=\pi p^y(1-p)^{1-y}+(1-\pi)q^y(1-q)^{1-y} \end{align}$$
    将观测数据表示为 $Y=(Y_1,Y_2,\cdots ,Y_n)^T$，隐含的变量的取值表示为 $Z=(Z_1,Z_2,\cdots ,Z_n)^T$，则观测数据的似然函数为
$$P(Y\mid\theta)=\sum_zP(Z\mid\theta)P(Y\mid Z,\theta)$$
    即
$$P(Y\mid\theta)=\prod_{j=1}^n{[\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi)q^{y_j}(1-q)^{1-y_j}]}$$
    考虑求模型参数 $\theta=(\pi,p,q)$的极大似然估计，即
$$\hat{\theta}=\mathop{argmax}_\theta logP(Y\mid\theta)$$
    由于对数函数里面有求和符号，这时候让似然函数对参数求偏导然后令偏导数为零是不可行的，这时候就需要用EM算法了。
    下面直接给出针对以上问题的EM算法。EM算法首先选取参数的初值（有时候会随机选初值），我们把初值记作 $\theta^{(0)}=(\pi^{(0)},p^{(0)},q^{(0)})$，然后通过下面的步骤迭代计算参数的估计值，直到收敛到局部最优解，这个局部最优解使得似然函数的值极大。第 $i$次迭代参数的估计值为$\theta^{(i)}=(\pi^{(i)},p^{(i)},q^{(i)})$。EM算法的第 $i+1$次迭代如下。
     E步：计算在模型参数 $\theta^{(i)}$下观测数据 $y_j$来自硬币B的概率
$$\mu_j^{(i+1)}={{\pi^{(i)}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j}} \over {\pi^{(i)}(p^{(i)})^{y_j}(1-p^{(i)})^{1-y_j}+(1-\pi^{(i)})(q^{(i)})^{y_j}(1-q^{(i)})^{1-y_j}}}$$
     M步：计算模型参数的新估计值
$$\pi^{(i+1)}={1 \over n}\sum^n_{j=1}\mu_j^{(i+1)} \\ p^{(i+1)}={ {\sum^n_{j=1}\mu_j^{(i+1)}y_j} \over {\sum^n_{j=1}\mu_j^{(i+1)}} } \\ q^{(i+1)}={ {\sum^n_{j=1}(1-\mu_j^{(i+1)})y_j} \over {\sum^n_{j=1}(1-\mu_j^{(i+1)})} }$$
    不断重复E步和M步，就可以得到参数的一组局部最优解。其实上面的E步和M步都是很好理解的，在E步的时候，我们已知模型的参数以及观测值，求隐含变量的分布变得很容易；而在M步的时候，我们已知模型的隐含变量的分布，于是这时候问题变成了普通的极大似然估计问题（即相当于没有隐含变量），于是求出一组新的参数也十分容易。
    因此，现在我们对于EM算法可以有一个感性的理解：由于隐含变量的存在，我们没有办法直接对似然函数最大化。但是如果知道了隐含变量的分布，我们可以很方便地对参数进行估计；如果知道了参数的值，我们可以很方便地求出隐含变量的分布。于是就可以不断迭代求出参数的局部最优值，只是最开始的时候，参数需要一个初始值。

从一个维度理解EM算法的原理

    现在我从一个维度说说EM算法的原理（公式来自PRML这本书）。首先，约定一些符号的意义。$X$表示观测变量，$Z$表示隐含变量，$\theta$表示模型参数的集合。
    我们的目标是求$\theta$的极大似然估计值，即

$$\hat{\theta}=\mathop{argmax}_\theta \ln p(X\mid\theta)$$
    而 $\ln p(X\mid\theta)=\ln \sum_Z p(X,Z\mid\theta)$，由于对数里面带有求和符号，无法直接对似然函数极大化，因此要考虑曲线救国。
    如果定义隐含变量的分布为 $q(Z)$，则
$$\begin{align} \ln p(X\mid\theta)&=\sum_Z q(Z)\ln p(X\mid\theta) \\ &=\sum_Z q(Z)\ln{ {p(X,Z\mid\theta)} \over {p(Z\mid X,\theta)} } \\ &=\sum_Z q(Z)\ln{ {{p(X,Z\mid\theta)}\over{q(Z)}} \over {{p(Z\mid X,\theta)}\over{q(Z)}} } \\ &=\sum_Z q(Z)\ln{{p(X,Z\mid\theta)}\over{q(Z)}}-\sum_Z q(Z)\ln{{p(Z\mid X,\theta)}\over{q(Z)}}\tag{1} \end{align}$$
    我们记
$$\begin{eqnarray} \mathcal{L}(q,\theta)&=&\sum_Z q(Z)\ln{{p(X,Z\mid\theta)}\over{q(Z)}}\tag{2} \\ KL(q\mid\mid p)&=&-\sum_Z q(Z)\ln{{p(Z\mid X,\theta)}\over{q(Z)}}\tag{3} \end{eqnarray}$$
    其中 $\mathcal{L}(q,\theta)$是 $q(Z)$的泛函形式， $KL(q\mid\mid p)$是 $q(Z)$和 $p(Z\mid X,\theta)$的 $KL$散度， $KL$散度在这里就不做具体介绍了，它是一个衡量两个分布相似程度的函数，两个分布越相似，它就越趋向于0，但是它始终大于等于0，当且仅当两个分布完全相同时，它等于0。
    观察 $(1)$可知，想找一组 $\theta$使得左边最大，我们可以找一组 $\theta$使得右边最大，即使得 $(2)$和 $(3)$的和最大。
    这时候，考虑如果 $\theta$已知会发生什么。如果 $\theta=\theta^{(i)}$已知，则 ${p(X,Z\mid\theta^{(i)})}$和 ${p(Z\mid X,\theta^{(i)})}$都已知，则 $(2)$和 $(3)$完全由 $q(Z)$决定。现在我们选择 $q(Z)=p(Z\mid X,\theta^{(i)})$，于是
$$\begin{align} KL(q\mid\mid p)&=0 \\ \ln p(X\mid\theta^{(i)})&=\mathcal{L}(q,\theta^{(i)}) = \sum_Z q(Z)\ln{{p(X,Z\mid\theta^{(i)})}\over{q(Z)}}\tag{4} \end{align}$$
    注意，此时的 $\theta=\theta^{(i)}$，而且 $q(Z)={p(Z\mid X,\theta^{(i)})}$，于是 $(4)$的两边其实都是确定的值。这时候，如果我们变动 $(4)$中 ${p(X,Z\mid\theta^{(i)})}$的 $\theta$，则 $(4)$的两边会随着变动，这时候我们找到 $\theta=\theta^{(i+1)}$，使得 $(4)$右边极大，即 $(4)$的右边现在其实等于
$$\sum_Z q(Z)\ln{{p(X,Z\mid\theta^{(i+1)})}\over{q(Z)}}=\sum_Z p(Z\mid X,\theta^{(i)})\ln{{p(X,Z\mid\theta^{(i+1)})}\over{{p(Z\mid X,\theta^{(i)})}}}$$
    但是 $\theta$一变动， $(3)$中的 $p(Z\mid X,\theta)$就会变动，此时 $p(Z\mid X,\theta^{(i+1)})$和 $q(Z)=p(Z\mid X,\theta^{(i)})$不再相等，于是 $KL(q\mid\mid p)$不再为0， $(4)$不再成立，我们需要找到一个新的 $q(Z)={p(X,Z\mid\theta^{(i+1)})}$。
    总体来说，流程大概就是这样：确定 $\theta$以后，找合适的 $q(Z)$使得 $(3)$为0，然后更新 $\theta$使得 $(1)$的右边极大化，但是 $(1)$的右边极大化的同时， $(1)$的左边比它增长得更快，因为此时 $(3)$不再为0了，于是我们要基于当前的 $\theta$重新找一组合适的 $q(Z)$。
    下面来说明如何由当前的 $q(Z)$更新 $\theta$的值：
$$\begin{align} \mathcal{L}(q,\theta)&=\sum_Z q(Z)\ln{{p(X,Z\mid\theta)}\over{q(Z)}} \\ &=\sum_Z {p(Z\mid X,\theta^{(i)})}\ln{{p(X,Z\mid\theta)}\over{{p(Z\mid X,\theta^{(i)})}}} \\ &= \sum_Z {p(Z\mid X,\theta^{(i)})}\ln p(X,Z\mid\theta) - \sum_Z {p(Z\mid X,\theta^{(i)})}\ln p(Z\mid X,\theta^{(i)}) \\ &= \sum_Z {p(Z\mid X,\theta^{(i)})}\ln p(X,Z\mid\theta) - const \tag{5} \end{align}$$
     $(5)$右边的第一项就是 $Z$对于全数据分布的期望，也就是$E_Z[\ln p(X,Z\mid\theta)]$，由于此时隐含变量 $Z$的分布是已知的，相当于模型中全都是观测变量，于是极大化$E_Z[\ln p(X,Z\mid\theta)]$是非常容易的，于是我们可以轻松找到
$$\theta^{(i+1)}=\mathop{argmax}_{\theta} E_Z[\ln p(X,Z\mid\theta)]$$
    所以，EM算法的E和M两步的名称就很好理解了，E步就是由 $\theta^{(i)}$求隐含变量 $Z$的分布，由$Z$的分布求出全数据的数学期望（Expectation），M步就是极大化（Maximization）这个期望，得到一组新的参数 $\theta^{(i+1)}$，如此迭代直到收敛，就是EM算法。
    下面这张图来自PRML这本书，它形象展示了EM算法：

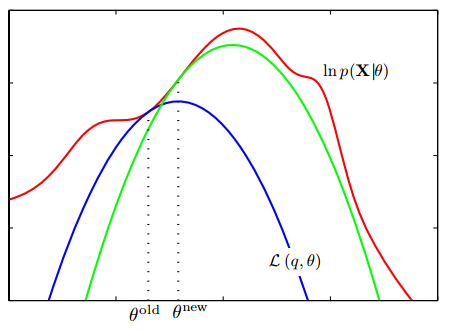
    图中红色的函数就是原似然函数 $\ln p(X\mid\theta)$，而蓝色的函数就是 $\mathcal{L}(q,\theta)$，我们对 $\mathcal{L}(q,\theta)$极大化了以后（即找到一组 $\theta^{new}$），原似然函数 $\ln p(X\mid\theta)$比它增长更快，于是我们不得不再找一个新的 $\mathcal{L}(q,\theta)$，对新的函数极大化，最后直到收敛到 $\ln p(X\mid\theta)$的局部极大值。