CS229 Lecture 6

CS229 Lecture 6

---

本节课重点

Naive Bayes
神经网络
支持向量机

---

回顾上节课的内容：

将一封邮件表示成一个向量$\left[\begin{array}{c}1\\ 0\\ ⋮\\ 1\\ ⋮\end{array}\right]$，这个向量的长度为字典的大小,这个向量中的数字只能为0和1,即存在或者不存在。将其表示为生成学习算法的模型为：
$$\begin{gathered} p(x|y)=\prod _{i=1}^{n}p(x_i|y) \\ arg\underset{y}{\max }p(y|x)=arg\underset{y}{\max }p(x|y)p(y) \end{gathered}$$
这个模型一般被称为多元伯努利事件模型。

---

变种1：

上面的模型中由邮件表示的向量，其元素只能为0或者1，现在改为 x i ∈ { 0 , 1 , ⋯   , k } x_i\in\{0,1,\cdots,k\} xi​∈{0,1,⋯,k}。那么生成学习模型的$p(x|y)={\prod }_{i=1}^{n}p(x_i|y)$。这时的$x_i$属于多项式分布而非原来的伯努利分布。

如果由一个变量属于连续变量如何将其离散化为$k$个值。比如将房屋居住面积离散为几个值那么：

$livingarea$	$<500$	$500\sim 1000$	$1000\sim 1500$	$\cdots$
x	1	2	3	-

---

变体2：多项式事件模型

因为前面的模型都忽略了每个词出现的次数，词出现的次数可能对于文本的分类，如是否为一封垃圾邮件有很大的影响。现在对于一封邮件将其表示为 { x 1 ( i ) , x 2 ( i ) , x 3 ( i ) , x 4 ( i ) , ⋯ x n i ( i ) } \{x_{1}^{(i)},x_{2}^{(i)},x_{3}^{(i)},x_{4}^{(i)},\cdots x_{n_{i}}^{(i)} \} {x1(i)​,x2(i)​,x3(i)​,x4(i)​,⋯xni​(i)​}，其中$n_i$表示第$i$封邮件的单词数目。且 x j ∈ { 1 , 2 , 3 , ⋯ 50000 } x_j\in\{1,2,3,\cdots 50000\} xj​∈{1,2,3,⋯50000}。这个模型的对应生成学习算法为：

$p(xy)=({\prod }_{i=1}^{n}p(x_i|y))p(y)$

模型涉及到的参数为：
${\varphi }_{k|y=1}=p(x_j=k|y=1)$
${\varphi }_{k|y=0}=p(x_j=k|y=0)$
${\varphi }_y=p(y=1)$

关于这些参数的极大似然估计为：
ϕ k ∣ y = 1 = ∑ i = 1 m 1 { y i = 1 } ∑ j = 1 n i 1 { x j i = k } ∑ i = 1 m 1 { y ( i ) = 1 } n i \phi_{k|y=1}=\frac{\sum_{i=1}^{m}1\{y^{i}=1\}\sum_{j=1}^{n_{i}}1\{x_{j}^{i}=k\}}{\sum_{i=1}^{m}1\{y^{(i)}=1\}n_{i}} ϕk∣y=1​=∑i=1m​1{y(i)=1}ni​∑i=1m​1{yi=1}∑j=1ni​​1{xji​=k}​

如果对上式子添加Laplace 平滑处理则有：

ϕ k ∣ y = 1 = ∑ i = 1 m 1 { y i = 1 } ∑ j = 1 n i 1 { x j i = k } + 1 ∑ i = 1 m 1 { y ( i ) = 1 } n i + 50000 \phi_{k|y=1}=\frac{\sum_{i=1}^{m}1\{y^{i}=1\}\sum_{j=1}^{n_{i}}1\{x_{j}^{i}=k\}+1}{\sum_{i=1}^{m}1\{y^{(i)}=1\}n_{i}+50000} ϕk∣y=1​=∑i=1m​1{y(i)=1}ni​+50000∑i=1m​1{yi=1}∑j=1ni​​1{xji​=k}+1​

其中假设字典的大小为$50000$

关于Laplace 平滑分母添加的值：

如果说 x i ∈ { 1 , 2 , 3 , ⋯   , l } x_i\in\{1,2,3,\cdots,l\} xi​∈{1,2,3,⋯,l},那么$p(x=k)=\frac{观测到x=k的数目+1}{观测到的x数目+l}$。

求解极大似然估计的公式为：

$L({\varphi }_{k|y=1},{\varphi }_{k|y=0},{\varphi }_y)=log{\prod }_{i=1}^{m}p(x^{(i)},y^{(i)};{\varphi }_{k|y=1},{\varphi }_{k|y=0},{\varphi }_y)=log{\prod }_{i=1}^m{\prod }_{j=1}^{n_i}p(x_j^{(i)}|y^{(i)};{\varphi }_{k|y=1},{\varphi }_{k|y=0})p(y^{(i)};{\varphi }_y)$

---

非线性分类器

前面学到的逻辑回归只是线性分类器，但是在有些情况下数据并非线性可分的。这时就需要用到非线性分类器。

---

神经网络

神经网络分为输入层，隐层和输出层。通过反向传播(梯度下降)求解最优参数。

$$J(\theta )=\frac{1}{2}\sum _{i=1}^m(y^{(i)}-h_{\theta }(x^{(i)}){)}^2$$

---

SVM

支持向量机算法是一种高效无需定制可以作为线性分类的算法，并且对其进行部分优化后，可以转化为非线性分类算法。

在前面学习的逻辑回归中：

如果${\theta }^{T}x\ge 0$,那么算法认为预测值为1

如果${\theta }^{T}x<0$,那么算法认为预测值为0.

如果说${\theta }^{T}x\gg 0$,那么我们很确信预测值就是1.

如果说${\theta }^{T}x\ll 0$,那么我们很确信预测值就是0。

我们训练一个分类算法，我们认为这个算法训练的好，不仅要求其对数据分类正确，而且要求其对分类结果十分确信。即：

$\forall is.t{y}^{(i)}=1have{\theta }^{T}x\gg 0$
$\forall is.t{y}^{(i)}=0have{\theta }^{T}x\ll 0$

---

下面假设数据线性可分。

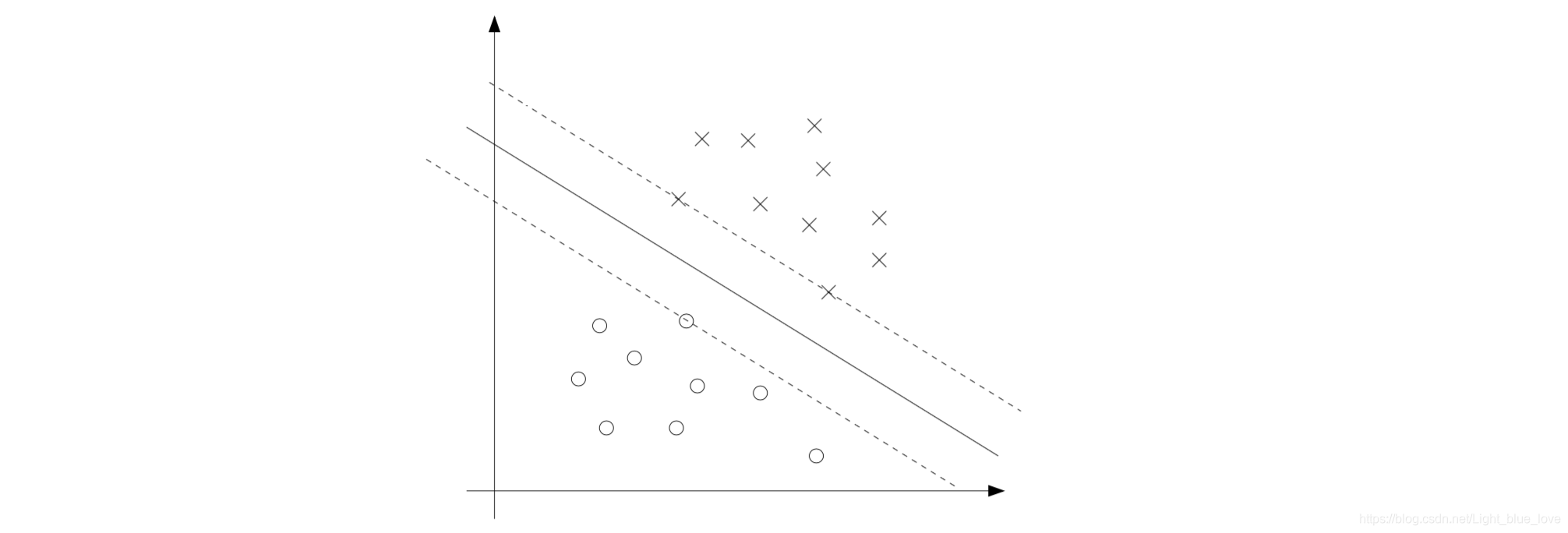
从上面的图片中可以看出有三条线均可以将数据圆和叉分开，但是哪一条线才是最好的呢，很明显当然是中间的那条实线。因为这条线对两类数据都有一定的间隔，而两条虚线均对某类数据太过靠近，以至于只要边界上某个点稍微移动一点点，那么就可能会预测错误。

符号定义

在SVM中 y ∈ { − 1 , 1 } y\in\{-1,1\} y∈{−1,1},因此 h ∈ { − 1 , 1 } h\in\{-1,1\} h∈{−1,1}。且在现在的设定中去掉了$x_0=1$这一项$h_{w,b}(x)=g(w^{T}x+b)$。现在公式中的$w$相当于$\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ ⋮\\ {\theta }_n\end{array}\right]$，而$b$相当于${\theta }_0$。其中$g(z)=\{\begin{array}{ll}1& ifz\ge 0\\ -1& otherwise\end{array}$。$w$是$n$维向量。

函数间隔(Function Margin of hyper plane w,b)

对于一个分类样本$(x^{(i)},y^{(i)})$其对于分类超平面($w,b$)的函数间隔的定义为${\hat{\gamma }}^{(i)}=y^{(i)}(w^T{x}^{(i)}+b)$。

如果$y^{(i)}=1$,我们期望$w^T{x}^{(i)}+b\gg 0$

如果$y^{(i)}=-1$,我们期望$w^T{x}^{(i)}+b\ll 0$

$y^{(i)}(w^T{x}^{(i)}+b)>0$,这样分类才是正确的。

对于整个训练集的函数间隔的定义为$\hat{\gamma }=\underset{i}{\min }{\hat{\gamma }}^{(i)}$,在前面说过，仅仅正确预测是不够的，还需要使得预测结果可信度很大，即需要使得$\hat{\gamma }$尽可能大，通过观察函数间隔的定义我们可以很容易的想到$w\to 2wb\to 2b$就可以使$\hat{\gamma }翻倍$。但是也很容易理解这样单纯的是$\hat{\gamma }$最大并没有什么意义，我们需要限制$||w||=1$，然后最大化$\hat{\gamma }$才有意义。

几何间隔

上面讨论了函数间隔，现在看看几何间隔。上图中点$A$到分解线的距离为$\gamma$,交点为$B$,因为$B$在分隔线上因此满足$w^T(x^{(i)}-{\gamma }^{(i)}\frac{w}{||w||})+b=0$，其中点$A$的坐标为$x^{(i)}$,点$B$的坐标被表示为$x^{(i)}-{\gamma }^{(i)}\frac{w}{||w||}$。进而可以得出：
$$\begin{gathered} w^T{x}^{(i)}+b={\gamma }^{(i)}\frac{w^{T}w}{||w||}={\gamma }^{(i)}||w|| \\ {\gamma }^{(i)}=\frac{w^T}{||w||}x+\frac{b}{||b||} \end{gathered}$$

通常我们会将几何间隔表示为：
$${\gamma }^{(i)}=y^{(i)}[\frac{w^T}{||w||}{x}^{(i)}+\frac{b}{||b||}]$$

可以看出如果说$||w||=1$,那么${\hat{\gamma }}^{(i)}={\gamma }^{(i)}$,但是更一般的情形是${\gamma }^{(i)}=\frac{{\hat{\gamma }}^{(i)}}{||w||}$。

对于一批数据其几何间隔的定义为：

$$\gamma =\underset{i}{\min }{\gamma }^{(i)}$$

---

最大间隔分类器

其主要思想就是让间隔最大，进而使得预测出来的结果更为可信。

$$\begin{gathered} \underset{\gamma ;w,b}{\max }\gamma \\ s.t{y}^{(i)}(w^T{x}^{(i)}+b)\ge \gamma \\ ||w||=1 \end{gathered}$$

在这些限定下即使让$w\to 10w,b\to 10b$也不会改变其几何间隔。

---

函数间隔的定义应当是来源于直观理解：逻辑回归中，只要${\theta }^{T}x>0$,那么我们就认为其预测结果为1，我们知道${\theta }^{T}x$的值越大，那么其预测出来的结果越可信，因为计算出来的值刚好距离分界线不远，你说它是正常邮件还是垃圾邮件都是可以的，如果说${\theta }^{T}x\gg 0$，那么我们认为它有很大几率是一封垃圾邮件。在支持向量机中$g(z)=\{\begin{array}{ll}1& ifz\ge 0\\ -1& otherwise\end{array}$,其中$z=w^{T}x+b$,因此有了函数间隔的定义${\hat{\gamma }}^{(i)}=y^{(i)}(w^T{x}^{(i)}+b)$,即这个值越大约可信，但是如果没有限定条件单纯的大没有什么用，因此引入了几何间隔，几何间隔是来自于对几何距离的直观求解。