数学-三角函数及其图像

目录：

一、基本定义

二、同角三角函数基本关系

三、特殊值

四、诱导公式

五、基本公式

六、和差角公式

七、倍角公式与半角公式

1、通过和差角公式推导

2、通过欧拉公式推导

八、积化和差与和差化积

九、万能公式

十、有趣的函数图像

1、r = cosθ

2、r² = cosθ

3、r = sin(θ/3)

4、f(x,y) = sinx-x²y²-1 = 0

---

一、基本定义

设角α的终边与单位圆交于点 P(x,y)，则有：

二、同角三角函数基本关系

由上边的式子可以直接得出以下三个关系式(倒数关系)：

还可以得出如下商的关系：

结合勾股定理，我们还可以得到下述平方关系：

这些关系式很简单，就不推导了。

三、特殊值

当这篇文章读完之后，你一定可以推导出下表中任何一个值。

角度与弧度： Intuitive Guide to Angles, Degrees and Radians

三角函数使用弧度表示

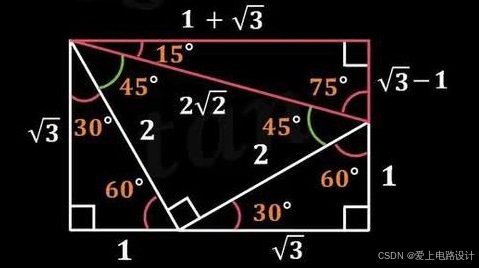
四、诱导公式

我不推荐大家记这个表，而是希望大家先熟悉一下最基本的三个三角函数 (sin、cos和tan) 的性质，然后再讨论遇到类似问题如何最快速地推导。

①正弦函数是奇函数，最小正周期为 2π，其导函数为余弦函数；

②余弦函数是偶函数，最小正周期为 2π，其导函数为正弦函数的相反数；

③正切函数是奇函数，最小正周期为 π。

诱导公式的目的是什么呢？就是将 sin(kπ/2+α) 中 π/2 的整数倍去掉，仅保留 α。因此我们可以按照上述性质一步步地化简：

①按照其奇偶性，将 α 变为负值；

②根据正弦/余弦函数的周期性，将 2π 的整数倍全部去掉。若此时被加数为负，则再加上 2π；

③若被加的数绝对值仍不小于 π，就将其绝对值直接减去 π，然后取负号；

④利用公式得到结果。

可以看出，按照这个步骤，完全不需要记忆那么多公式，甚至连「奇变偶不变，负号看象限」都不需要，只要按部就班地做就可以得到正确答案。而正切函数更简单，因为其最小正周期是 π，因此最后只有加不加 π/2 的问题。

五、基本公式

下面看一个最基本的公式，这个公式很自然，但是确实下边各个公式推导的基础。

平面上两个单位向量，与 x 轴正向夹角分别为 x 和 y，则这两个向量分别为 (cosx,sinx)、(cosy,siny)。则这两个向量的点积为 cosx*cosy+sinx*siny，而点积又可以表示为 1*1*cos(x-y) = cos(x-y)，向量的点乘与叉乘。于是我们得到了以下公式：

这就是最基本的公式。从向量的角度，这个公式也是很自然的。

六、和差角公式

将(1)中的 y 用 -y 代入，即可得到

将(1)中的 x 用 π/2-x 代，再利用诱导公式，可以得到正弦函数的和差角公式：

(3)式的 y 代成 -y，有

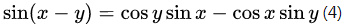
(3)/(2)、(4)/(1)得到正切函数的和差角公式：

七、倍角公式与半角公式

1、通过和差角公式推导

有了“六、和差角公式”中的式子，令 x = y，很容易得到倍角公式和半角公式：

注意到(8)式，由平方关系 sin²x + cos²x = 1又可以写成 cos(2x) = 2cos²x-1 或 cos(2x) = 1-2sin²x。

所以就有半角公式(也叫降幂公式)：

两式相除，得

2、通过欧拉公式推导

我们也可以从“欧拉公式”(数学的精美之4、欧拉公式推导★)推导，在电子行业中，i 通常用来表示电流，故虚数单位用 j 来表示。

推导结果如下图：

原文件：欧拉公式推导

这就是上面的倍角公式(7)和(8)。更一般地表示：

这就是传说中的“棣莫弗定理”。

八、积化和差与和差化积

回头看看(3)式和(4)式，两式相加得到。

而相减则得

(1)+(2)、(1)-(2)同样可以得到两个积化和差的公式：

然后在上式中，令 u = x+y、v = x-y。此时 x = (u+v)/2，y = (u-v)/2，立刻就得到了四个和差化积公式：

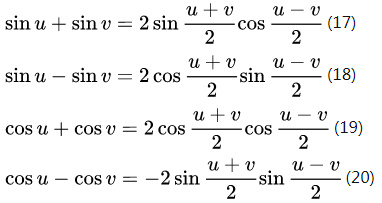
九、万能公式

万能公式是将 sinx、cosx 和 tanx 均用 tan(x/2) 表示。由于后者的值域为整个实数区间，因此方便考察许多性质。

首先我们知道，tanx 的万能公式就是其二倍角公式(9)式。我们试着推导一下余弦函数的万能公式。

正弦的就简单了，两个一乘就行：

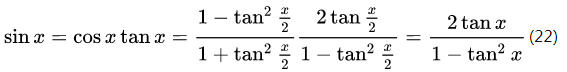
十、有趣的函数图像

1、r = cosθ

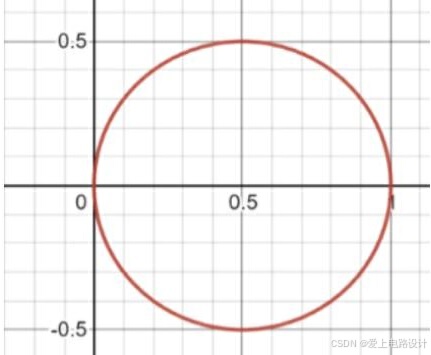
2、r² = cosθ

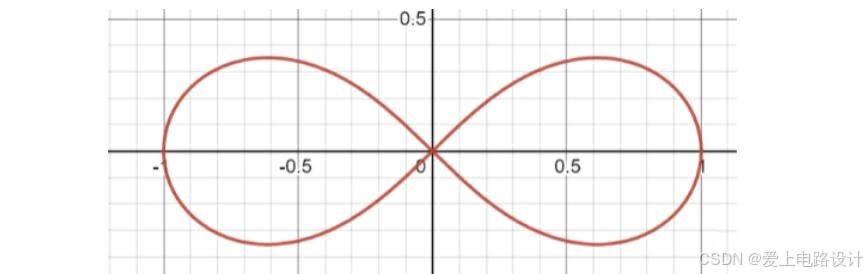
3、r = sin(θ/3)

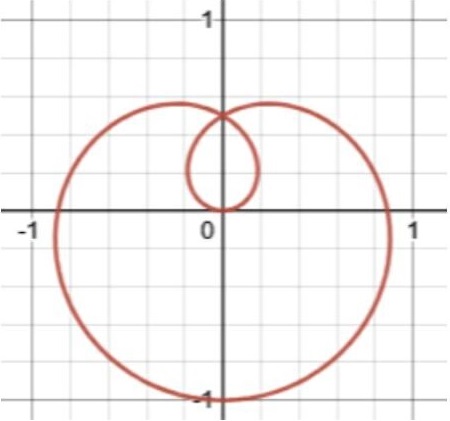
4、f(x,y) = sinx-x²y²-1 = 0

---

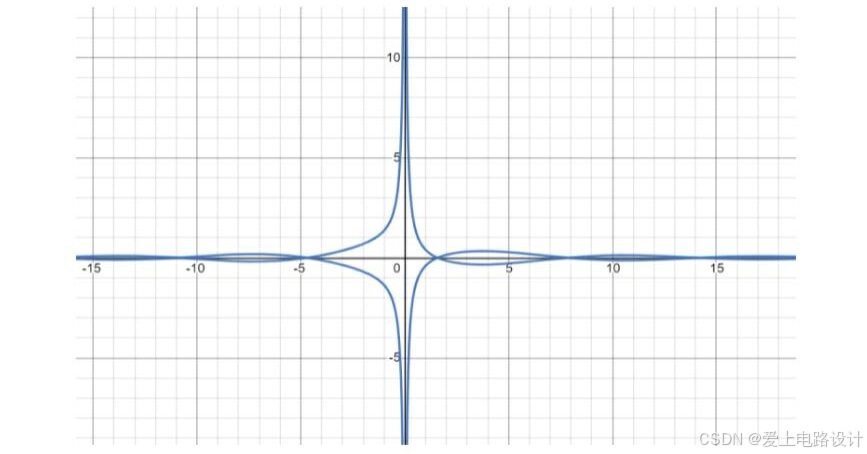
君子生非异也，善假于物也。 觉得不错，动动发财的小手点个赞哦！