P02114058郭梓阳——相对熵的非负性的推导

目录

一、Jensen不等式证明

二、相对熵

1、相对熵的定义

2、非负性证明

 

 

    首先我们简要介绍一下熵的概念。“熵”这一概念并不仅仅存在于物理化学中，还应用于信息论中。熵是结果不确定度的一种度量。shannon熵定义为：

其中X为随机变量，它在K个事件x1,x2,x3离散集合上的概率有P(xi)
 ps:我们可以试着证明一下当其实均匀分布时，它的熵值最大。

相对熵又称KL散度，信息散度，是两个概率分布间差异的非对称性度量。令P(X),Q(X)是随机变量X的概率分布，则在其实离散型随机变量的情况下，相对熵为：

  故我们观察相对熵的形式可以发现，它可以看做是对数几率(计分矩阵中的分值)的期望，即将P(X)看做是在匹配模型M中的残基a,b的联配概率，而Q(X)看做是无关模型中的残基a,b的独立出现的概率。故相对熵可作为模型的期望分值。
  回归本文的主题，即证明相对熵的正定性。因为证明的过程中用到了jensen
不等式，所以我们先证明一下jensen不等式。

一、Jensen不等式证明

以下凸函数为例

 

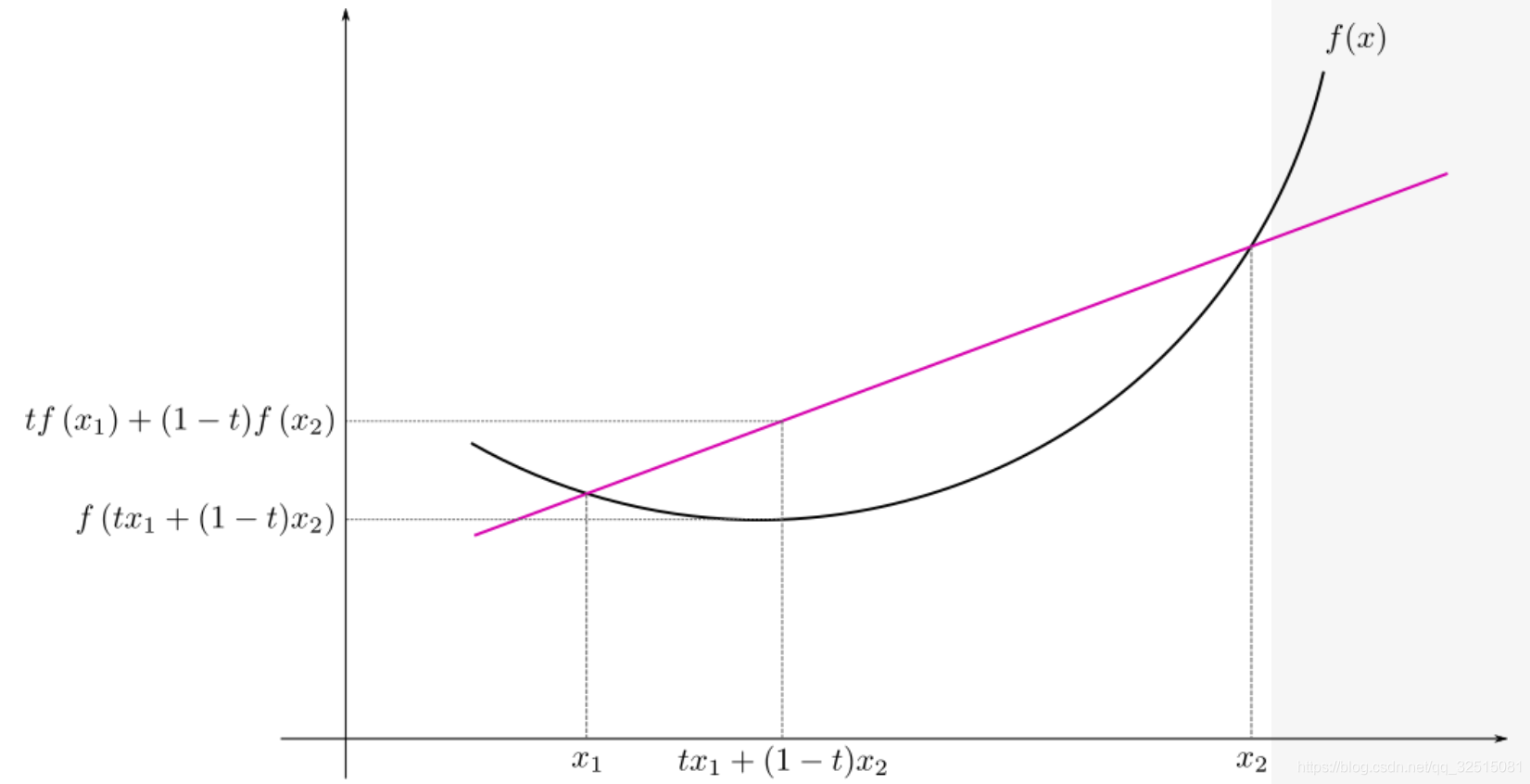
Jensen不等式概括了凸函数的割线位于函数图上方的陈述，这是Jensen对两点的不等式：割线由凸函数的加权均值组成（对于 t∈[0,1]）：

函数的图形是加权均值的凸函数:

因此，Jensen 不等式是 :

推广到n个点，即

其中

当且仅当 x1=x2=...=xn时成立。

二、相对熵

1、相对熵的定义

关于相对熵的理解CSDN上已经有大量文献可研究，本文侧重于对相对熵非负性的研究。在此只简单阐述。
相对熵 (Relative Entropy) 也称 KL 距离，设   是离散随机变量  的两个概率分布，则 p(x)对 q(x) 的相对熵是:

其中

2、非负性证明

由于

令,则

再令f(x)=xlogx,易得f(x)=xlogx为下凸函数

则

即

当且仅当x1=x2=x3=...=xn,即

即当且仅当时成立,证明完毕。

由于相对熵是非负的，通常可用该性质证明信息论中的一些定理和性质。