迷宫问题【菜鸟学习日记】

今天学习一个关于栈的经典问题—迷宫问题！

这个问题我们分别用栈和递归两种方法分别来实现一下

还有就是我们分别考虑几种情况去实现和改进优化

1、如果有多条通路
2、找最短路径
3、带环的路径

---

关于问题没有什么可多描述的，就是迷宫，找通路
写迷宫，当然要先有迷宫呀！
先写个迷宫地图

template<size_t N>
class Maze//maze（迷宫）
{
public:
    //1、二维数组传参
    //方法一：
    /*Maze(int maze[][N])
    {
        for (int i = 0; i < N; i++)
        {
            for (int j = 0; j < N; j++)
            {
                _maze[i][j] = maze[i][j];
            }
        }
    }*/

    //方法二：
    Maze(int* maze)
    {
        for (int i = 0; i < N; i++)
        {
            for (int j = 0; j < N; j++)
            {
                _maze[i][j] = maze[i*N + j];
            }
        }
    }
    ...
protected:
    int _maze[N][N];
};

void test()
{
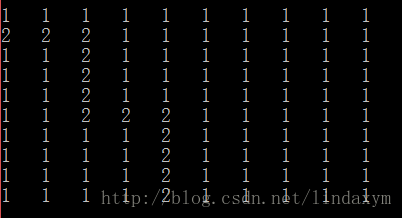
   int maze[10][10] =
    {
        { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
        { 0, 0, 0, 1, 1, 1, 1, 1, 1, 1 },
        { 1, 1, 0, 1, 1, 1, 1, 1, 1, 1 },
        { 1, 1, 0, 1, 1, 1, 1, 1, 1, 1 },
        { 1, 1, 0, 1, 1, 1, 1, 1, 1, 1 },
        { 1, 1, 0, 0, 0, 1, 1, 1, 1, 1 },
        { 1, 1, 1, 1, 0, 1, 1, 1, 1, 1 },
        { 1, 1, 1, 1, 0, 1, 1, 1, 1, 1 },
        { 1, 1, 1, 1, 0, 1, 1, 1, 1, 1 },
        { 1, 1, 1, 1, 0, 1, 1, 1, 1, 1 },
    };

   Maze<10> mz((int*)maze);//将数组传过去
    ...
}

打印出来看看

好了，地图出来了，就要开始走了，找通路
0为路，1为墙
入口点为（1，0）
这里我们每个点是一个二维坐标，有行和列，所以设置一个结构体变量来放坐标点

struct Pos
{
    int _row;//行
    int _col;//列
}

那我们来考虑一下通路的条件吧
首先我们要检查一下我们下一个走的点，
1、为0，是通路
2、不能超出边界

    bool CheckAccess(Pos pos)//边界检查+点是否合格
    {
        if (pos._row<N&&pos._row>=0
            &&pos._col<N&&pos._col>=0
            &&_maze[pos._row][pos._col] == 0)
        {
            return true;
        }
        return false;
    }

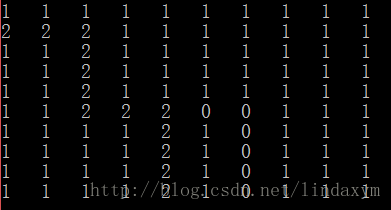
接下来该走了，走过的路，标为2

        bool GetPath(Pos entry)
    {
        Pos cur = entry;

        while (true)
        {
            _maze[cur._row][cur._col] = 2;
            //检查是否已到出口
            if (cur._row == N - 1)
            {
                return true;
            }

            //没有到出口，合法的点
            //探测（上下左右）
            Pos next = cur;
            //上
            next._row -= 1;
            if (CheckAccess(next))
            {
                cur = next;
                continue;
            }
            //下
            next = cur;
            next._row += 1;
            if (CheckAccess(next))
            {
                cur = next;
                continue;
            }
            //左
            next = cur;
            next._col -= 1;
            if (CheckAccess(next))
            {
                cur = next;
                continue;
            }
            //右
            next = cur;
            next._col += 1;
            if (CheckAccess(next))
            {
                cur = next;
                continue;
            }

           return false;
        }
    }

这是最简单的一种，但当迷宫如果有两条通路时，就不行了，而且也无法记录我们走过的路径

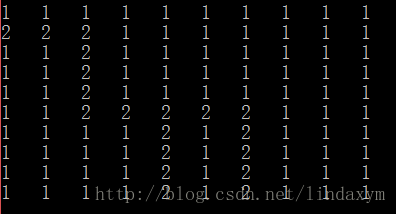
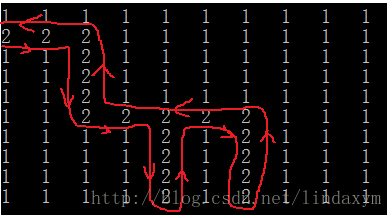
所以要进行改进，我们用栈来解决这个问题
首先我们先把入口点压入栈中，然后我们去探测周围的点，某一个有通路就走，没有通路，就出栈，返回上一个点，探测其它方向，一直这样循环，知道出栈空，退回到入口处，把所有通路就都走了一遍

    void GetPath(Pos entry, stack<Pos>& path)
    {
        path.push(entry);

        while (!path.empty())
        {
            Pos cur = path.top();
            _maze[cur._row][cur._col] = 2;

            //上
            Pos next = cur;
            next._row -= 1;
            if (CheckAccess(next))//判是否合格
            {
                cur = next;
                path.push(cur);//合格就入栈
                continue;
            }
            //下
            next = cur;
            next._row += 1;
            if (CheckAccess(next))
            {
                cur = next;
                path.push(cur);
                continue;
            }
            //左
            next = cur;
            next._col -= 1;
            if (CheckAccess(next))
            {
                cur = next;
                path.push(cur);
                continue;
            }
            //右
            next = cur;
            next._col += 1;
            if (CheckAccess(next))
            {
                cur = next;
                path.push(cur);
                continue;
            }

            //回溯
           path.pop();
        }
    }

---

来面我用递归实现

递归实现

递归实现有一个特点，就是递归本身的特性，可以实现天然的回溯，栈是Pop点回溯，而递归本身就可以回溯，当探测周围没有通路，就返回上一级调用，天然回溯到上一个点

   //递归写法（天然回溯）
    bool GetPath(Pos entry, stack<Pos>& path)
    {
        path.push(entry);

        while (!path.empty())
        {
            Pos cur = path.top();
            _maze[cur._row][cur._col] = 2;


            Pos next = cur;
            //上
            next._row -= 1;
            if (CheckAccess(next))//判是否合格
            {
                if (GetPath(next, path))
                {
                    return true;
                }
            }
            //下
            next = cur;
            next._row += 1;
            if (CheckAccess(next))
            {
                if (GetPath(next, path))
                {
                    return true;
                }

            }
            //左
            next = cur;
            next._col -= 1;
            if (CheckAccess(next))
            {
                if (GetPath(next, path))
                {
                    return true;
                }

            }
            //右
            next = cur;
            next._col += 1;
            if (CheckAccess(next))
            {
                if (GetPath(next, path))
                {
                    return true;
                }
            }
            //回溯
            return false;//返回上一层调用，天然回溯
        }
    }

结果和上面一样，走的过程也一样，只是回溯的原理不太一样而已

---

带环迷宫

bool GetPathR(Pos entry, stack<Pos>& path)//(path 路径）//用库里的栈
    {
        path.push(entry);

        while (!path.empty())
        {
            Pos cur = path.top();

            //检查是否已到出口

            //没有到出口，合法的点
            //探测（上下左右）
            Pos next = cur;
            //上
            next._row -= 1;
            if (CheckAccess(cur, next))//判是否合格
            {
                _maze[next._row][next._col] = _maze[cur._row][cur._col] + 1;
                if (GetPathR(next, path))
                {
                    return true;
                }

            }
            //下
            next = cur;
            next._row += 1;
            if (CheckAccess(cur, next))
            {
                _maze[next._row][next._col] = _maze[cur._row][cur._col] + 1;
                if (GetPathR(next, path))
                {
                    return true;
                }

            }
            //左
            next = cur;
            next._col -= 1;
            if (CheckAccess(cur, next))
            {
                _maze[next._row][next._col] = _maze[cur._row][cur._col] + 1;
                if (GetPathR(next, path))
                {
                    return true;
                }

            }
            //右
            next = cur;
            next._col += 1;
            if (CheckAccess(cur, next))
            {
                _maze[next._row][next._col] = _maze[cur._row][cur._col] + 1;
                if (GetPathR(next, path))
                {
                    return true;
                }

            }

            //回溯
            return false;//返回上一层调用
        }
    }