MATLAB一维非线性方程 插值迭代方法

一般而言，方程没有能够普遍求解的silver bullet，但是有几类方程的求解方法已经非常清晰确凿了，比如线性方程、二次方程或一次分式。一次方程可以直接通过四则运算反解出答案，二次方程的求根公式也给出了只需要四则运算和开根号的符号表达式。而一次分式的分子即为一次函数。更多的方程并没有普适的符号表达式，但通过用便于求零点的函数模仿、代替之也可以估计零点的位置。插值方法可以实现这一思路。

　　插值迭代方法包括割线法、二次插值法等多项式插值方法，反插法以及线性分式插值法等等，其核心是用几个点及其函数值信息，通过插值产生一条容易计算零点的函数图线，然后用插值函数的零点来估计原函数的零点，不断迭代以达到足够的精度。每个算法的大致思路均相同，不再分别阐述具体原理。

1. 割线法(Secant Method)

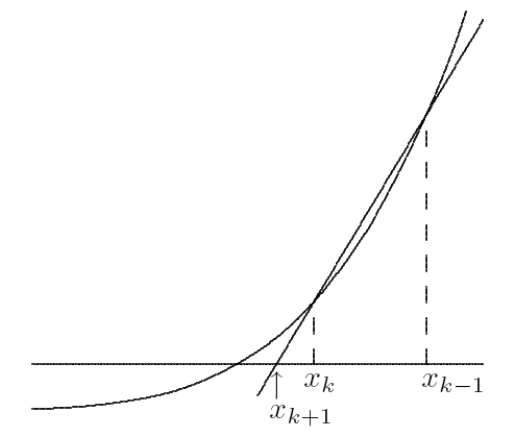
　　用一次函数模拟原函数，用该一次函数的零点作为原函数零点的下一个估计。起始需要两个点。迭代式：$$x_{k+1}=x_k-f(x_k)\frac{x_k-x_{k-1}}{f(x_k)-f(x_{k-1})}$$　　迭代式和牛顿法的迭代式类似。实际上，割线法正是用两点的割线斜率代替了牛顿法中使用的切线斜率（即导数）：$f'(x_k)\approx [f(x_k)-f(x_{k-1})]/(x_k-x_{k-1})$ .

function [ zeropt, iteration ] = SecantMethod( func, start0, start1, prec )
%　　割线法求零点，函数句柄func，两个起点start0,start1，绝对精度prec
%   返回：零点zeropt，迭代步数iteration
prev = start0;
current = start1;
next = current - func(current)*(current - prev)/(func(current) - func(prev));
iteration = 0;
while abs(next - current) > prec && iteration < 500
    prev = current;
    current = next;
    next = current - func(current)*(current - prev)/(func(current) - func(prev));