算法沉淀第四天（Winner）

原创于 2025-10-16 21:52:19 发布 · 1k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

算法专栏收录该内容

26 篇文章

订阅专栏

引言：

今天是算法沉淀的第四天，昨天我们沉淀了基础的位运算方面的题目，今天我们来沉淀CF的题，感觉分数限定完如果从后往前刷，每次都会有新题又出现在前面，看着不舒服，所以我决定从最早的题开始刷起，如图

我从最早的题开始刷起，这样就不会又跳出新题影响观感了，桀桀桀

那么，我们今天来讲一道CF评级为1500的题，就是上图AC的那题，话不多说，我们就进入今天的算法讲解———————>

Winner

按照惯例，我们先来看题目

题意分析

题目链接在这Problem - 2A - Codeforces

不想跳转的可看下图

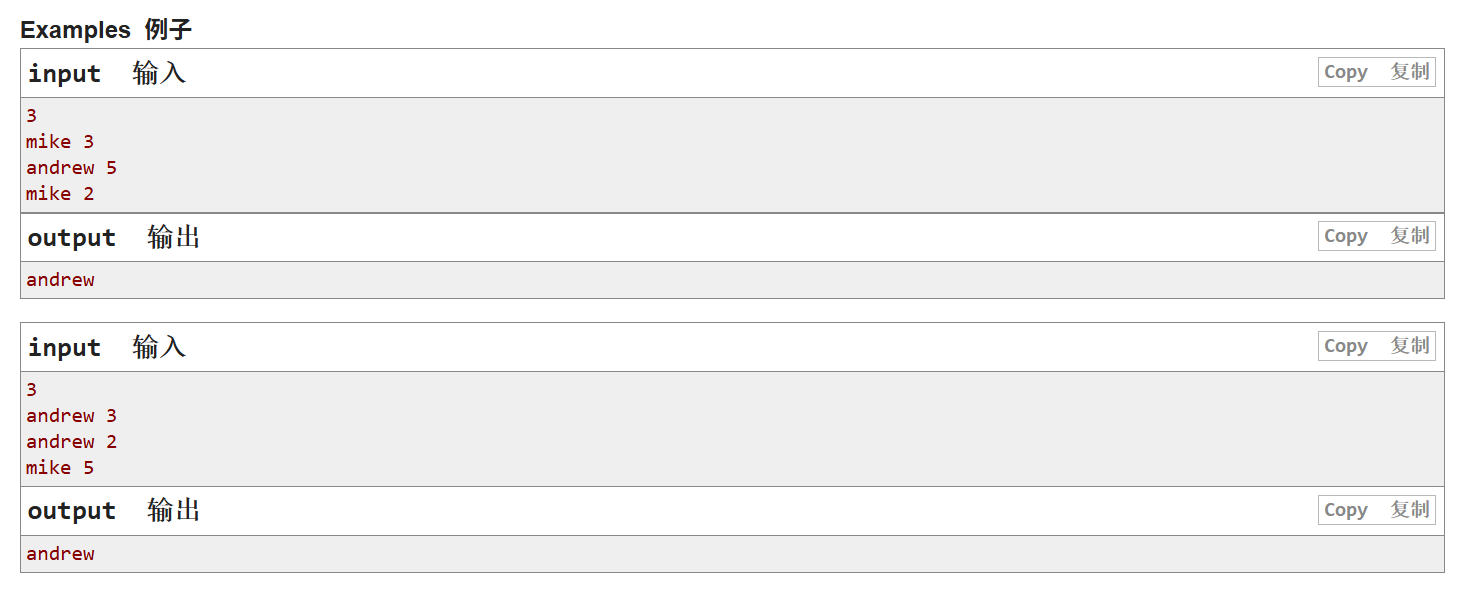
这一题的题目很简单，就是给你ｎ轮比拼，每轮都会告诉你一个人的分数变化了多少（其余人分数不变），然后ｎ轮全部结束后，问最终的获胜者是谁，输出获胜者的名字就可以啦

分数最高的获胜，这毋庸置疑，但是如果最后有多个人分数一样高，那么就要看这些人里哪个人是最先达到这个分数的，然后输出那个人的名字（这是最阴的）

那么，题目的意思和要求就分析完啦，接下来就进入逻辑梳理环节

逻辑梳理

这题如果去掉多人分数相同时那个获胜者的评判条件的话就会很简单，但是，这条件加上就会很阴了，需要多好多的代码来实现这个需求

因为数据范围十分的小（只有１ｅ３），所以我们可以尝试用暴力的方式来解决这个问题

首先我们要先解决怎么处理这些人的数据的存储和展示

这个其实很简单，只要用vector数组开一个string的数据类型就可以了，用这个数组来存每个名字，然后再开一个vector数组装int数据，用来存对应名字的分数

然后怎么对这俩个vector数组进行操作呢，很简单，每轮时候都先寻找一下装string的那个vector数组中有没有这个名字，如果没有就用将这个名字新加入数组中，然后再将他的分数加入数组中，因为这俩个信息都是同时开新位置的，所以这俩个数组的长度是一样的

这时候，又有问题了，那就是因为有俩种情况，直接循环找最大值肯定不现实

所以，我们可以用一个结构体数组来存相关数据（一个是名字对于数组的下标，还有一个是是这个名字对应的分数），然后每次循环的时候对这个结构体进行结构体排序（通过分数来进行排序，由大到小）

然后将排序完得到的第一个结构体元素和位置再传到新的结构体数组里，来表示进行不同轮数的时候的胜者是谁，并且胜者的分数是几分，这个对于遇到结束后有多个不同分数的情况下有用

接下来，前面的操作都铺垫完了，最后就是找胜者的过程了

首先判断是不是最大值只有一个

如果只有一个，直接输出最大的值对应的人名就可以了

如果有多个，那么就从第一轮开始循环，判断每一轮都第一的分数有没有到达最后的胜者分，如果到达了，就判断这个人是不是胜者名单里的人，如果是，那就输出这个人，结束循环就好了

那么，这道题的逻辑梳理就梳理完啦，接下来，我们就进入代码实现的环节

代码实现

那么，逻辑梳理已经把流程全说完啦，就直接给AC源码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;

int n;

struct node
{
	int wei;
	int weigh;
}T[1010];

struct Node
{
	int We;
	string A;
	int Weight;
}ans[1010];

bool cmp(node xx, node yy)
{
	return xx.weigh > yy.weigh;
}

int main()
{
	cin >> n;
	vector<string> a;
	vector<int>q;
	string b;
	int t;
	string d;
	for(int k = 1;k<=n;k++)
	{
		int Wei = 0;
		int xixi = 1;
		cin >> b >> t;
		for (int i = 0; i < a.size(); i++)
		{
			if (a[i].size() == b.size())
			{
				int xi = 1;
				for (int j = 0; j < b.size(); j++)
				{
					if (a[i][j] != b[j])
					{
						xi = 0;
						break;
					}
				}
				if (xi)
				{
					Wei = i;
					xixi = 0;
					q[i] += t;
				}
			}
		}
		if (xixi)
		{
			a.push_back(b);
			q.push_back(t);
			Wei = q.size() - 1;
			T[Wei].wei = Wei;
		}
		for (int i = 0; i < a.size(); i++)
		{
			if (Wei == T[i].wei)
				T[i].weigh = q[Wei];
		}
		sort(T, T + q.size(), cmp);
		d = a[T[0].wei];
		ans[k].A = d;
		ans[k].Weight = T[0].weigh;
		ans[k].We = T[0].wei;
	}
	if (T[0].weigh == T[1].weigh)
	{
		for (int k = 1; k <= n; k++)
		{
			if (ans[k].Weight >= T[0].weigh && T[0].weigh == q[ans[k].We])
			{
				cout << ans[k].A << endl;
				return 0;
			}
		}
	}
	else
		cout << d << endl;
	return 0;
}

那么，这题就讲解完啦