最短路径算法

        最短路径 是数学中的一类问题，常常在 奥数比赛、计算机竞赛等场合出没，对应现实生活的问题就是 找一个从A点到B点的最短路，其价值和意义很明显。

        常用的路径算法有：Dijkstra算法、A*算法、SPFA算法、动态规划法、Bellman-Ford算法和Floyd-Warshall算法 等等，这里我们只讲 最常用的Dijkstra算法。

Dijkstra算法：

        算法采用了贪心思想，即每次都查找与该点距离最近的点，其算法复杂度为 O(n^2)。

        定义S描述已完成规划点集，U表示未完成规划点集，v表示源顶点，那么算法步骤可以描述为：

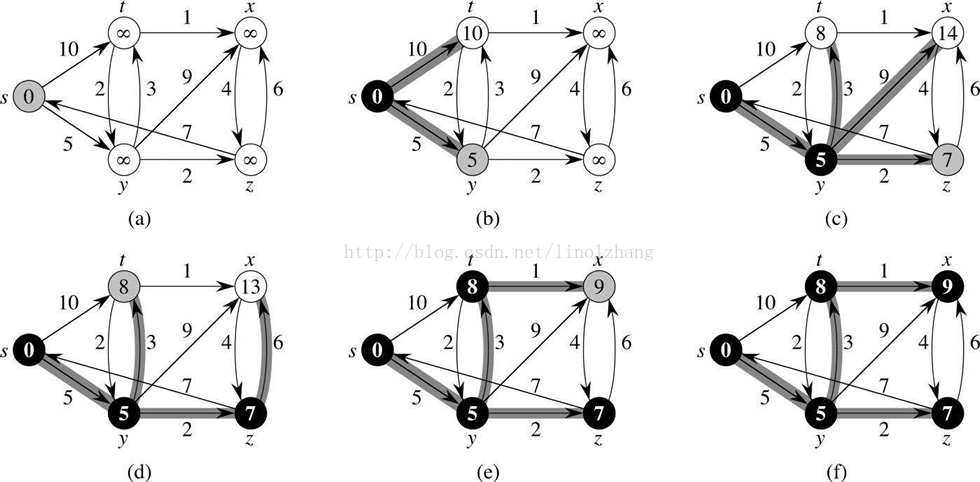
1. 初始化，S只含有源顶点v；

2. 从U中选取一个距离v最小的顶点k加入S中（该选定的距离就是v到k的最短路径长度）；

3. 以k为新考虑的中间点，修改U中各顶点的距离；若从源节点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值是顶点k的距离加上k到u的距离；

4. 重复步骤 2、3，直到所有顶点都包含在S中。

代码参考：

        头文件（SearchGraph.h）

/* SearchGraph类 - 最短路径搜索 
    linolzhang, 2009.6.22
*/
#include <vector>
#include <string>
#include <map>
#include <queue>
#include <functional>
#include <float.h>

// 边
struct Vertex;
struct Edge
{
	Vertex* src;    // s
	Vertex* dest;   // w
	float weight;

	Edge(Vertex* _src,Vertex* _dest,float w) : src(_src),dest(_dest),weight(w)
	{
	}
};
struct EdgeIndex  // 用于边索引查找
{
	std::string srcID;
	std::string destID;

	EdgeIndex(const std::string& _srcID,const std::string& _destID) : srcID(_srcID),destID(_destID)
	{
	}
	bool operator < (const EdgeIndex& rhs) const
	{  
		if(srcID != rhs.srcID)
			return srcID < rhs.srcID;

		return destID < rhs.destID;
	}
};
struct QNode  // 用于搜索
{   
	Vertex* vertex;
	float dist;

	QNode(Vertex* _vertex=NULL,float _dist=0.0f) : vertex(_vertex),dist(_dist)
	{
	}
	bool operator < (const QNode& rhs) const  {  return dist<rhs.dist; }
	bool operator > (const QNode& rhs) const  {  return dist>rhs.dist; }
};

// 每个顶点基本信息
struct Vertex
{
	std::string	ID;      // 顶点ID
	std::vector<Edge*> adjEdgeInList;   // 入边列表
	std::vector<Edge*> adjEdgeOutList;  // 出边列表

	float dist;    // 与目标点的最短距离
	Vertex* next;  // 记录到目标最短路径中的 下一个顶点
	bool bVisited; // 是否已访问

	Vertex(const std::string& id) : ID(id),dist(FLT_MAX),next(NULL),bVisited(false)
	{
	};

	void reset()
	{ 
		dist = FLT_MAX; next = NULL; bVisited = false;
	}
};

// 搜索图类，记录有向边集合，Djkstra算法搜索最短路径
class SearchGraph
{
public:
	SearchGraph(void);
	~SearchGraph(void);

	SearchGraph* clone();        // 克隆一个搜索图

public:
	Vertex* addVertex(const std::string& id);   // 添加顶点
	Vertex* getVertex(const std::string& id);   // 得到顶点
	void removeVertex(const std::string& id);   // 删除顶点，需要先删除其关联的边

	bool addEdge(const std::string& srcID,const std::string& destID,float weight);  // 添加边
	Edge* getEdge(const std::string& srcID,const std::string& destID);              // 得到边
	void removeEdge(const std::string& srcID,const std::string& destID);            // 删除边，首先解除与顶点的关联

	// djkstra算法搜索最短路
	bool getShortestPath(const std::string& vID,bool bFrom=true);    // bFrom ：从该点出发

protected:
	std::map<std::string,Vertex*> m_VertexList;   // 顶点列表
	std::map<EdgeIndex,Edge*> m_EdgeList;         // 边列表
};

        cpp文件（SearchGraph.cpp）

#include "SearchGraph.h"

SearchGraph::SearchGraph(void)
{
}

SearchGraph::~SearchGraph(void)
{
	// 删除顶点
	std::map<std::string,Vertex*>::iterator ite_v = m_VertexList.begin();
	for( ; ite_v != m_VertexList.end(); ++ite_v )
		delete ite_v->second;

	// 删除边
	std::map<EdgeIndex,Edge*>::iterator ite_e = m_EdgeList.begin();
	for( ; ite_e != m_EdgeList.end(); ++ite_e )
		delete ite_e->second;
}

// 克隆一个搜索图
SearchGraph* SearchGraph::clone()
{
	SearchGraph* newSearchGraph = new SearchGraph();

	// 复制Vertex
	std::map<std::string,Vertex*>::iterator ite_v = m_VertexList.begin();
	for( ; ite_v != m_VertexList.end(); ++ite_v )
	{
		newSearchGraph->addVertex(ite_v->first);
	}

	// 复制Edge
	std::map<EdgeIndex,Edge*>::iterator ite_e = m_EdgeList.begin();
	for( ; ite_e != m_EdgeList.end(); ++ite_e )
	{
		newSearchGraph->addEdge(ite_e->first.srcID,ite_e->first.destID,ite_e->second->weight);
	}

	return newSearchGraph;
}

/
// --------------------------------------------
// 添加顶点
Vertex* SearchGraph::addVertex(const std::string& id)
{
	// 首先查找顶点ID，是否存在
	std::map<std::string,Vertex*>::iterator ite = m_VertexList.find(id);
	if( ite != m_VertexList.end() )
	{
		Vertex* pVertex = ite->second;
		return pVertex;
	}
	else
	{
		Vertex* pVertex = new Vertex(id);
		m_VertexList[id] = pVertex;
		return pVertex;
	}
}
// 得到顶点
Vertex* SearchGraph::getVertex(const std::string& id)
{
	// 查找顶点
	std::map<std::string,Vertex*>::iterator ite = m_VertexList.find(id);
	if( ite != m_VertexList.end() )
	{
		Vertex* pVertex = ite->second;
		return pVertex;
	}
	return NULL;
}
// 删除顶点，需要先删除其关联的边
void SearchGraph::removeVertex(const std::string& id)
{
	// 首先查找顶点ID，是否存在
	std::map<std::string,Vertex*>::iterator ite = m_VertexList.find(id);
	if( ite != m_VertexList.end() )
	{
		Vertex* pVertex = ite->second;
		// 首先删除关联的边
		for(size_t i=0;i<pVertex->adjEdgeInList.size();i++)
		{
			removeEdge(pVertex->adjEdgeInList[i]->src->ID,pVertex->adjEdgeInList[i]->dest->ID);
		}
		for(size_t i=0;i<pVertex->adjEdgeOutList.size();i++)
		{
			removeEdge(pVertex->adjEdgeOutList[i]->src->ID,pVertex->adjEdgeOutList[i]->dest->ID);
		}
		// 删除顶点
		delete pVertex;
		m_VertexList.erase(ite);
	}
}

bool SearchGraph::addEdge(const std::string& srcID,const std::string& destID,float weight)
{
	Vertex* pSrc = addVertex(srcID);
	Vertex* pDest = addVertex(destID);

	// 查找是否已添加
	Edge* pEdge = getEdge(srcID,destID);
	if(pEdge)
		return false;

	// 建立新边
	pEdge = new Edge(pSrc,pDest,weight);
	m_EdgeList.insert( std::pair<EdgeIndex,Edge*>(EdgeIndex(srcID,destID),pEdge) );

	pSrc->adjEdgeOutList.push_back( pEdge );
	pDest->adjEdgeInList.push_back( pEdge );

	return true;
}

// 得到边
Edge* SearchGraph::getEdge(const std::string& srcID,const std::string& destID)
{
	EdgeIndex index(srcID,destID);

	// 查找边
	std::map<EdgeIndex,Edge*>::iterator ite = m_EdgeList.find(index);
	if( ite != m_EdgeList.end() )
	{
		Edge* pEdge = ite->second;
		return pEdge;
	}
	return NULL;
}
// 删除边，首先解除与顶点的关联
void SearchGraph::removeEdge(const std::string& srcID,const std::string& destID)
{
	EdgeIndex index(srcID,destID);

	// 查找边
	std::map<EdgeIndex,Edge*>::iterator ite = m_EdgeList.find(index);
	if( ite != m_EdgeList.end() )
	{
		Edge* pEdge = ite->second;

		// 首先解除与顶点的关联
		std::vector<Edge*>::iterator ite1 = pEdge->src->adjEdgeOutList.begin();
		for( ; ite1!=pEdge->src->adjEdgeOutList.end(); ++ite1 )
		{
			if( *ite1 == pEdge )
				pEdge->src->adjEdgeOutList.erase(ite1);  // 移除邻接边 - 出边
		}
		std::vector<Edge*>::iterator ite2 = pEdge->dest->adjEdgeInList.begin();
		for( ; ite2!=pEdge->dest->adjEdgeInList.end(); ++ite2 )
		{
			if( *ite2 == pEdge )
				pEdge->dest->adjEdgeInList.erase(ite2);  // 移除邻接边 - 入边
		}

		// 删除边
		delete pEdge;
		m_EdgeList.erase(ite);
	}
}

// djkstra算法搜索最短路 - bFrom：从该点出发
bool SearchGraph::getShortestPath(const std::string& vID,bool bFrom)
{
	// 顶点是否存在 ？
	std::map<std::string,Vertex*>::iterator ite = m_VertexList.find(vID);
	if( ite == m_VertexList.end() )
		return false;

	Vertex* startVertex = ite->second;

	//  重置搜索图，清空标记
	ite = m_VertexList.begin();
	for( ; ite!=m_VertexList.end(); ++ite )
		ite->second->reset();

	// 定义优先队列，greater最小堆 - 默认是最大堆less
	std::priority_queue< QNode,std::vector<QNode>,std::greater<QNode> > q;

	// 初始化，添加启始搜索顶点
	startVertex->dist = 0;
	QNode startNode(startVertex,0);  // 初始节点，dist置0
	q.push(startNode);

	// ------------------------------------------
	// 遍历
	QNode currNode;    // 当前遍历到的节点
	while(!q.empty())
	{
		// 弹出栈顶最大 Dist 的节点
		currNode = q.top();  q.pop();

		// 过滤已访问过的情况
		if(currNode.vertex->bVisited)
			continue;
		currNode.vertex->bVisited = true;

		// 搜索方向控制
		size_t adjEdgeCount = 0;  // 邻接边数
		if(bFrom)  // 搜索点作为起始点
			adjEdgeCount = currNode.vertex->adjEdgeOutList.size();
		else       // 搜索点作为终止点
			adjEdgeCount = currNode.vertex->adjEdgeInList.size();

		// 遍历邻接边
		for( size_t i=0; i<adjEdgeCount; i++ )
		{
			Edge* pEdge;
			Vertex* pNextVertex;
			if(bFrom)
			{
				pEdge = currNode.vertex->adjEdgeOutList[i];  // 出边
				pNextVertex = pEdge->dest;
			}
			else
			{
				pEdge = currNode.vertex->adjEdgeInList[i];   // 入边
				pNextVertex = pEdge->src;
			}
			// 过滤已访问过的情况 - 不加也可以，通过距离判断
			if(pNextVertex->bVisited)
				continue;
	
			// 如果 目标顶点 到 开始顶点 的距离 大于
			// 以 当前节点 为中介的路径长度（当前节点dist+边weight），需要更新最短路
			if( pNextVertex->dist > currNode.dist+pEdge->weight )
			{
				pNextVertex->dist = currNode.dist + pEdge->weight;
				pNextVertex->next = currNode.vertex;  // 记录前驱
				q.push( QNode(pNextVertex,pNextVertex->dist) );
			}
		}
	}

	// 搜索完成，返回
	return true;
}