Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematic

Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematics Geometry History and Terminology Number Theory Probability and Statistics Recreational Mathematics Topology Alphabetical Index Interactive Entries Random Entry New in MathWorld MathWorld Classroom About MathWorld Contribute to MathWorld Send a Message to the Team MathWorld Book Wolfram Web Resources » 13,172 entries Last updated: Mon Jul 29 2013 Created, developed, and nurtured by Eric Weissteinat Wolfram Research

Geometry > Plane Geometry > Circles > Geometry > Curves > Plane Curves > Conic Sections > Geometry > Curves > Plane Curves > Polar Curves > More...   Ci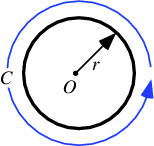rcle   A circle is the set of points in a plane that are equidistant from a given point . The distance  from the center is called the radius, and the point  is called the center. Twice the radius is known as the diameter . The angle a circle subtends from its center is a full angle, equal to  or  radians. A circle has the maximum possible area for a given perimeter, and the minimum possible perimeter for a given area. The perimeter  of a circle is called the circumference, and is given by (1) This can be computed using calculus using the formula for arc length in polar coordinates, (2) but since , this becomes simply (3) The circumference-to-diameter ratio 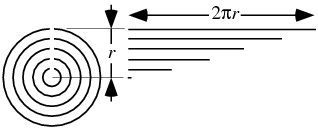 for a circle is constant as the size of the circle is changed (as it must be since scaling a plane figure by a factor increases its perimeter by ), and  also scales by . This ratio is denoted  (pi), and has been proved transcendental. Knowing , the area of the circle can be computed either geometrically or using calculus. As the number of concentric strips increases to infinity as illustrated above, they form a triangle, so (4) This derivation was first recorded by Archimedes in Measurement of a Circle (ca. 225 BC). 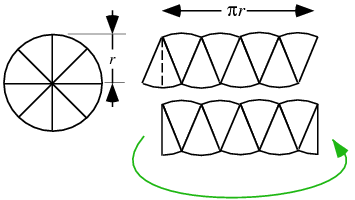If the circle is instead cut into wedges, as the number of wedges increases to infinity, a rectangle results, so (5) From calculus, the area follows immediately from the formula (6) again using polar coordinates. A circle can also be viewed as the limiting case of a regular polygon with inradius  and circumradius  as the number of sides  approaches infinity (a figure technically known as an apeirogon). This then gives the circumference as (7) (8) and the area as (9) (10) which are equivalently since the radii  and  converge to the same radius as . Unfortunately, geometers and topologists adopt incompatible conventions for the meaning of "-sphere," with geometers referring to the number of coordinates in the underlying space and topologists referring to the dimension of the surface itself (Coxeter 1973, p. 125). As a result, geometers call the circumference of the usual circle the 2-sphere, while topologists refer to it as the 1-sphere and denote it . The circle is a conic section obtained by the intersection of a cone with a plane perpendicular to the cone's symmetry axis. It is also a Lissajous curve. A circle is the degenerate case of an ellipse with equal semimajor and semiminor axes (i.e., with eccentricity 0). The interior of a circle is called a disk. The generalization of a circle to three dimensions is called a sphere, and to  dimensions for  a hypersphere. The region of intersection of two circles is called a lens. The region of intersection of three symmetrically placed circles (as in a Venn diagram), in the special case of the center of each being located at the intersection of the other two, is called a Reuleaux triangle. In Cartesian coordinates, the equation of a circle of radius  centered on  is (11) In pedal coordinates with the pedal point at the center, the equation is (12) The circle having  as a diameter is given by (13) The parametric equations for a circle of radius  can be given by (14) (15) The circle can also be parameterized by the rational functions (16) (17) but an elliptic curve cannot. 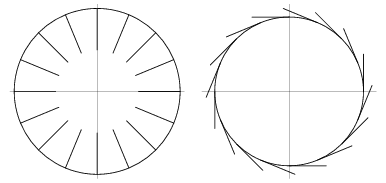The plots above show a sequence of normal and tangent vectors for the circle. The arc length , curvature , and tangential angle  of the circle with radius  represented parametrically by (◇) and (◇) are (18) (19) (20) The Cesàro equation is (21) In polar coordinates, the equation of the circle has a particularly simple form. (22) is a circle of radius  centered at origin, (23) is circle of radius  centered at , and (24) is a circle of radius  centered on . The equation of a circle passing through the three points  for , 2, 3 (the circumcircle of the triangle determined by the points) is (25) The center and radius of this circle can be identified by assigning coefficients of a quadratic curve (26) where  and  (since there is no  cross term). Completing the square gives (27) The center can then be identified as (28) (29) and the radius as (30) where (31) (32) (33) (34) Four or more points which lie on a circle are said to be concyclic. Three points are trivially concyclic since three noncollinear points determine a circle. In trilinear coordinates, every circle has an equation of the form (35) with  (Kimberling 1998, p. 219). The center  of a circle given by equation (35) is given by (36) (37) (38) (Kimberling 1998, p. 222). In exact trilinear coordinates , the equation of the circle passing through three noncollinear points with exact trilinear coordinates , , and  is (39) (Kimberling 1998, p. 222). An equation for the trilinear circle of radius  with center  is given by Kimberling (1998, p. 223). SEE ALSO:Adams' Circle, Apeirogon, Arc, Blaschke's Theorem, Brahmagupta's Formula, Brocard Circle, Casey's Theorem, Central Circle, Cevian Circle, Chord, Circle Evolute, Circle Inscribing, Circle Involute, Circle-Line Intersection, Circle Parallel Curves, Circle Power, Circumcircle, Circumference, Clifford's Circle Theorem, Closed Disk, Concentric Circles, Cosine Circle, Cotes Circle Property, Diameter, Disk, Droz-Farny Circles, Ellipse, Euler Triangle Formula,Excircles, Excosine Circle, Eyeball Theorem, Feuerbach's Theorem, First Lemoine Circle, Five Disks Problem, Flower of Life, Ford Circle, Fuhrmann Circle,Gershgorin Circle Theorem, Hart Circle, Incircle, Inversive Distance, Kinney's Set, Lens, Lester Circle, Lissajous Curve, Magic Circles, Malfatti Circles, McCay Circles, Midcircle, Miquel Five Circles Theorem, Monge's Circle Theorem, Neuberg Circles, Nine-Point Circle, Open Disk, Parry Circle, Pi, Point Circle, Polar Circle, Prime Circle, Pseudocircle, Ptolemy's Theorem, Purser's Theorem, Radical Line, Radius, Reuleaux Triangle, Seed of Life, Seifert Circle, Semicircle,Seven Circles Theorem, Similitude Circle, Squircle, Six Circles Theorem, Soddy Circles, Sphere, Spieker Circle, Taylor Circle, Tucker Circles, Unit Circle,Venn Diagram, Villarceau Circles, Yin-Yang REFERENCES: Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 125 and 197, 1987. Casey, J. "The Circle." Ch. 3 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 96-150, 1893. Coolidge, J. L. A Treatise on the Geometry of the Circle and Sphere. New York: Chelsea, 1971. Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 74-75, 1996. Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. Coxeter, H. S. M. and Greitzer, S. L. "Some Properties of the Circle." Ch. 2 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 27-50, 1967. Dunham, W. "Archimedes' Determination of Circular Area." Ch. 4 in Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 84-112, 1990. Eppstein, D. "Circles and Spheres." http://www.ics.uci.edu/~eppstein/junkyard/sphere.html. Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 1, 1999. Kern, W. F. and Bland, J. R. Solid Mensuration with Proofs, 2nd ed. New York: Wiley, p. 3, 1948. Kimberling, C. "Triangle Centers and Central Triangles." Congr. Numer. 129, 1-295, 1998. Lachlan, R. "The Circle." Ch. 10 in An Elementary Treatise on Modern Pure Geometry. London: Macmillian, pp. 148-173, 1893. Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 65-66, 1972. MacTutor History of Mathematics Archive. "Circle." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Circle.html. Pappas, T. "Infinity & the Circle" and "Japanese Calculus." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 68 and 139, 1989. Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., 1995. Yates, R. C. "The Circle." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 21-25, 1952. CITE THIS AS: Weisstein, Eric W. "Circle." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Circle.html Wolfram Web Resources Mathematica » The #1 tool for creating Demonstrations and anything technical. Wolfram|Alpha » Explore anything with the first computational knowledge engine. Wolfram Demonstrations Project » Explore thousands of free applications across science, mathematics, engineering, technology, business, art, finance, social sciences, and more. Computable Document Format » The format that makes Demonstrations (and any information) easy to share and interact with. STEM initiative » Programs & resources for educators, schools & students. Computerbasedmath.org » Join the initiative for modernizing math education.  Contact the MathWorld Team © 1999-2013 Wolfram Research, Inc. | Terms of Use

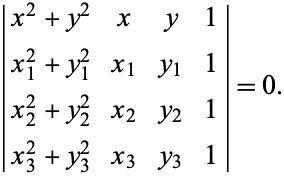
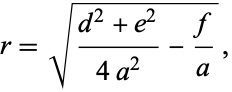
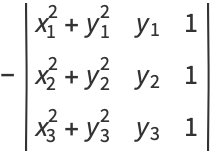
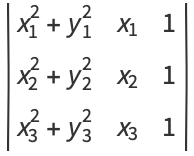
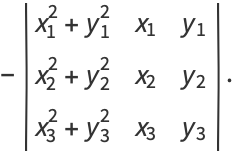
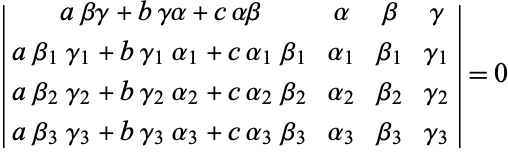
THINGS TO TRY: circle 5th hexagonal number code 506119 k=4 Area between a Line and the Graph of a Function Abraham Gadalla How Area Changes with Diameter Sarah Lichtblau Problems on Circles XIII: Common Area of Two Circles Jaime Rangel-Mondragon Problems on Circles X: Tangent Circles Generate Ellipses Jaime Rangel-Mondragon