用贝叶斯分类器进行简单天气预测

一、引言

在机器学习和数据科学中，分类问题一直是一个重要的研究领域。贝叶斯分类器作为一种基于贝叶斯定理的分类方法，在文本分类、垃圾邮件过滤、情感分析等领域得到了广泛的应用。本文将详细介绍贝叶斯分类器的原理、公式、先验概率、条件概率和后验概率等核心概念。

二、贝叶斯定理

贝叶斯定理是概率论中的一个基本定理，用于描述两个事件之间的条件概率关系。在贝叶斯分类器中，它用于计算给定特征下某个类别的后验概率。

贝叶斯定理的公式如下：

其中：

• ( P(A|B) ) 是事件A在事件B发生的条件下的概率，即后验概率。
• ( P(B|A) ) 是事件B在事件A发生的条件下的概率，即条件概率。
• ( P(A) ) 是事件A发生的概率，即先验概率。
• ( P(B) ) 是事件B发生的概率。

在分类问题中，事件A通常表示某个类别，事件B表示某个特征或特征组合。

三、贝叶斯分类器原理

贝叶斯分类器基于贝叶斯定理和特征条件独立性假设进行分类。它假设输入特征在给定类别下是条件独立的，即一个特征的出现概率不依赖于其他特征的出现概率。这个假设大大简化了计算，使得贝叶斯分类器在实际应用中非常高效。

在分类问题中，我们通常需要计算给定特征下每个类别的后验概率，然后选择后验概率最大的类别作为预测结果。根据贝叶斯定理，我们可以将后验概率表示为：

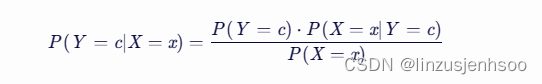
但是，由于我们在计算过程中并不直接需要 P(X=x)（因为我们只是比较不同类别的后验概率而 P(X=x) 对于所有类别都是相同的），所以我们通常只计算分子部分：

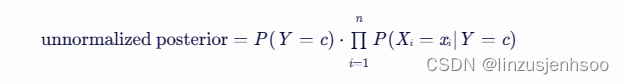
四、先验概率、条件概率和后验概率

• 先验概率（Prior Probability）：在没有任何其他信息的情况下，某个类别或事件发生的概率。在贝叶斯分类器中，先验概率通常通过统计训练数据集中各类别的出现频率来估计。

• 条件概率（Conditional Probability）：一个事件在另一个事件发生的条件下的概率。在贝叶斯分类器中，条件概率表示在给定类别下某个特征或特征组合的出现概率。这些概率通常通过统计训练数据集中每个类别下特征的出现频率来估计。

• 后验概率（Posterior Probability）：在给定某些信息或证据后，某个类别或事件发生的概率。在贝叶斯分类器中，后验概率表示在给定特征下某个类别的概率。后验概率是通过贝叶斯定理和先验概率、条件概率计算得到的。

五、应用示例

以天气预测为例，假设我们知道一些已知情况下的天气情况，需要根据已知条件判断其不同天气的概率。我们可以将天气内容转化为一系列特征，并使用贝叶斯分类器进行分类。通过计算不同天气的先验概率以及每个类别下各个特征的条件概率，我们可以计算给定情况下后验概率，并据此进行预测。

1. 数据准备

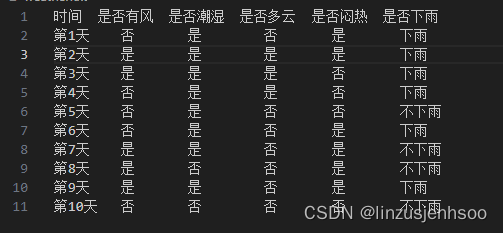
首先，我们需要准备一些天气相关的数据。这里我们使用了一个简单的数据集，其中包含天气特征和对应的标签（是否下雨）。

 样本：

代码：

import numpy as np  
from collections import Counter  
  
# 给定的数据  
x = np.array([  
    [0, 1, 0, 1],  
    [1, 1, 1, 1],  
    # ... 其他数据点  
    [0, 0, 0, 0]  
])  
y = np.array([1, 1, 1, 1, 0, 1, 0, 0, 1, 0])

其中，x 是一个二维数组，每一行代表一个天气特征向量（例如，不同的天气指标），y 是一个一维数组，代表每个天气特征向量对应的标签（1 表示下雨，0 表示不下雨）。

2. 计算先验概率

先验概率是指在没有任何其他信息的情况下，某个事件发生的概率。在这个例子中，先验概率就是下雨或不下雨的概率。

# 计算先验概率 
n_samples = len(y) 
prior_rain = np.sum(y == 1) / n_samples 
prior_no_rain = 1 - prior_rain 


print(f"先验概率（下雨）: {prior_rain}") 
print(f"先验概率（不下雨）: {prior_no_rain}")

 

3. 计算条件概率

条件概率是指在某个事件已经发生的条件下，另一个事件发生的概率。在这个例子中，我们需要计算在下雨或不下雨的条件下，每个特征取值为0或1的概率。

# 计算条件概率 
n_features = x.shape[1] 
conditional_probs_rain = np.zeros((n_features, 2)) # [特征, [0的概率, 1的概率]] 
conditional_probs_no_rain = np.zeros((n_features, 2)) 


for feature_idx in range(n_features): 
# 当下雨时，特征为0和1的概率 
rain_feature_counts = Counter(x[y == 1, feature_idx]) 
conditional_probs_rain[feature_idx] = [ 
(rain_feature_counts[0] + 1) / (np.sum(y == 1) + 2), # 拉普拉斯平滑 
(rain_feature_counts[1] + 1) / (np.sum(y == 1) + 2) 
] 


# 当不下雨时，特征为0和1的概率 
no_rain_feature_counts = Counter(x[y == 0, feature_idx]) 
conditional_probs_no_rain[feature_idx] = [ 
(no_rain_feature_counts[0] + 1) / (n_samples - np.sum(y == 1) + 2), 
(no_rain_feature_counts[1] + 1) / (n_samples - np.sum(y == 1) + 2) 
] 


# 可以在这里打印条件概率以验证结果 
# ...

注意，我们使用了拉普拉斯平滑（Laplace smoothing）来处理零概率问题，确保条件概率总是非零的。

4. 计算后验概率

后验概率是在观察到新的证据后，某个假设成立的概率。在这个例子中，我们要计算给定一个新的天气特征向量时，下雨或不下雨的概率。

new_point = np.array([0, 1, 0, 1])

# 计算下雨的后验概率（未归一化）
posterior_rain = prior_rain
for feature_idx, feature_value in enumerate(new_point):
    posterior_rain *= conditional_probs_rain[feature_idx, feature_value]

# 如果需要，也可以计算不下雨的后验概率（未归一化）
posterior_no_rain = prior_no_rain
for feature_idx, feature_value in enumerate(new_point):
    posterior_no_rain *= conditional_probs_no_rain[feature_idx, feature_value]

# 输出结果（可选的归一化）
print(f"未归一化的下雨后验概率: {posterior_rain}")
print(f"未归一化的不下雨后验概率: {posterior_no_rain}")

5. 完整代码

import numpy as np
from collections import Counter

# 给定的数据
x = np.array([
    [0, 1, 0, 1],
    [1, 1, 1, 1],
    [1, 1, 1, 0],
    [0, 1, 1, 0],
    [0, 1, 0, 0],
    [0, 1, 0, 1],
    [1, 1, 0, 1],
    [1, 0, 0, 1],
    [1, 1, 0, 1],
    [0, 0, 0, 0]
])
y = np.array([1, 1, 1, 1, 0, 1, 0, 0, 1, 0])

# 计算先验概率
n_samples = len(y)
prior_rain = np.sum(y == 1) / n_samples
prior_no_rain = 1 - prior_rain

# 计算条件概率
n_features = x.shape[1]
conditional_probs_rain = np.zeros((n_features, 2))  # [特征, [0的概率, 1的概率]]
conditional_probs_no_rain = np.zeros((n_features, 2))

for feature_idx in range(n_features):
    # 当下雨时，特征为0和1的概率
    rain_feature_counts = Counter(x[y == 1, feature_idx])
    conditional_probs_rain[feature_idx] = [
        (rain_feature_counts[0] + 1) / (np.sum(y == 1) + 2),  # 拉普拉斯平滑
        (rain_feature_counts[1] + 1) / (np.sum(y == 1) + 2)
    ]

    # 当不下雨时，特征为0和1的概率
    no_rain_feature_counts = Counter(x[y == 0, feature_idx])
    conditional_probs_no_rain[feature_idx] = [
        (no_rain_feature_counts[0] + 1) / (n_samples - np.sum(y == 1) + 2),
        (no_rain_feature_counts[1] + 1) / (n_samples - np.sum(y == 1) + 2)
    ]

# 预测新数据点的后验概率（这里假设新数据点是 [0, 1, 0, 1]）
new_point = np.array([0, 1, 0, 1])

# 计算下雨的后验概率（未归一化）
posterior_rain = prior_rain
for feature_idx, feature_value in enumerate(new_point):
    posterior_rain *= conditional_probs_rain[feature_idx, feature_value]

# 如果需要，也可以计算不下雨的后验概率（未归一化）
posterior_no_rain = prior_no_rain
for feature_idx, feature_value in enumerate(new_point):
    posterior_no_rain *= conditional_probs_no_rain[feature_idx, feature_value]

6. 运行结果

7.对运行结果的分析

先验概率：
prior_rain：这是下雨的先验概率，即在整个数据集中下雨的比例。
prior_no_rain：这是不下雨的先验概率，即在整个数据集中不下雨的比例。这两个概率之和应该为1。

后验概率：
对于给定的新数据点 new_point，代码计算了下雨的后验概率 posterior_rain。这个后验概率是基于先验概率和条件概率计算得出的，它表示在给定新数据点的特征下，下雨的可能性。
归一化：
值得注意的是，代码中的后验概率计算是未归一化的。这意味着 posterior_rain 和 posterior_no_rain（如果计算了的话）之和可能不等于1。在实际应用中，通常会将后验概率归一化，以确保它们的和为1，但这并不影响分类决策，因为我们只关心相对大小。
改进点：
代码中只计算了下雨的后验概率，没有直接给出分类结果。可以通过比较下雨和不下雨的后验概率来确定最终的分类。

六、总结

贝叶斯分类器是一种基于贝叶斯定理和特征条件独立性假设的分类方法。它通过计算给定特征下每个类别的后验概率来进行分类，具有高效、易于实现等优点。在实际应用中，贝叶斯分类器被广泛应用于文本分类、垃圾邮件过滤、情感分析等领域。