八数码问题-A*(AStar)算法实现

置顶 BrokenGeeker

已于 2024-01-13 19:54:26 修改

阅读量5.6w

点赞数 79

文章标签：八数码问题 A*算法人工智能 AStar 8-puzzle

于 2018-03-28 19:18:13 首次发布

本文链接：https://blog.csdn.net/lishang6257/article/details/79732420

版权

C++ 同时被 2 个专栏收录

12 篇文章

订阅专栏

算法

1 篇文章

订阅专栏

本文深入解析A*算法原理及其在八数码问题中的应用，介绍启发式函数设计、open与close表维护，并提供代码实现，帮助读者掌握A*算法精髓。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

A*算法

A*算法

1 前言

$\qquad$ 八数码问题可以说得上是搜索问题中比较经典的，可以有很多种搜索策略，比如说有最常见的BFS，DFS，此外，A也是一个比较普遍的搜索算法。在八数码问题A往往可以得到最优的求解路径。（再也不用担心不会拼图了，哈哈哈

插播个文章推广，喜欢搜索话题可以订阅基于博弈树的开源五子棋AI教程及源码分享，里面详细的介绍了如何从零打造一个可玩性较高的五子棋AI，以及整个项目源码的分享

2 简介

$\qquad$ 可能还有很多没有对A很深的理解，以下是自己的一些小看法。
$\qquad$ A算法作为启发式搜索的一种，第一个必不可少是启发式函数；同时作为A*算法的比较显著的一个特点就是对open表和close表的维护.

2.1 启发式函数

$\qquad$ 启发式函数为f(n) = g(n) + h(n)
其中F为Final Score，代表A*算法衡量该节点最终值。G为Goal，计算了从起始节点到该节点的实际消耗。H为Heuristic Score，预估了当前节点到目标节点的消耗。
$\qquad$ 启发式函数听起来很有学问，其实可以很简单的理解为从源点到目标的所需要消耗的总代价f(n)（和适应度函数比较相像），这个总代价可以分成两个部分从源点到中间节点（搜索的中间状态）已经消耗的实际代价g（n），另一个部分就是对从中间节点到目标的预测h(n)。
$\qquad$ 通常来说，这里的代价一般是指各种距离，像欧式距离，曼哈顿距离等等，这个根据你所求解的实际问题决定。
$\qquad$ 另一个值得指出的就是预测，预测值直接影响了问题求解的效率以及能否求得合理的解。这里给出一个结论：对于任意预测值h(n）均小于等于实际值的话，我们可以说最终解就是问题的最优解。

2.2 open表与close表的维护

open表：先可以简单认为是一个未搜索节点的表
close表：先可以简单认为是一个已完成搜索的节点的表（即已经将下一个状态放入open表内）
$\qquad$ 规则一：对于新添加的节点S（open表和close表中均没有这个状态），S直接添加到open表中
$\qquad$ 规则二：对于已经添加的节点S（open表中并且close表中没有这个状态），若在open表中，与原来的状态 $S_{0}$ 的f(n)比较，取最小的一个。
$\qquad$ 规则三：下一个搜索节点的选择问题，选取open表中f(n)的值最小的状态作为下一个待搜索节点
$\qquad$ 规则四：每次需要将带搜索的节点下一个所有的状态按照规则一二更新open表,close表，搜索完该节点后，移到close表中。

2.3 算法

初始化：将起始节点添加到开放列表中。
循环执行以下步骤：
1 从开放列表中找出F评分最低的节点，将其设为当前节点。
2 检查当前节点是否是目标节点。如果是，则算法结束，路径被找到。
3 将当前节点移至关闭列表，并处理所有邻近节点：
4 如果邻近节点不在开放列表中，计算其G、H和F值，然后将其添加到开放列表。
5 如果邻近节点已在开放列表中，检查通过当前节点到达它的路径是否更好。如果更好，更新其F、G和H值。

2.4 实例演示

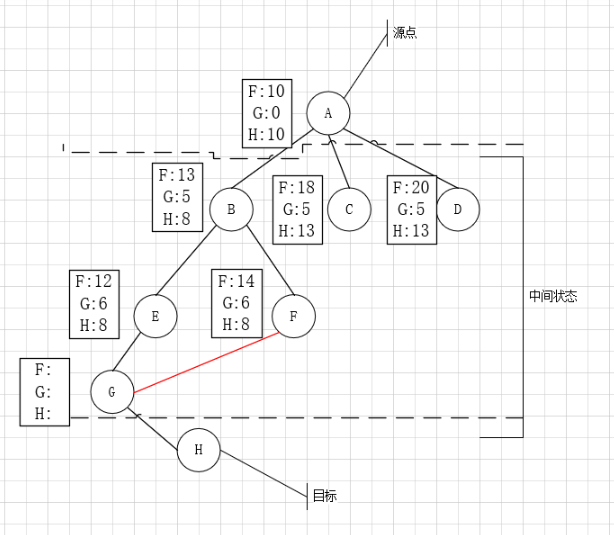
按照上述规则我们来体验一次简单的A*算法

A添加到open表中，更新A的f(n)为10
open 表：A(10)
close表：null
将B,C,D按照规则一添加到open表中，更新好B,C,D的f（n）后，将A移到close表中
open 表：B(13) C(18) D(20)
close表：A(10)
依据规则三，选取节点B作为下一个节点，同理将E,F移到open表，B移到close表
open 表：C(18) D(20) E(12) F(14)
close表：A(10) B(13)
依据规则三，选取E作为下一个节点，同理将G移到open表，E移到close表
open 表：C(18) D(20) F(14) G(15)
close表：A(10) B(13) E(12)
依据规则三，选取F作为下一个节点，按照规则二G(13) < G(15) 更新open表中的G。F移到close表
open 表：C(18) D(20) G(13)
close表：A(10) B(13) E(12) F(14)
继续搜索直至发现目标状态f（n）为open表中最小值

3 八数码问题

这里需要说明的A能找到的解是局部最优解，但是独特的启发式函数可以使得解为全局最优解，八数码问题就是一个能通过A求得最优解的问题。
像下图所示，通过将数字位向空格位移动直至将棋盘从初始状态变化到目标状态。

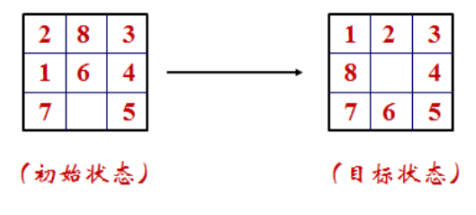
4 问题分析

启发式函数的确定
h(n):已经移动的步数
g(n):此状态与目标状态九宫格中相异数字的个数
状态保存
$\qquad$ A*算法有个很大的问题就是消耗内存资源，我们可以用char型数据保存，这里我另一种保存策略：用一个long int数值表示，方法如下
0-8九个状态可以四位二进制数来表示0000B-1000B,所以九个状态就可以用36个二进制位来表示，然后这36位二进制数就可以用一个long int型数据来表示，这样增加编码和解码工作，不过操作很风骚，位运算很好实现，只是这是后来想到的，没有实现
算法优化
$\qquad$ 在找最小值的时候，我们可以用二分查找，o(n)优化到o(logn)，这就要求我们再插入时顺序插入，因为查询次数是要大于添加open\close表项的，所以这个方法是可以优化执行效率的
无解情况
$\qquad$ 将九宫格变成线性后，计算初始状态和目标状态的奇偶性是否一致，一致有解，否则无解。

5 代码实现

原始代码实现

5.1 原始代码

#include <iostream>
#include <vector>
#include <ctime>
#include <cstdlib>
#define maxState 10000
#define N 3
using namespace std;


//判定状态b是否与状态空间下标为n的相同
bool isEqual(int stateSpace[N][N][maxState],int stateB[N][N],int n)
{
    for(int i = 0;i < N;i ++){
        for(int j = 0;j < N;j ++){
            if(stateSpace[i][j][n] != stateB[i][j]) return false;
        }
    }
    return true;
}

//判定状态b是否与状态a相同
bool isEqual(int stateA[N][N],int stateB[N][N])
{
    for(int i = 0;i < N;i ++){
        for(int j = 0;j < N;j ++){
            if(stateA[i][j] != stateB[i][j]) return false;
        }
    }
    return true;
}

//启发估计，就是求start->target的H值过程
int evalute(int start[N][N],int target[N][N])
{
    int num = 0;
    for(int i = 0;i < N;i ++){
        for(int j = 0;j < N;j ++)
            if(start[i][j] != target[i][j]) num ++;
    }
    return num;
}

//状态转移函数
//stateA中的空位经dir方向的唯一得到stateB
bool move(int stateA[N][N],int stateB[N][N],int dir)
{
    //1 up 2 down 3 left 4 right
    int x = 0,y = 0;
    for(int i = 0;i < N;i ++){
        for(int j = 0;j < N;j ++){
            stateB[i][j] = stateA[i][j];
            if(stateA[i][j] == 0) {
                x = i;y = j;
            }
        }
    }
    if(x == 0 && dir == 1) return false;
    if(x == N-1 && dir == 2) return false;
    if(y == 0 && dir == 3) return false;
    if(y == N-1 && dir == 4) return false;
    if(dir == 1){stateB[x-1][y] = 0;stateB[x][y] = stateA[x-1][y];}
    else if(dir == 2){stateB[x+1][y] = 0;stateB[x][y] = stateA[x+1][y];}
    else if(dir == 3){stateB[x][y-1] = 0;stateB[x][y] = stateA[x][y-1];}
    else if(dir == 4){stateB[x][y+1] = 0;stateB[x][y] = stateA[x][y+1];}
    else return false;
    return true;
}
//状态追加函数
//stateA保存在状态空间下标为n的位置
void appendState(int stateSpace[N][N][maxState],int stateA[N][N],int n)
{
    for(int i = 0;i < N;i ++){
        for(int j = 0;j < N;j ++){
            stateSpace[i][j][n] = stateA[i][j];
        }
    }
}
//状态提取函数
//提取状态空间下标为n的位置保存在stateA
void getState(int stateSpace[N][N][maxState],int stateA[N][N],int n)
{
    for(int i = 0;i < N;i ++){
        for(int j = 0;j < N;j ++){
            stateA[i][j] = stateSpace[i][j][n];
        }
    }
}
//状态拷贝函数
//提取状态B保存在stateA
void statecpy(int stateA[N][N],int stateB[N][N])
{
    for(int i = 0;i < N;i++){
        for(int j = 0;j < N;j++)
            stateA[i][j] = stateB[i][j];
    }
}
//状态查找函数
//查询状态A保存在状态空间中
int findState(int stateSpace[N][N][maxState],int stateA[N][N],int n)
{
    for(int i = 0;i < n;i ++){
        if(isEqual(stateSpace,stateA,i)) return i;
    }
    return -1;
}

int Astar(int stateSpace[N][N][maxState],int start[N][N],int target[N][N],int path[maxState])
{
    //初始化open,close表 openCloseList值为True时代表close表项，否则为open表项
    bool openCloseList[maxState] = {false};
    int FScore[maxState] = {0};
    int GScore[maxState] = {0};
    int curState[N][N];
    statecpy(curState,start);
    int id = 0,Curid = 0;
    FScore[id] = evalute(curState,target);
    appendState(stateSpace,start,id++);
    while(!isEqual(curState,target)){
        for(int i = 1;i < 5;i ++){//向四周找方向
            int tmp[N][N] = {{0}};
            if(move(curState,tmp,i)){
                int state = findState(stateSpace,tmp,id);
                if(state == -1){
                    //open表和close表中均无该项
                    path[id] = Curid;
                    GScore[id] = GScore[Curid] + 1;
                    FScore[id] = evalute(tmp,target) + GScore[id];
                    appendState(stateSpace,tmp,id++);
                }else{
                    //open表有该项
                    int gscore = GScore[Curid] + 1,fscore = evalute(tmp,target) + gscore;
                    if(fscore < FScore[state]){
                        path[state] = Curid;
                        GScore[state] = gscore;
                        FScore[state] = fscore;
                        openCloseList[state] = false;
                    }
                }
            }
        }
        //当前节点添加到close表中
        openCloseList[Curid] = true;

        //找到open表中fscore最小的做为下一个带搜索节点
        int minCur = -1;
        for(int i = 0;i < id;i ++)
            if(!openCloseList[i] && (minCur == -1 || FScore[i] < FScore[minCur])) minCur = i;
        Curid = minCur;
        getState(stateSpace,curState,Curid);
        if(id == maxState) return -1;
    }
    return Curid;
}

void show(int stateSpace[N][N][maxState],int n)
{
    cout << "-------------------------------\n";
    for(int i = 0;i < N;i ++){
        for(int j =0;j < N;j ++){
            cout << stateSpace[i][j][n] << " ";
        }
        cout << endl;
    }
    cout << "-------------------------------\n";
}

int calDe(int stateSpace[N][N])
{
    int sum = 0;
    for(int i = 0;i < N*N;i ++){
        for(int j = i+1;j < N*N;j ++){
            int m,n,c,d;
            m = i/N;n = i%N;
            c = j/N;d = j%N;
            if(stateSpace[c][d] == 0) continue;
            if(stateSpace[m][n] > stateSpace[c][d]) sum ++;
        }
    }
    return sum;
}

//由stateA通过随机移动自动生成新状态
void autoGenerate(int stateA[N][N])
{
    int maxMove = 50;
    srand((unsigned)time(NULL));
    int tmp[N][N];
    while(maxMove --){
        int dir = rand()%4 + 1;
        if(move(stateA,tmp,dir)) statecpy(stateA,tmp);
    }
}

int main()
{
    //1 定义状态空间
    int stateSpace[N][N][maxState] = {{{0}}};
    //2 初始化起点和终点
    int start[N][N] = {{1,2,3},{4,5,6},{7,8,0}};
    autoGenerate(start);
    int target[N][N] = {{1,2,3},{4,5,6},{7,8,0}};
    //3 检查一致性
    if(!(calDe(start)%2 == calDe(target)%2)){
        cout << "无解\n";
        return 0;
    }
    //4 A*寻路
    int path[maxState] = {0};
    int res =  Astar(stateSpace,start,target,path);
    if(res == -1){
        cout << "达到最大搜索能力\n";
        return 0;
    }
    //5 重构路径
    int shortest[maxState] = {0},j = 0;
    while(res != 0){
        shortest[j++] = res;
        res = path[res];
    }
    //6 显示路径
    cout << "第 0 步\n";
    show(stateSpace,0);
    for(int i = j - 1;i >= 0;i --){
        cout << "第 " << j-i << " 步\n";
        show(stateSpace,shortest[i]);
    }
    return 0;
}

5.2 优化后的代码

#include <iostream>
#include <queue>
#include <vector>
#include <ctime>
#include <cstdlib>
#include <functional>
#include <unordered_map>

#define BoardSize 3
#define DDirectionCount 4
#define InvalidKey 0

int directions[DDirectionCount][2] ={
    {-1,0},{1,0},
    {0,-1},{0,1}
};

struct hashNode
{
    uint64_t m_key;   //散列值
    int m_FScore;//Final Score 总成本
    int m_HScore;//Heuristic Score 启发式分数
    int m_GScore;//Goal Score 消耗的实际分数
    uint64_t m_ParentKey; // 父节点的键值
    hashNode(uint64_t key, int FScore, int HScore, int GScore, uint64_t parentKey)
        : m_key(key), m_FScore(FScore)
        , m_HScore(HScore), m_GScore(GScore) , m_ParentKey(parentKey){}
};

namespace std {
template<>
struct hash<hashNode> {
    size_t operator()(const hashNode& node) const {
        return node.m_key;
    }
};
}

//计算启发估计值
int calHeuristicScore(uint64_t stateKey,uint64_t targetKey)
{
    //对应点位值不一致，启发估计值便加一
    int num = 0;
    uint64_t mask = 0b1111;
    for(int posId = 0;posId < BoardSize*BoardSize; ++ posId){
        if((stateKey & (mask << posId*4)) != (targetKey & (mask << posId*4))) ++ num;
    }
    return num;
}

//计算状态散列值，将二维数据按行展开，再以二进制码拼接成整数
uint64_t stateToHash(int state[BoardSize][BoardSize]){
    uint64_t key = 0;
    uint64_t shift = 0;
    for(int row = 0; row < BoardSize; ++row){
        for(int col = 0; col < BoardSize; ++col){
            key |= ((uint64_t)state[row][col] << shift);
            shift += 4;
        }
    }
    return key;
}

//由状态散列值反推状态
void hashToState(int state[BoardSize][BoardSize], uint64_t key){
    uint64_t shift = 0;
    int mask = 0b1111;

    for(int row = 0; row < BoardSize; ++row){
        for(int col = 0; col < BoardSize; ++col){
            // 从key中提取出4位，并赋值给state[row][col]
            state[row][col] = (key >> shift) & mask;
            shift += 4;
        }
    }
}

//状态转换
int posIdToPostion[9][2] = {
    {0,0},{0,1},{0,2},
    {1,0},{1,1},{1,2},
    {2,0},{2,1},{2,2}
};

uint64_t stateMove(uint64_t key, int dir)
{
    //获取空位
    int posID = 0;
    uint64_t mask = 0b1111;
    for(; ((key&mask<<(posID*4)) >> (posID*4)) != 0 && posID < BoardSize*BoardSize; ++posID);
    //获取移动后坐标以及ID
    int newRow, newCol;
    newRow = posIdToPostion[posID][0] + directions[dir][0];
    newCol = posIdToPostion[posID][1] + directions[dir][1];
    if(newRow < 0 || newRow >= BoardSize || newCol < 0 || newCol >= BoardSize) return InvalidKey;
    int newPosID = newRow * BoardSize + newCol;
    //求新的散列值
    uint64_t newState = key;
    // 设置新位置
    newState &= ~(mask << (newPosID * 4));
    // 设置旧位置
    uint64_t num = ((key&mask<<(newPosID*4)) >> (newPosID*4));
    newState |= num << (posID*4);
    return newState;
}

int AStar(int start[BoardSize][BoardSize],int target[BoardSize][BoardSize],std::vector<uint64_t> &path)
{
    //定义open表和close表
    std::unordered_map<uint64_t, hashNode> openList;
    std::unordered_map<uint64_t, hashNode> closeList;

    uint64_t startKey = stateToHash(start);
    uint64_t targetKey = stateToHash(target);


    //初始化open表
    uint64_t curKey = startKey;

    int hScore = calHeuristicScore(startKey, targetKey);
    int gScore = 0;
    int fScore = hScore + gScore;

    openList[curKey] = hashNode(curKey, fScore, hScore, gScore, curKey);


    // 使用优先队列来存储待探索的节点，按照F分数排序
    auto comp = [&openList](const uint64_t& a, const uint64_t& b) {
        return openList[a].m_FScore > openList[b].m_FScore;
    };
    std::priority_queue<uint64_t, std::vector<uint64_t>, decltype(comp)> openPQ(comp);
    openPQ.push(curKey);

    while(!openPQ.empty() && curKey != targetKey){
        //open表不为空 && 未找到目标节点
        curKey = openPQ.top();
        openPQ.pop();

        for(int direciton = 0; direciton < DDirectionCount; ++ direciton){
            uint64_t newState = stateMove(curKey, direciton);
            //状态是合法且不在close表中
            if(newState != InvalidKey && closeList.find(newState) == closeList.end()){
                auto iter = openList.find(newState);
                //更新当前状态分数
                hScore = calHeuristicScore(newState, targetKey);
                gScore = openList[curKey].m_GScore + 1;
                fScore = hScore + gScore;
                if(iter == openList.end() || fScore < openList[newState].m_FScore){
                    //更新规: 1 不在open表中 || 2 比open表中的值更优
                    openList[newState] = hashNode(newState, fScore, hScore, gScore, curKey);
                    openPQ.push(newState);
                }
            }
        }
        //将当前节点移入closeList
        closeList[curKey] = openList[curKey];

        //将当前节点移除openList
        openList.erase(curKey);

    }
    //重构路径
    uint64_t cur = targetKey;
    while (cur != startKey) {
        path.push_back(cur);
        cur = closeList[cur].m_ParentKey; // 回溯父节点
    }
    path.push_back(startKey);
    std::reverse(path.begin(), path.end()); // 反转路径以从起点开始
    return 0;
}

int calDe(int state[BoardSize][BoardSize])
{
    int sum = 0;
    for(int i = 0;i < BoardSize*BoardSize;i ++){
        for(int j = i+1;j < BoardSize*BoardSize;j ++){
            int m,n,c,d;
            m = i/BoardSize;n = i%BoardSize;
            c = j/BoardSize;d = j%BoardSize;
            if(state[c][d] == 0) continue;
            if(state[m][n] > state[c][d]) sum ++;
        }
    }
    return sum;
}

void show(uint64_t key,int id = -1)
{
    std::cout << "------------No." << id << " Move-------------------\n";
    uint64_t mask = 0b1111;
    for(int posID = 0;posID < BoardSize*BoardSize; ++posID){
        if(posID % BoardSize == 0) std::cout << std::endl;

        std::cout << uint64_t(((key & (mask << (posID*4))) >> (posID*4))) << " ";
    }
    std::cout << std::endl;
    std::cout << "-------------------------------\n";
}

void autoGenerate(int state[BoardSize][BoardSize])
{
    int maxMove = 50;
    srand((unsigned)time(NULL));
    uint64_t curKey = stateToHash(state);
    while(maxMove --){
        int dir = rand()%DDirectionCount;
        uint64_t tmpKey = stateMove(curKey,dir);
        if(tmpKey != InvalidKey) curKey = tmpKey;
    }
    hashToState(state, curKey);
}



int main()
{
    int start[BoardSize][BoardSize] = {{1,2,3},{4,5,6},{7,8,0}};
    int target[BoardSize][BoardSize] = {{1,2,3},{4,5,6},{7,8,0}};

    autoGenerate(target);


    if(!(calDe(start)%2 == calDe(target)%2)){
        std::cout << "no solve\n";
        return 0;
    }

    std::vector<uint64_t> path;
    AStar(start,target,path);

    for(uint16_t id = 0;id < path.size(); ++id) show(path[id], id);

    return 0;
}