1.堆的基本概念:
严格来讲,堆有不同的种类,但是我们在算法学习中,主要用的还是二叉堆,而二叉堆有最大堆和最小堆之分。
最大(最小)堆是一棵每一个节点的键值都不小于(大于)其孩子(如果存在)的键值的树。大顶堆是一棵完全二叉树,同时也是一棵最大树。小顶堆是一棵完全完全二叉树,同时也是一棵最小树。
需要注意的问题是:堆中的任一子树也还是堆,即大顶堆的子树也都是大顶堆,小顶堆同样。
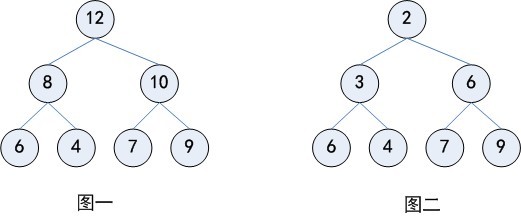
如图一为大顶堆,图二为小顶堆(摘自CSDN博客)
2.堆的一些基本性质:
首先我们从上图中可以看出,由于堆是一棵完全二叉树,那么我们可以得出堆的如下性质:
(1). 堆的插入和删除操作,运行时间为 O(logn),n 为树上结点的个数
简单证明:
假设该二叉树总共有x层,那么很明显当该二叉树为满二叉树的时候,插入和删除耗费的时间是最长的,那么则有:
2^x - 1 = n;
在最坏的情况下,我们插入一个元素的时候,是从第一层遍历到第n层(反之也一样),那么我们最多要进行的操作次数即为树的深度,而树的深度x = log(2)(n+1)(表示以2为底,以n+1为真数的对数),忽略常数,那么我们就求得插入时的最坏时间复杂度则为O(logn)级别。
删除与插入同理,删除时需要注意的问题就是,删除一个元素之后,需要重新调整堆的结构,使其成为新的堆。
(2).堆可以看成是一棵完全二叉树,除最后一层其余每层结点都是满的。
3.堆的插入和删除操作实现:
(1).首先我们看堆的插入操作:
图转自http://blog.csdn.net/cdnight/article/details/11650983/
如上图所示,是一个大根堆的插入演示,插入的数据元素为80,一开始的时候,我们将待插入的数据元素接至堆的末尾,然后再不断向上提升直至没有大小颠倒为止。
我们以上图为例简述堆插入元素的过程:
一开始的时候,元素80和其父亲节点比较,发现其大于父亲节点,因此要上溢,将元素80与其父亲节点进行交换,交换后再重复上述过程,发现元素80仍然比其父亲节点大,继续上溢,将元素80与其父亲节点进行交换,然后再将其与父亲节点比较,发现此时小于其父亲节点的值,说明此时堆中不再存在大小颠倒了,那么此时元素80找到了它在堆中的位置,插入操作结束。
在实现以上算法分析过程时,我们需要明确的问题是,我们不使用指针来表示二叉树,而是用数组存储(因为在这里的堆是完全二叉树的原因,因此用数组实现更简单,而且不存在大量的空间浪费),所以呢,对于每个节点,如果其有左孩子和右孩子的话,那么:
(1).左孩子节点的编号是其自身节点编号 * 2 + 1;
(1).右孩子节点的编号是其自身节点编号 * 2 + 2;(编号是指其用数组中存储时的下标)
因此根据上述分析,得出代码:
//往堆中插入元素,数组下标从0开始
void push(int value){ //value表示插入堆的值
Heap[size] = value; //一开始元素接在堆的最后面
int current = size; //表示当前遍历到的节点
int father = (current-1) / 2; //表示当前遍历到的堆中元素父亲节点的下标
while(current > 0 && Heap[current] < Heap[father]){
swap(Heap[current],Heap[father]); //表示此时节点"上溢",当前节点与其父节点对换.
current = father;
father = (current-1) / 2; //继续向上遍历
}
++size;
}在删除操作中,我们这里介绍一下简单的删除堆顶元素,在删除堆顶元素之前,那么我们首先要明白的是要如何获取堆顶元素:
很容易想到,堆顶元素自然是数组 data 存储的第 0 位元素。
因此我们可以想到用如下代码获取堆顶元素:
//获取堆顶元素
int top(){
return Heap[0];
}所以这里我们这样删除堆顶元素:将堆顶元素和堆的最后一个元素进行交换,然后对堆顶元素做一个自上而下的堆调整,也就是下滤操作。
下滤操作和上溢操作类似,也是不断交换父亲节点以及其孩子节点,然后更新当前遍历到的节点的编号以及其孩子节点的编号,直到堆中没有大小颠倒为止。
那么根据以上分析,我们可以得出以下完整代码:
/**删除栈顶元素
*删除栈顶元素时,不可直接将size的值减一后就结束,这样的话会破坏整个
*二叉堆的结构,因此我们在删除堆顶元素之后还要调整堆的结构,使其成为新的堆
*并且有新的堆顶元素
*/
void pop(){
Heap[0] = Heap[--size]; /*首先将最后一个元素替换堆顶元素,这样的话堆顶元素则被删除
*然后再是size减一表示堆中元素数目减一
*/
int current = 0; //当前遍历到的节点的下标
int lchild = current*2 + 1,rchild = current*2 + 2; //当前遍历到的节点的左孩子和右孩子节点的下标
while(lchild < size && min(Heap[lchild],Heap[rchild]) < Heap[current]){
if(Heap[lchild] < Heap[rchild]){
swap(Heap[lchild],Heap[current]);
current = lchild; //"下溢"的过程
}
else{
swap(Heap[rchild],Heap[current]);
current = rchild;
}
lchild = current*2 + 1;
rchild = current*2 + 2;
}
}需要特别注意的问题是,这种情况对于删除堆顶元素适用,但是要删除堆中的其他元素,下溢法会出错。详细分析:
【算法】堆,最大堆(大顶堆)及最小堆(小顶堆)的实现【2】---软件截图及算法代码
整个二叉堆(小根堆)插入和删除操作的完整实现代码:
//二叉堆(数组存储)的插入,删除堆顶元素(以小根堆为例,即堆顶元素最小)
#include<cstdio>
#include<algorithm>
using namespace std;
const int Max_size = (int)1e3; //表示堆中能够容纳元素个数的最大值
int size = 0,Heap[Max_size]; //记录当前堆中元素下标最大值
//往堆中插入元素,数组下标从0开始
void push(int value){ //value表示插入堆的值
Heap[size] = value; //一开始元素接在堆的最后面
int current = size; //表示当前遍历到的节点
int father = (current-1) / 2; //表示当前遍历到的堆中元素父亲节点的下标
while(current > 0 && Heap[current] < Heap[father]){
swap(Heap[current],Heap[father]); //表示此时节点"上溢",当前节点与其父节点对换.
current = father;
father = (current-1) / 2; //继续向上遍历
}
++size;
}
/**删除栈顶元素
*删除栈顶元素时,不可直接将size的值减一后就结束,这样的话会破坏整个
*二叉堆的结构,因此我们在删除堆顶元素之后还要调整堆的结构,使其成为新的堆
*并且有新的堆顶元素
*/
void pop(){
Heap[0] = Heap[--size]; /*首先将最后一个元素替换堆顶元素,这样的话堆顶元素则被删除
*然后再是size减一表示堆中元素数目减一
*/
int current = 0; //当前遍历到的节点的下标
int lchild = current*2 + 1,rchild = current*2 + 2; //当前遍历到的节点的左孩子和右孩子节点的下标
while(lchild < size && min(Heap[lchild],Heap[rchild]) < Heap[current]){
if(Heap[lchild] < Heap[rchild]){
swap(Heap[lchild],Heap[current]);
current = lchild; //"下溢"的过程
}
else{
swap(Heap[rchild],Heap[current]);
current = rchild;
}
lchild = current*2 + 1;
rchild = current*2 + 2;
}
}
//获取堆顶元素
int top(){
return Heap[0];
}
//输出堆中元素
void output(){
for(int i = 0;i < size;++i){
printf("%d ",Heap[i]);
}
printf("\n");
}
int main(){
int a[6];
for(int i = 0;i < 6;++i){
scanf("%d",&a[i]);
push(a[i]);
}
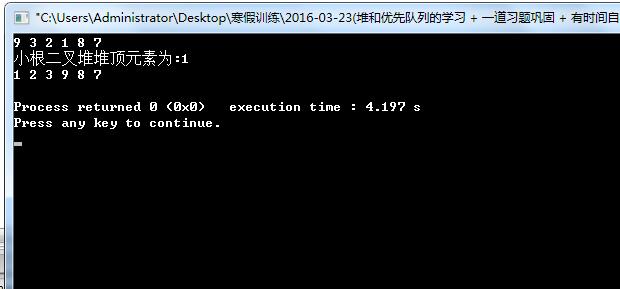
printf("小根二叉堆堆顶元素为:%d\n",top());
output();
return 0;
}
运行效果实现:
C++实现的大根堆的插入和删除操作:
#include<iostream>
using namespace std;
class Heap {
private:
int *data, size;
public:
Heap(int length_input) {
data = new int[length_input];
size = 0;
}
~Heap() {
delete[] data;
}
void push(int value) {
data[size] = value;
int current = size;
int father = (current - 1) / 2;
while (data[current] > data[father]) {
swap(data[current], data[father]);
current = father;
father = (current - 1) / 2;
}
size++;
}
void output() {
for (int i = 0; i < size; i++) {
cout << data[i] << " ";
}
cout << endl;
}
int top(){
return data[0];
}
void update(int pos,int n){
int lchild = 2 * pos + 1,rchild = 2 * pos + 2;
int max_value = pos;
if(lchild < n && data[lchild] > data[max_value]){
max_value = lchild;
}
if(rchild < n && data[rchild] > data[max_value]){
max_value = rchild;
}
if(max_value != pos){
swap(data[pos],data[max_value]);
update(max_value,n);
}
}
void pop(){
swap(data[0],data[size-1]);
--size;
update(0,size);
}
};
int main() {
int arr[10] = { 12, 9, 30, 24, 30, 4, 55, 64, 22, 37 };
Heap heap(100);
for (int i = 0; i < 10; i++) {
heap.push(arr[i]);
}
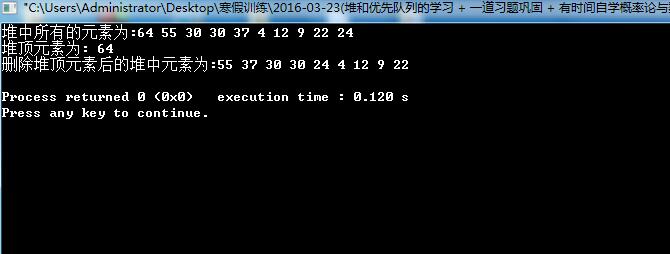
cout << "堆中所有的元素为:";
heap.output();
cout <<"堆顶元素为: " << heap.top() << endl;
heap.pop(); //删除堆顶元素
cout << "删除堆顶元素后的堆中元素为:";
heap.output();
return 0;
}
总结:堆和优先队列是非常常用和重要的数据结构,不管是手写还是用STL实现,都要熟练掌握。
如有错误,还请指正,O(∩_∩)O谢谢




























 1504
1504

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








