A题:
题目描述:
The Water Problem
In Land waterless, water is a very limited resource. People always fight for the biggest source of water. Given a sequence of water sources with a1,a2,...,an representing the size of the water source. Given a set of queries each containing 2 integers l and r, please find out the biggest water source between al and ar.
First you are given an integer T (T <= 10) indicating the number of test cases. For each test case, there is a number n (0 <= n <= 1000) on a line representing the number of water sources.n integers follow, respectively a1,a2,...,an, and each integer is in {1, . . . , 10^6}. On the next line, there is a number q (0 <= q <= 1000) representing the number of queries. After that, there will be q lines with two integers l and r (1 <= l <= r <= n) indicating the range of which you should find out the biggest water source.
3 1 100 1 1 1 5 1 2 3 4 5 5 1 2 1 3 2 4 3 4 3 5 3 1 999999 1 4 1 1 1 2 2 3 3 3
100 2 3 4 4 5 1 999999 999999 1
给定T组测试数据,每组测试数据的第一行数是n,表示有n个数字,接下来的一行为n个数字,然后再接下来的一行是一个数q,表
示有q组询问,每组询问占一行,有两个数l,r,然后对于每一组询问输出在第l个到第r个数中(包含边界)最大的数。
解析:
由于n和q的范围都不大,均小于1000,因此暴力求解即可。时间复杂度为O(n*q),注意当数据范围较大的时候,可用线段树求解,
总体的时间复杂度为O(q * logn).
完整代码实现:
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAX_N = (int)1e3 + 10;
int a[MAX_N];
int main(){
int T,n,q,x,y;
scanf("%d",&T);
while(T--){
scanf("%d",&n);
for(int i = 1;i <= n;++i){
scanf("%d",&a[i]);
}
scanf("%d",&q);
while(q--){
scanf("%d %d",&x,&y);
int ans = 0;
for(int i = x;i <= y;++i){
ans = max(a[i],ans);
}
printf("%d\n",ans);
}
}
return 0;
}
题目描述:
T^T找数字
有一天,T^T来到了师大比赛,看上了师大的ACMer小彩,于是他就跑上去想跟人家搭讪,可是呢,这时候,小彩遇到了一个问题,小彩说,你要是帮我解决了这个
问题,我就把我的手机号给你,T^T一听,顿时乐了起来,这不是我的强项嘛,于是就让小彩说了:
给定整数a1,a2,....,an,判断是否可以从中选出若干数(取数的数目 > 0),使它们的和恰好为k
输入有多组数据,输入的第一行有两个数,分别为n,k(1 <= n <= 20,-10^8 <= k <= 10^8,不考虑k = 0的情况);
第二行是n个数,分别是a1,a2,a3,...,an(-10^8 <= ai <= 10^8)
能找到这样的若干个数的和为k(由于oj无法特判,因此输入保证只有一组这样的数),则输出YES,并且按照顺序输出这些数,否则的话,输出NO
4 13 1 2 4 7 4 15 1 2 4 7
YES 2 4 7 NO
B题是我从《挑战程序设计竞赛》》上看到的题目,并对其进行了简单的改编。因此也就没有放入比较强的测试数据(其实是我
懒O(∩_∩)O),只是让大家感受一下入门的搜索算法。
废话少说,题目是说要从给定的n个数中,是否能够找出若干个数(注意这若干个数显然是可以不连续的),使得这些数的和为
k,若能,则输出YES,并且按顺序输出这些数;若不能,则输出NO。
我们用一个临时变量sum来标记这些数的和,显然,一开始的时候,sum的值为0.然后我们考虑给定的这n个数,对于每个
数,只有两种状态,要么取这个数,要么不取,而这道题n的数据范围是n<=20,因此我们可以考虑遍历所有的状态,而将这些状态
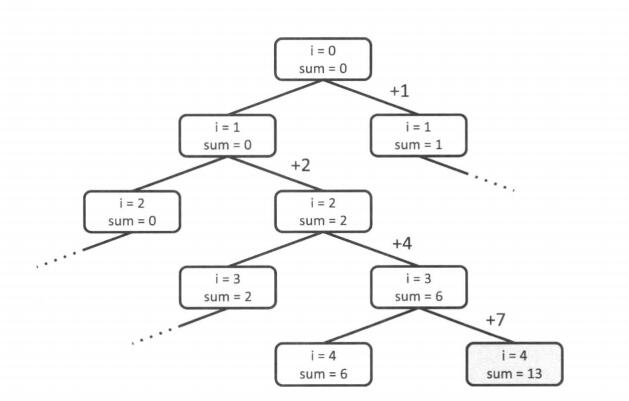
用图形描述出来则是下图:
从上图我们可知,所有状态组成了一棵满二叉树,因此我们可以对这棵满二叉树进行先序遍历,穷竭遍历所有的状态,当匹配到
sum == k时,那么从这个节点开始返回根节点,由于要顺序输出组成k的这若干个数,因此我们可以用栈存储这些数,在我们在匹配
到sum == k时,由于我们要沿着根节点的路径返回,直至返回整棵树的根节点,因此我们可以在返回的路径中,将途经的数据元
素压入栈中。直至返回到整棵树的根节点时,将栈中元素一一输出即可。
当然,这道题也可以进行一些剪枝操作,比如说此时遍历到的节点sum值已经大于k时,那么该节点的孩子节点则不必再遍
历。因此可以不必每次都遍历到叶节点再回溯,这样的话省去了不必要的遍历操作。
完整代码实现:
#include<cstdio>
#include<cstring>
#include<stack>
using namespace std;
const int MAX_N = 25;
int n,k,flag,num[MAX_N];
stack <int> s;
//i表示当前考虑到了哪个数,sum表示当前和
bool dfs(int i,int sum){
if(sum > k){
return false; //剪枝操作
}
//如果前n项均已经计算过,那么判断此时sum的值是否与k相等,并回溯至上一层
if(i==n){
return k==sum;
}
//加上a[i]的情况
if(dfs(i+1,sum+num[i])){
s.push(num[i]);
return true;
}
//不加上a[i]的情况
if(dfs(i+1,sum)){
return true;
}
return false;
}
int main(){
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
while(scanf("%d %d",&n,&k)!=EOF){
memset(num,0,sizeof(num));
for(int i = 0;i < n;++i){
scanf("%d",&num[i]);
}
if(dfs(0,0)){
printf("YES\n");
while(!s.empty()){
printf("%d ",s.top());
s.pop();
}
printf("\n");
}
else{
printf("NO\n");
}
}
return 0;
}
C题:
题目描述:
T^T又有数学问题了
T^T 是个很厉害的选手,除了喜欢写17kb+的代码题,偶尔还会写数学题.他找到了一个数列:

他给了你几个数:n,a,b,c,你需要告诉他fn模p后的数值.
第一行一个数T,为测试数据组数.
每组数据一行,一行五个正整数,按顺序为n,a,b,c,p.
1≤T≤10,1≤n≤10^18,1≤a,b,c≤10^9,p是质数且p≤10^9+7
对每组数据输出一行一个数,输出fn对p取模后的数值.
1 5 3 3 3 233
190
这道题没有完整代码提供,因为这道题还有没有弄明白的地方,而且雏形代码一直没调试好:-(,这里提供简要思路
对于这样的题目,一开始拿到手的时候没有什么明朗的思路,因此我们可以试着枚举前几项,看看是否从特殊的角度发现其一般规
律。
f1 = 1;
f2 = a^b;
f3 = a^b * a^(bc) * 1 = a^[b(1+c)];
f4 = a^b * f3^c * f2 = a^[b(c^2 + c + 2)];
f5 = a^b * f4^c * f3 = a^[b(c^3 + c^2 + 3*c + 2)];
f6 = a^b * f5^c * f4 = a^[b(c^4 + c^3 + 4 * c ^ 2 + 3*c + 3)];
枚举到第六项,我们发现,每一项都有其相同的部分,因此我们可以去掉相同的部分,看剩余不同的部分是否有规律:
0 ---------> f1
1 ---------> f2
1+c ---------> f3
c^2 + c + 2 ---------> f4
c^3 + c^2 + 3*c + 2 ---------> f5
c^4 + c^3 + 4 * c ^ 2 + 3*c + 3 ---------> f6
仔细观察,其实不难发现,每一项(第三项及第三项之后)都与其前两项是有联系的。比如说f3,f4,f5.我们可以找到它们之间的这样
的关系:
f3 + f4 * c + 1 = f5;
而有了这样的推论之后,我们可以发现:f(n) = c * f(n-1) + f(n-2) + 1;
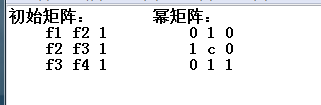
而多项式之间的关系,则可以借助于矩阵来解决,对于有常数项的多项式,则用三维矩阵即可(常数视为第三维)。
因此有了以上的推论,我们可以构造出这样的初始矩阵以及幂矩阵:
因此我们则可以将初始矩阵记为A矩阵,幂矩阵记为B矩阵,这样的话,要求fn,则即求A * B ^ (n-1),然后取结果矩阵的首项即可。
而要求A * B ^ (n-1),则可用矩阵快速幂求解。
但是,这道题还有两个要注意的小细节:
1.B ^ (n-1)指数过大,long long已经无法存储,我个人有个想法:
(1).对等式两边运用log函数,以a为底,这样的话,就把幂指数降下来了。
(2).第二个办法是从福州大学陈鸿数论pdf文档中看到了一个结论:
这个结论我暂时没有办法解释,涉及到欧拉函数和费马小定理,证明过程在这里,有兴趣的可以一起研究探讨:
2.注意特判a与p不互质(a mod p = 0)的情况。
E题:
题目描述:
Complicated GCD
Greatest common divisor GCD(a, b) of two positive integers a and b is equal to the biggest integer d such that both integers a and b are divisible by d. There are many efficient algorithms to find greatest common divisor GCD(a, b), for example, Euclid algorithm.
Formally, find the biggest integer d, such that all integers a, a + 1, a + 2, ..., b are divisible by d. To make the problem even more complicated we allow a and b to be up to googol, 10100 — such number do not fit even in 64-bit integer type!
The only line of the input contains two integers a and b (1 ≤ a ≤ b ≤ 10100).
Output one integer — greatest common divisor of all integers from a to b inclusive.
1 2
1
61803398874989484820458683436563811772030917980576 61803398874989484820458683436563811772030917980576
61803398874989484820458683436563811772030917980576
给定a,b,找出能够整除闭区间[a,b]中所有的数的最大整数。
解析:
简单题,考虑当a == b时,显然这个数就是其本身,而当a != b时,由于连续的两个正整数的公共因子只有1(可用反证法证明),因此
答案则是1.
完整代码实现:
#include<string>
#include<iostream>
using namespace std;
int main(){
string a,b;
cin >> a >> b;
if(a==b){
cout << a << endl;
}
else{
cout << 1 << endl;
}
return 0;
}F题:
题目描述:
Solve equation
You are given two positive integers A and B in Base C. For the equation:
We know there always existing many non-negative pairs (k, d) that satisfy the equation above. Now in this problem, we want to maximize k.
For example, A="123" and B="100", C=10. So both A and B are in Base 10. Then we have:
(1) A=0*B+123
(2) A=1*B+23
As we want to maximize k, we finally get one solution: (1, 23)
The range of C is between 2 and 16, and we use 'a', 'b', 'c', 'd', 'e', 'f' to represent 10, 11, 12, 13, 14, 15, respectively.
The first line of the input contains an integer T (T≤10), indicating the number of test cases.
Then T cases, for any case, only 3 positive integers A, B and C (2≤C≤16) in a single line. You can assume that in Base 10, both A and B is less than 2^31.
3 2bc 33f 16 123 100 10 1 1 2
(0,700) (1,23) (1,0)
给定一个数T,表示有T组测试数据,然后每行有三个数,分别是A,B,C。C表示给定的A,B数的进制,然后题目要求你将A,B转换成十
进制后,找出一个最大的数k,使得k,d满足A = k * B + d(其中k,d均为非负整数)。
解析:
显然我们要将其转换成十进制数之后,然后按照格式输出即可。注意这道题不要去用pow()函数从后往前计算A,B两数十进制所表示
的数,会判CE或者WA,原因未知。无论如何,涉及到浮点数的函数,还是要慎用,能不用则不用。
因此我们从前往后考虑即可,每往后计算一位,则标记数乘以相应进制即可。
完整代码实现:
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
void solve(){
int T,radix,tmp;
char str1[50],str2[50];
scanf("%d",&T);
while(T--){
scanf("%s %s %d",str1,str2,&radix);
int a = 0,b = 0;
for(int i = 0;str1[i] != '\0';++i){
a *= radix;
if(str1[i] >= 'a'){
a += str1[i] - 'a' + 10;
}
else{
a += str1[i] - '0';
}
}
for(int i = 0;str2[i] != '\0';++i){
b *= radix;
if(str2[i] >= 'a'){
b += str2[i] - 'a' + 10;
}
else{
b += str2[i] - '0';
}
}
//printf("%d %d",a,b);
printf("(%d,%d)\n",a/b,a%b);
}
}
int main(){
solve();
return 0;
}
总结:不要过度依赖库函数,编码能力还是不强,要多锻炼,而且以后题目尽量要自己慢慢弄懂,这样才会是自己的东西。








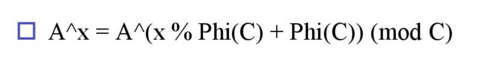














 703
703

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








