[牛客复盘] round11 20230911
总结
- 美团校招原题,但是D好难。
- T1 数学
- T2 枚举
- T3 递推/dp,这题和round9一样,不写了
- T4 二维dp求方案数+剪枝

小美的外卖订单编号
链接: [小美的外卖订单编号
2. 思路分析
- 和round9一样。
3. 代码实现
def solve():
m, x = RI()
x = (x - 1) % m
print(x + 1)
小美的数组操作2
链接: 小美的数组操作2
1. 题目描述

2. 思路分析
- 由于数据范围是100,因此直接暴力即可,也就平方复杂度。
3. 代码实现
def solve():
n, k = RI()
a = RILST()
for _ in range(k):
u,v = RI()
a[u-1] += 1
a[v-1] -= 1
for i in range(n-1):
if a[i] > a[i+1]:
return print('No')
print('Yes')
小美的元素删除
链接: 小美的元素删除
1. 题目描述
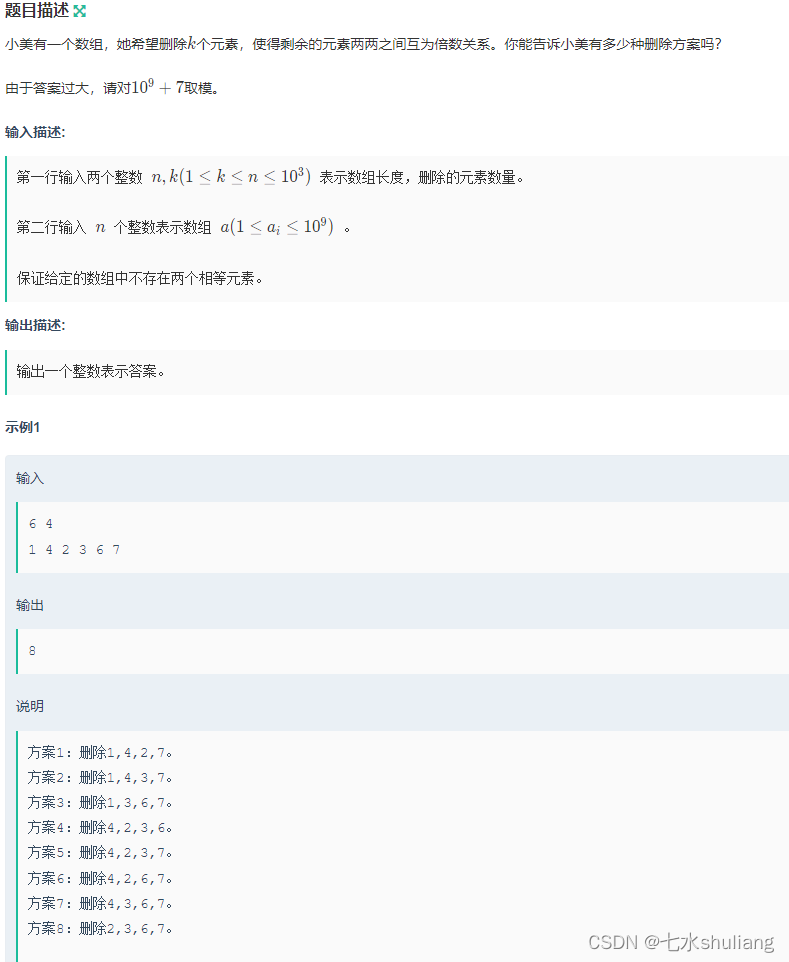
2. 思路分析
- 删除k个不好考虑,反过来考虑保留p=n-k个的方案数。
- 发现合法方案最多保留30个数字。
3. 代码实现
MOD = 10 ** 9 + 7
PROBLEM = """读完题觉得最后保留的数列是一个顺序递增的倍数串,即后一个一定包含前边的因数,那么在1e9内,最长也就只能是全2,长度30。
然后硬写个二维dp,由于是求方案数,因此定义f[i][j]时,表示以i为结尾的方案数,一定要包含i。
那么是可以遍历更小的数,找因数来转移的,由于还要遍历每个长度,因此是三次方。
注意到长度一定<=30,否则就是0,所以可以剪掉这部分。优化成n^2 * 30。
注意到转移时长度只用到前边一个状态,因此状态反过来定义,就可以滚动了。
滚动时可以按背包逆序,只需要一个数组,但是注意这题是求方案数,记得清空
"""
# ms
def solve():
n, k = RI()
a = RILST()
if k == n:
return print(1)
p = n - k
if p > 31: # 不写这个就是n^3,注意到保留的长度最多是30,即2^30约1e9
return print(0)
p = min(p, 31)
a.sort()
f = [1] * n # f[j][i] 以i为结尾,长为j的序列的方案数
for k in range(p - 1):
for i in range(n - 1, -1, -1):
f[i] = 0 # 逆序更新,就可以用一个数组滚动,但是这题求方案数,注意记得清空f[i]
for j in range(i):
if a[i] % a[j] == 0: # 从可行的地方转移来
f[i] += f[j] # 从k-1长度的方案加上a[i],变成尾巴为a[i]长度为k的方案数
f[i] %= MOD
print(sum(f) % MOD)
# ms
def solve2():
n, k = RI()
a = RILST()
if k == n:
return print(1)
p = n - k
if p > 31: # 不写这个就是n^3
return print(0)
p = min(p, 31)
a.sort()
f = [1] * n # f[j][i] 以i为结尾,长为j的序列的方案数
for k in range(p - 1):
g = [0] * n
for i, v in enumerate(a):
for j in range(i):
if v % a[j] == 0: # 从可行的地方转移来
g[i] += f[j] # 从k-1长度的方案加上a[i],变成尾巴为a[i]长度为k的方案数
g[i] %= MOD
f = g
print(sum(f) % MOD)
# ms
def solve1():
n, k = RI()
a = RILST()
if k == n:
return print(1)
p = n - k
if p > 31: # 不写这个就是n^3
return print(0)
p = min(p, 31)
a.sort()
f = [[0] * (p + 1) for _ in range(n)] # f[i][j] 以i为结尾,长为j的序列的方案数
for i in range(n):
f[i][1] = 1
for i, v in enumerate(a):
for j in range(i):
if v % a[j] == 0: # 从可行的地方转移来
for k in range(2, p + 1):
f[i][k] += f[j][k - 1] # 从k-1长度的方案加上a[i],变成尾巴为a[i]长度为k的方案数
f[i][k] %= MOD
ans = 0
for i in range(n):
ans += f[i][p]
ans %= MOD
print(ans)
六、参考链接
- 无








 文章解析了美团校招面试中的三道题目:外卖订单编号的数学问题、数组操作的暴力解法和元素删除的方案计数,涉及T1-T4难度,以及使用了动态规划和枚举等技巧。
文章解析了美团校招面试中的三道题目:外卖订单编号的数学问题、数组操作的暴力解法和元素删除的方案计数,涉及T1-T4难度,以及使用了动态规划和枚举等技巧。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








