bayer AHD插值

最新推荐文章于 2025-04-28 20:40:39 发布

原创最新推荐文章于 2025-04-28 20:40:39 发布

· 2k 阅读

4 ·

版权

算法专栏收录该内容

58 篇文章

订阅专栏

本文介绍了AHD(Auto Homogeneity Directed)插值算法在RAW图像处理中的应用，详细阐述了G、RB的插值步骤，并讨论了算法性能、计算耗时以及可能的优化方向。通过对原始滤波器的分析，提出了对二阶导数相等的假设以及使用中值滤波修正artifact的问题。实验表明，插值公式的选择对最终结果有显著影响，而计算参数的自适应调整至关重要。此外，C代码实现的AHD插值在12M像素的Bayer图像上耗时190ms，主要瓶颈在于step4的比较操作。引用了相关研究文献以深入理解该领域的进展。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最近做RAW，遇到一些issue涉及到raw的伪彩，为了有希望解决这个问题，去看了下AHD paper，希望能学到一些技巧有助于帮助伪彩的解决。这里做个记录。

AHD插值

step1. G的插值： paper里用最优化过程导出了一个filter。

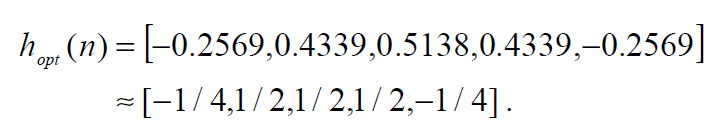
filter 长度为5，对于R0,G1,R2,G3,R4，运用该filter可得到G2的值。

这个定点化后的filter的理解(性质)：

若进行变形可得到 a. G2 = weight（Gi-Ri）+R2，也就是说R2加上一定的值，这个值是附近已知的相邻的4个G-R对的加权平均。

另一种变形可得到 b. $2((G2-G1)-(G3-G2))=((R2-R0)-(R4-R2))$ ,也就是说已知两个G加上待求G配成对的二阶导，与已知的3个R配成的二阶导相等，二阶导相等推出来的filter就是paper中filter。

上面变形一是为了尝试理解，二是希望能利用性质，后续实现AHD算法的时候有希望有快速实现算法。

step 2: RB的插值。这里paper里使用的是step1得到的G，来计算已知半通道的G-R，然后双线性插值出整张图的G-R，然后得到R。

这里考虑上面的变形a, 另d=G-R,则 step12都是使用已知的相邻G-R对来求解d，如果合并step12公式，会发现，求G位置的d时，使用的是4个G-R对以1/4加权平均，而在求R位置的d时使用的是6个G-R对以1/8,1/4,1/8进行加权平均。这里是比较奇怪的地方，只考虑特定GR行的话，其GR分辨率是一样的，但两者插值方式精度却不一样，是为了性能考虑么？同时这里如果以G-R为对象来进行考虑的话，step12看上去是可以合并公式去除一些冗余计算的。

step 3：分别在行方向与列方向进行插值得到两种BGR图resH, rseV

step 4：最终结果的res的每个点值取resH与resV之一，判断依据就是在特定点区域的resH与resV哪个插值出来的区域homo map相似度最大。

step 5：使用中值滤波进行artifact修正。

综上所述，AHD算法就是在bayer上对D=G-R分别进行行与列方向的插值得到两种结果；然后哪个方向上插出来的区域更相似选哪个，每个点都二选一；最后再artifact refine。

问题来了。

1. 看了下算法公式，前面插值公式对最后结果影响有多大？看上去使用的是二阶导相等来插值，但二阶导BGR上会分别相等么？看上去使用左右梯度的比值而不是插值会不会更合理一些？后续可以验证

当然，paper里最后也对一些参数算法模块进行调整，来看结果的影响。结论是，其中影响比较大的是step 4中计算参数的自适应对结果影响很大

2.若使用未定点化的浮点filter，需要归一化，否则效果不对。

3.最近实现了下AHD插值，纯C代码开4线程，对12M的bayer进行demosaicking还是需要190ms的时间，还是很慢的，对于模块耗时分析，耗时最严重的是step4中上下左右共8次比较大小，应该花了有120ms(这块挺疑惑的，为啥这么慢)。

HA:

J. E. Adams and J. F. Hamilton, “Design of practical color filter array interpolation algorithms for digital cameras,” in Proc. SPIE, vol. 3028, 1997, pp. 117–125.

J. F. Hamilton and J. E. Adams, ‘‘Adaptive color plane interpolation in single sensor color electronic camera,’’ U.S. Patent No. 5,629,734 ~1997!.

AHD:

Hirakawa K, Parks TW. Adaptive homogeneity-directed demosaicing algorithm. IEEE Trans Image
Processing 2005;14(3):360-9.
Hirakawa K, Parks TW. Adaptive homogeneity-directed demosaicing algorithm. Proc IEEE Int
Conf Image Processing 2003;3:669-72.

HIGH-QUALITY LINEAR INTERPOLATION FOR DEMOSAICING OF BAYER-PATTERNED COLOR IMAGES

Demosaicking: Color Filter Array Interpolation in Single-Chip Digital Cameras

Demosaicking methods for Bayer color arrays

Multiframe Demosaicing and Super-Resolution of Color Images