SPSS——方差分析（Analysis of Variance, ANOVA）——多因素方差分析(无重复试验双因素)

简介

当遇到两个因素同时影响结果的情况，需要检验是一个因素起作用，还是两个因素都起作用，或者两个因素的影响都不显著

场景

某公司某种茶饮料的调查分析数据

统计了该茶饮料两种不同的包装（新设计的包装和旧的包装）在三个随机的地点的销售金额，分析销售地点和包装方式对销售金额各有怎样的影响

数学模型

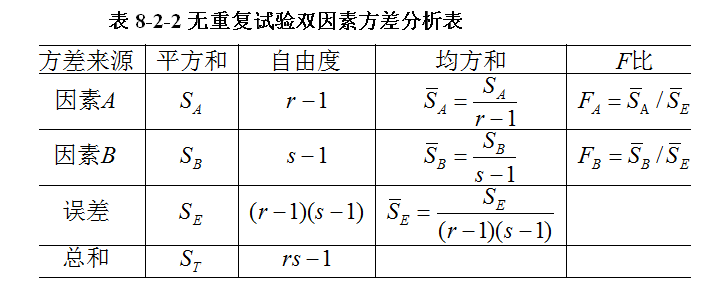
无重复试验双因素的方差分析数学模型

试验区组

假设前提

构建模型

假设检验

偏差平方和及其分解

检验F统计量

方差分析表

菜单

数据源

grocery_1month.sav

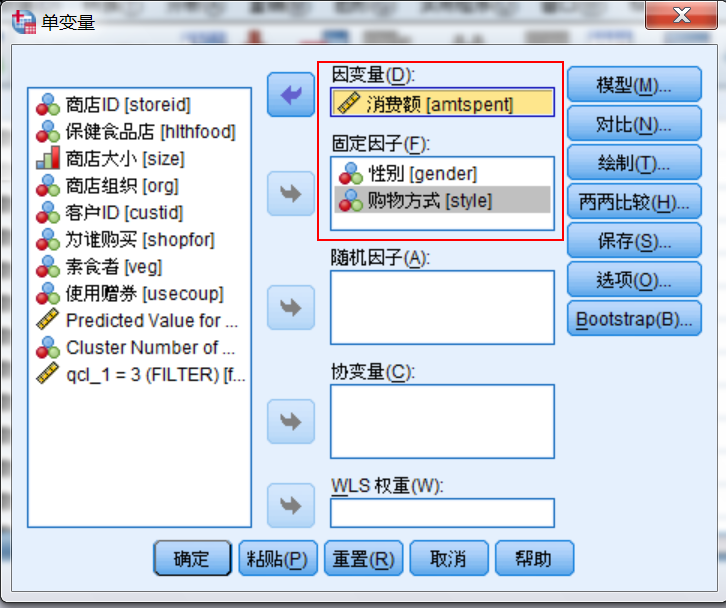
单变量选择

• 因变量
  要进行分析的目标变量，一般为度量变量，数值为数值型。只能选择一个唯一变量。
• 固定因子
  用来分组，一般是可以人为控制的
• 随机因子
  用来分组，各个水平一般是不可以认为控制的，如体重，身高等
• 协变量
  用于协方差分析
  与因变量相关的定量变量，是用来控制其他与因子变量有关且影响方差分析的目标变量的其他干扰因素，类似回归分析中的控制变量
• WLS权重
  选择加权最小二乘法的权重系数
  如果加权变量为0、负数或缺失，则将该个案从分析中排除。已用在模型中的变量不能用于加权变量

模型

• 全因子
  系统默认项，用于建立全模型，分析所有因素的主效应及其交互效应，包括所有因子主效应、所有协变量主效应、所有因子间交互，但不包含协变量交互

• 设定
  表示可以仅指定其中一部分的交互或指定因子协变量交互，必须指定要包含在模型中的所有项

  • 因子与协变量
    列出在Univariate过程中选择的所有的固定因素变量（F）、随机因素变量（R）和协变量（C）
  • 构建项
    交互： 定义进行选择变量的交互效应的方差分析
    主效应：
    定义进行选择变量的主效应的方差分析
    表示模型中仅考虑各个控制变量的主效应而不考虑变量之间的-交互项
    All 2-way - All 5-way：
    定义进行所有变量的i阶交互效应的方差分析
  • 模型
    选择方差分析的主效应。若同时将因子与协变量选项中的两个变量选入，则将其交互效应强行纳入模型

• 平方和
  定义平方和的分解方法
  I 分层平凡和，仅处理主效应
  II 处理所有其他效应
  III 处理I和II中的所有效应
  IV 要考虑所有的二维、三维、四纬的交互效应

• 在模型中包含截距
  如果认为数据回归线可以经过坐标轴原点的话，就可以在模型中不含有截距，但是一般系统默认含有截距项

对比

用于设置比较因素水平间差异的方法

• 无
  不进行因子各水平间的任何比较
• 偏差
  因子变量每个水平与总平均值进行对比
• 简单
  对因子变量各个水平与第一个水平和最后一个水平的均值进行对比
• 差值
  表示对因子变量的各个水平都与前一个水平进行做差比较
• Helmert
  表示对因子变量的各个水平都与后面的水平进行做差比较，当然最后一个水平除外
• 重复
• 多项式
  对每个水平按因子顺序进行趋势分析

绘制

• 水平轴
  均数轮廓图中的横坐标
• 单图
  用来绘制分离线的
• 多图
  每个水平可用来创建分离图

两两比较

参考单因素方差分析，用于确定哪些均值存在差异

保存

• 预测值
  用于保存模型为每个个案预测的值
  
  • 未标准化
    模型为因变量预测的值
  • 加权
    加权未标准化预测值
    仅在已经选择了WLS变量的情况下可用
  • 标准误
    对于自变量具有相同值的个案所对应的因变量均值标准差的估计
• 残差
  用于保存模型的残差
  
  • 未标准化
    因变量的实际值减去由模型预测的值
  • 加权
    在选择了WLS变量时提供加权的未标准化残差
  • 标准化
    对残差进行标准化的值
  • 学生化
    Student化的残差
  • 删除
    表示删除残差
• 诊断
  用于标识自变量的值具有不寻常组合的个案和可能对模型产生很大影响的个案的测量
  
  • Cook距离
    在特定个案从回归系数的计算中排除的情况下，所有个案的残差变化幅度的测量，较大的Cook距离表名从回归统计量的计算中排除个案后，系统会发生根本变化
  • 杠杆值
    未居中的杠杆值，每个观察值对模型拟合的相对影响
• 系数统计
  用于保存模型中的参数估计值的斜方差矩阵

选项

提供一些基于固定效应模型的统计量

• 显示均值
  输出该变量的估算边际均值、标准误等统计量
  比较主效应
  为模型中的任何主效应提供估计边际均值未修正的成对比较
• 输出
• 显著性水平

结果分析

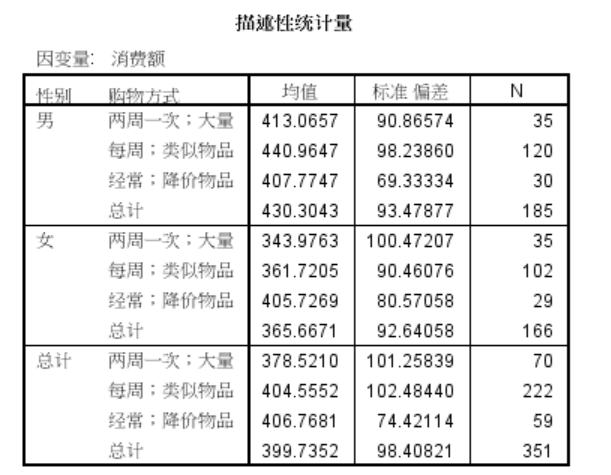
描述性统计量

方差齐性检验

检验的零假设：所有组中因变量的误差方差均相等
可以认为因变量在各个因素水平下的误差方差相等

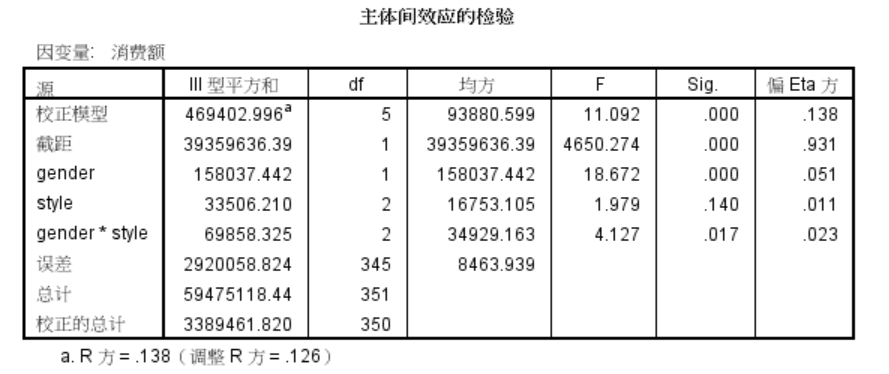
主体间效应的检验

整体模型的Sig < 0.05，此方差模型是显著的
R方 = 0.138，说明消费额的变异被“gender”，“style”，“gender*style”解释的部分有13.8%
gender（性别）对消费额有显著影响