[CSP-J2020] 优秀的拆分
题干
题目描述
一般来说,一个正整数可以拆分成若干个正整数的和。
例如, 1 = 1 1=1 1=1, 10 = 1 + 2 + 3 + 4 10=1+2+3+4 10=1+2+3+4 等。对于正整数 n n n 的一种特定拆分,我们称它为“优秀的”,当且仅当在这种拆分下, n n n 被分解为了若干个不同的 2 2 2 的正整数次幂。注意,一个数 x x x 能被表示成 2 2 2 的正整数次幂,当且仅当 x x x 能通过正整数个 2 2 2 相乘在一起得到。
例如, 10 = 8 + 2 = 2 3 + 2 1 10=8+2=2^3+2^1 10=8+2=23+21 是一个优秀的拆分。但是, 7 = 4 + 2 + 1 = 2 2 + 2 1 + 2 0 7=4+2+1=2^2+2^1+2^0 7=4+2+1=22+21+20 就不是一个优秀的拆分,因为 1 1 1 不是 2 2 2 的正整数次幂。
现在,给定正整数 n n n,你需要判断这个数的所有拆分中,是否存在优秀的拆分。若存在,请你给出具体的拆分方案。
输入格式
输入只有一行,一个整数 n n n,代表需要判断的数。
输出格式
如果这个数的所有拆分中,存在优秀的拆分。那么,你需要从大到小输出这个拆分中的每一个数,相邻两个数之间用一个空格隔开。可以证明,在规定了拆分数字的顺序后,该拆分方案是唯一的。
若不存在优秀的拆分,输出 -1。
样例 #1
样例输入 #1
6
样例输出 #1
4 2
样例 #2
样例输入 #2
7
样例输出 #2
-1
提示
样例 1 解释
6 = 4 + 2 = 2 2 + 2 1 6=4+2=2^2+2^1 6=4+2=22+21 是一个优秀的拆分。注意, 6 = 2 + 2 + 2 6=2+2+2 6=2+2+2 不是一个优秀的拆分,因为拆分成的 3 3 3 个数不满足每个数互不相同。
数据规模与约定
- 对于 20 % 20\% 20% 的数据, n ≤ 10 n \le 10 n≤10。
- 对于另外 20 % 20\% 20% 的数据,保证 n n n 为奇数。
- 对于另外 20 % 20\% 20% 的数据,保证 n n n 为 2 2 2 的正整数次幂。
- 对于 80 % 80\% 80% 的数据, n ≤ 1024 n \le 1024 n≤1024。
- 对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 10 7 1 \le n \le {10}^7 1≤n≤107。
思路
理解题目
题目说,必须把
n
n
n 分解成
2
2
2 的正整数次幂,即除了拆分成
2
0
2^0
20 即
1
1
1 是不合法的拆分,除此之外都是合法的拆分。那么一个正整数存在
"
优秀的拆分
"
"优秀的拆分"
"优秀的拆分" 的前提是这个数不是奇数!否则一定会拆出
2
0
2^0
20 即
1
1
1 出来,这样的话就不合法了。
并且我们在拆分的时候,还得把
n
n
n 拆分成不同
2
2
2 正整数次幂才行。即
n
=
2
k
1
+
2
k
2
+
2
k
3
+
.
.
.
+
2
k
m
(
k
1
,
k
2
,
k
3
,
.
.
.
k
m
=
1
,
2
,
3
,
4...
)
(
m
=
1
,
2
,
3
,
4...
)
n=2^{k_1}+2^{k_2}+2^{k_3}+...+2^{k_m}(k_1,k_2,k_3,...k_m=1,2,3,4...)(m=1,2,3,4...)
n=2k1+2k2+2k3+...+2km(k1,k2,k3,...km=1,2,3,4...)(m=1,2,3,4...)
第一种方法
那么,第一种方法!我们已知
n
<
=
1
0
7
n<={10^7}
n<=107 ,则
n
n
n 一定在
i
n
t
int
int 的范围内,即在
31
31
31 位二进制以内(因为
i
n
t
int
int 本身有
4
4
4 个字节,即
32
32
32 位用于存储数据,而有一位是符号位,不能用来存储数值,因为只有
31
31
31 位,而最低位的值为
1
1
1 ,则最大值为
2
31
−
1
2^{31}-1
231−1)
那么即使
n
n
n 达到了
i
n
t
int
int 的最大值,拆出的数也不会超过
2
30
2^{30}
230 ,而这种拆分方式拆出一个幂(
2
x
:
x
=
1
,
2
,
3
,
.
.
.
)
2^x:x = 1,2,3,...)
2x:x=1,2,3,...)因为题目要求必须拆成正整数次幂,所以
x
x
x 不能是
0
0
0),就必须尽量先拆出大的幂,因为大的幂可以拆分成小的幂,这样拆除的两个小的幂就一定会重复,如:
8
=
2
3
8=2^3
8=23 ,如果我们把
8
8
8 拆成更小的
2
2
2^2
22 即
4
4
4 ,就会出现如下情况:
8
=
2
2
+
2
2
8=2^2+2^2
8=22+22 ,哪怕一直把所有幂都拆成了
2
2
2 也不行,这就证明了我们的观点是对的。
第二种方法
那么,第二种方法! 学习过计算机基础知识的一定知道 2 2 2 进制,而这种方式刚好符合 2 2 2 进制!即把一个十进制数用很多个幂来表示(二进制),并且这些幂都不可能会重复!(逢二进一)。所以我们只需要按题目要求从高位到低位遍历变量的二进制并且输出即可。
总之
这道题作为
C
S
P
−
J
2020
CSP-J 2020
CSP−J2020 的第一题(签到题)还是挺简单的,到这里就把它轻松秒杀了呀!
具体的实现思路、实现方法都在代码里!!!!!
代码
具体的实现思路、实现方法都在代码里!!!!!
第一种方法
#include <stdio.h>
int n,t ;
//用于输入数据和计算幂
int main(){
scanf("%d",&n) ;
//输入数据
if((n % 2) == 1){
//特判,如果是奇数,则直接输出不可拆分
printf("-1") ;
//输出错误结果-1
return 0 ;
//提前结束程序,这样就不会运行下面的程序了
}
t = 1 ;
//赋初始值,表示 2^0 (二的零次方)
for(int i = 1;i <= 30;++ i)
//循环直到 t 的值为 2^30 为止,循环30次即可
t *= 2 ;
//t 乘二,指数加一
while(t){
//重复执行直到 t 为 0,
//即枚举 int 范围内以 2 为底的幂
if(n >= t){
//因为要优先拆大的幂,所以有幂就得拆
n -= t ;
//减去
printf("%d ",t) ;
//输出这个幂
}
t /= 2 ;//枚举更小的幂
}
return 0 ;
}
第二种方法
#include <stdio.h>
int n ;
//用于输入数据
int main(){
scanf("%d",&n) ;
//输入数据
if(n & 1){ printf("-1") ; return 0 ; }
//如果n为奇数,则输出-1并且提前结束程序
for(int i = 30;i > 0;-- i)
//枚举2^30到2^1
if(n & (1 << i))
//如果n的第i位二进制为1,则可以拆 2^i
//因为二进制中每一位斗都可只能会是0或1,
//则一定不会出现重复的幂
printf("%d ",1 << i) ;
return 0 ;
}
[CSP-J2020] 直播获奖
题干
题目描述
NOI2130 即将举行。为了增加观赏性,CCF 决定逐一评出每个选手的成绩,并直播即时的获奖分数线。本次竞赛的获奖率为 w % w\% w%,即当前排名前 w % w\% w% 的选手的最低成绩就是即时的分数线。
更具体地,若当前已评出了 p p p 个选手的成绩,则当前计划获奖人数为 max ( 1 , ⌊ p × w % ⌋ ) \max(1, \lfloor p \times w \%\rfloor) max(1,⌊p×w%⌋),其中 w w w 是获奖百分比, ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋ 表示对 x x x 向下取整, max ( x , y ) \max(x,y) max(x,y) 表示 x x x 和 y y y 中较大的数。如有选手成绩相同,则所有成绩并列的选手都能获奖,因此实际获奖人数可能比计划中多。
作为评测组的技术人员,请你帮 CCF 写一个直播程序。
输入格式
第一行有两个整数
n
,
w
n, w
n,w。分别代表选手总数与获奖率。
第二行有
n
n
n 个整数,依次代表逐一评出的选手成绩。
输出格式
只有一行,包含 n n n 个非负整数,依次代表选手成绩逐一评出后,即时的获奖分数线。相邻两个整数间用一个空格分隔。
样例 #1
样例输入 #1
10 60
200 300 400 500 600 600 0 300 200 100
样例输出 #1
200 300 400 400 400 500 400 400 300 300
样例 #2
样例输入 #2
10 30
100 100 600 100 100 100 100 100 100 100
样例输出 #2
100 100 600 600 600 600 100 100 100 100
提示
样例 1 解释
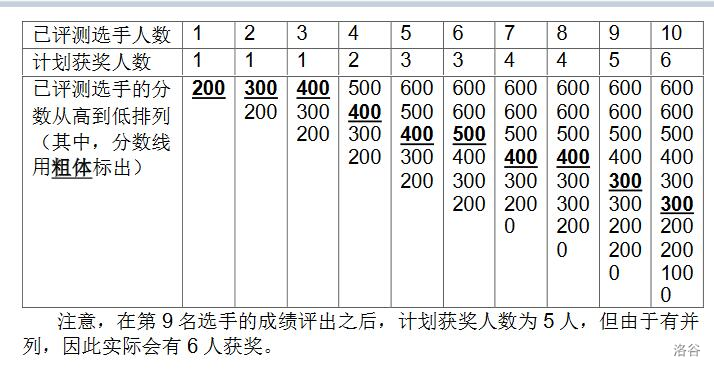
数据规模与约定
各测试点的 n n n 如下表:
| 测试点编号 | n = n= n= |
|---|---|
| 1 ∼ 3 1 \sim 3 1∼3 | 10 10 10 |
| 4 ∼ 6 4 \sim 6 4∼6 | 500 500 500 |
| 7 ∼ 10 7 \sim 10 7∼10 | 2000 2000 2000 |
| 11 ∼ 17 11 \sim 17 11∼17 | 1 0 4 10^4 104 |
| 18 ∼ 20 18 \sim 20 18∼20 | 1 0 5 10^5 105 |
对于所有测试点,每个选手的成绩均为不超过 600 600 600 的非负整数,获奖百分比 w w w 是一个正整数且 1 ≤ w ≤ 99 1 \le w \le 99 1≤w≤99。
提示
在计算计划获奖人数时,如用浮点类型的变量(如 C/C++ 中的 float 、 double,Pascal 中的 real 、 double 、 extended 等)存储获奖比例
w
%
w\%
w%,则计算
5
×
60
%
5 \times 60\%
5×60% 时的结果可能为
3.000001
3.000001
3.000001,也可能为
2.999999
2.999999
2.999999,向下取整后的结果不确定。因此,建议仅使用整型变量,以计算出准确值。
思路
理解题目
题目的意思就是让我们计算出每轮的即时分数线,就是每次输入完数据之后,当前排名前 w % w\% w% 的选手的最低成绩,这就是即时的分数线。
思考
看到这道题,相信每个人的第一思路都是将已经读入的选手成绩做一个排序。但是一看数据范围,
n
<
=
1
0
5
n<=10^5
n<=105
O
(
n
2
∗
l
o
g
n
)
O(n^2*log n)
O(n2∗logn) 的逆天时间复杂度包要超时的。话说有毒蛇,被咬之后,七步必死,但是七步之内,必有解药!
观察数据范围可知,人员的分数总类数竟然比人员总数还要少!!!所以我们就可以在每次输入数据时,使用一个桶去记录下各个分数有多少个人进行桶排序,在从高分到低分遍历一遍桶,即可以
O
(
1
)
O(1)
O(1) 的时间复杂度求出排名前
w
%
w\%
w% 的选手的最低成绩。
具体的实现思路、实现方法都在代码里!!!!!
代码
具体的实现思路、实现方法都在代码里!!!!!
#include <bits/stdc++.h>
using namespace std ;
int n,w,b[605] ;
//分别是参赛总人数,获奖率以及用于桶排序的桶
int main(){
scanf("%d%d",&n,&w) ;
//输入数据
for(int i = 1;i <= n;++ i){
//输入参赛人员的分数
int t = 0 ;
//用于输入的临时变量
scanf("%d",&t) ;
//输入该名选手的分数
++ b[t] ;
//分数 t 的人数加一
int p = max(1,w * i / 100),sum = 0 ;
//p用于计算获奖人数,如果不足1人,则为一人
//sum用于遍历桶
for(int o = 600;o >= 0;-- o){
//从高分往低分遍历
sum += b[o] ;
//计算分数o及以上的有几人
if(sum >= p){
//如果已经够p人了
printf("%d ",o) ;
//则o分的人就是获奖人员中最低分的
//输出他们的分数
break ;
//退出桶的遍历
}
}
}
return 0 ;
}
[CSP-J2020] 表达式
题干
题目描述
小 C 热衷于学习数理逻辑。有一天,他发现了一种特别的逻辑表达式。在这种逻辑表达式中,所有操作数都是变量,且它们的取值只能为 0 0 0 或 1 1 1,运算从左往右进行。如果表达式中有括号,则先计算括号内的子表达式的值。特别的,这种表达式有且仅有以下几种运算:
- 与运算:
a & b。当且仅当 a a a 和 b b b 的值都为 1 1 1 时,该表达式的值为 1 1 1。其余情况该表达式的值为 0 0 0。 - 或运算:
a | b。当且仅当 a a a 和 b b b 的值都为 0 0 0 时,该表达式的值为 0 0 0。其余情况该表达式的值为 1 1 1。 - 取反运算:
!a。当且仅当 a a a 的值为 0 0 0 时,该表达式的值为 1 1 1。其余情况该表达式的值为 0 0 0。
小 C 想知道,给定一个逻辑表达式和其中每一个操作数的初始取值后,再取反某一个操作数的值时,原表达式的值为多少。
为了化简对表达式的处理,我们有如下约定:
表达式将采用后缀表达式的方式输入。
后缀表达式的定义如下:
- 如果 E E E 是一个操作数,则 E E E 的后缀表达式是它本身。
- 如果 E E E 是 E 1 op E 2 E_1~\texttt{op}~E_2 E1 op E2 形式的表达式,其中 op \texttt{op} op 是任何二元操作符,且优先级不高于 E 1 E_1 E1 、 E 2 E_2 E2 中括号外的操作符,则 E E E 的后缀式为 E 1 ′ E 2 ′ op E_1' E_2' \texttt{op} E1′E2′op,其中 E 1 ′ E_1' E1′ 、 E 2 ′ E_2' E2′ 分别为 E 1 E_1 E1、 E 2 E_2 E2 的后缀式。
- 如果 E E E 是 E 1 E_1 E1 形式的表达式,则 E 1 E_1 E1 的后缀式就是 E E E 的后缀式。
同时为了方便,输入中:
- 与运算符(&)、或运算符(|)、取反运算符(!)的左右均有一个空格,但表达式末尾没有空格。
- 操作数由小写字母
x
x
x 与一个正整数拼接而成,正整数表示这个变量的下标。例如:
x10,表示下标为 10 10 10 的变量 x 10 x_{10} x10。数据保证每个变量在表达式中出现恰好一次。
输入格式
第一行包含一个字符串
s
s
s,表示上文描述的表达式。
第二行包含一个正整数
n
n
n,表示表达式中变量的数量。表达式中变量的下标为
1
,
2
,
⋯
,
n
1,2, \cdots , n
1,2,⋯,n。
第三行包含
n
n
n 个整数,第
i
i
i 个整数表示变量
x
i
x_i
xi 的初值。
第四行包含一个正整数
q
q
q,表示询问的个数。
接下来
q
q
q 行,每行一个正整数,表示需要取反的变量的下标。注意,每一个询问的修改都是临时的,即之前询问中的修改不会对后续的询问造成影响。
数据保证输入的表达式合法。变量的初值为
0
0
0 或
1
1
1。
输出格式
输出一共有 q q q 行,每行一个 0 0 0 或 1 1 1,表示该询问下表达式的值。
样例 #1
样例输入 #1
x1 x2 & x3 |
3
1 0 1
3
1
2
3
样例输出 #1
1
1
0
样例 #2
样例输入 #2
x1 ! x2 x4 | x3 x5 ! & & ! &
5
0 1 0 1 1
3
1
3
5
样例输出 #2
0
1
1
提示
样例 1 解释
该后缀表达式的中缀表达式形式为 ( x 1 and x 2 ) or x 3 (x_1 \operatorname{and} x_2) \operatorname{or} x_3 (x1andx2)orx3。
- 对于第一次询问,将 x 1 x_1 x1 的值取反。此时,三个操作数对应的赋值依次为 0 0 0, 0 0 0, 1 1 1。原表达式的值为 ( 0 & 0 ) ∣ 1 = 1 (0\&0)|1=1 (0&0)∣1=1。
- 对于第二次询问,将 x 2 x_2 x2 的值取反。此时,三个操作数对应的赋值依次为 1 1 1, 1 1 1, 1 1 1。原表达式的值为 ( 1 & 1 ) ∣ 1 = 1 (1\&1)|1=1 (1&1)∣1=1。
- 对于第三次询问,将 x 3 x_3 x3 的值取反。此时,三个操作数对应的赋值依次为 1 1 1, 0 0 0, 0 0 0。原表达式的值为 ( 1 & 0 ) ∣ 0 = 0 (1\&0)|0=0 (1&0)∣0=0。
样例 2 解释
该表达式的中缀表达式形式为 ( not x 1 ) and ( not ( ( x 2 or x 4 ) and ( x 3 and ( not x 5 ) ) ) ) (\operatorname{not}x_1)\operatorname{and}(\operatorname{not}((x_2\operatorname{or}x_4)\operatorname{and}(x_3\operatorname{and}(\operatorname{not}x_5)))) (notx1)and(not((x2orx4)and(x3and(notx5))))。
数据规模与约定
- 对于 20 % 20\% 20% 的数据,表达式中有且仅有与运算(&)或者或运算(|)。
- 对于另外 30 % 30\% 30% 的数据, ∣ s ∣ ≤ 1000 |s| \le 1000 ∣s∣≤1000, q ≤ 1000 q \le 1000 q≤1000, n ≤ 1000 n \le 1000 n≤1000。
- 对于另外 20 % 20\% 20% 的数据,变量的初值全为 0 0 0 或全为 1 1 1。
- 对于 100 % 100\% 100% 的数据, 1 ≤ ∣ s ∣ ≤ 1 × 1 0 6 1 \le |s| \le 1 \times 10^6 1≤∣s∣≤1×106, 1 ≤ q ≤ 1 × 1 0 5 1 \le q \le 1 \times 10^5 1≤q≤1×105, 2 ≤ n ≤ 1 × 1 0 5 2 \le n \le 1 \times 10^5 2≤n≤1×105。
其中, ∣ s ∣ |s| ∣s∣ 表示字符串 s s s 的长度。
思路
前方高能!!!请认真进行”头脑风暴“!!!
理解题目
后缀表达式又叫做逆波兰表达式,是一种没有括号,并严格遵循“从左到右”运算的后缀式表达方法。所以计算逆波兰表达式我们需要严格遵守以下规则进行计算:
如果当前字符为变量或者为数字,则压栈,如果是运算符,则将栈顶两个元素弹出作相应运算,结果再入栈,最后当表达式扫描完后,栈里的就是结果。
而题目就是给出了一个后缀表达式,让我们计算其中的各个变量为各种取值时的值
思考
而看到题目的数据范围,我们就可以知道用刚刚所说的一般的方法去计算一定是不行的了。而我们可以很轻易的发现,题目中,每次进行询问都只会改变一个变量的值,并且每一个变量在表达式中只会出现一次。这里我们需要引入一个概念:短路
就像是以下的这一条语句,就会进行短路
if(1 || (a += 1))
是不是以为这个
i
f
if
if 语句会先把所有值都求出来在进行判断?可事实上,这是错误的。它只会求出
1
1
1 的值之后,就发现了无论后边一个值为什么,结果一定都是为真的。所以后面部分的
a
+
=
1
a += 1
a+=1 表达式实际上并不会进行求值。那么我们就把这个语句称作“废物表达式”。
我们可以先预处理一遍求出原表达式的值,再预处理出有哪些表达式属于“废物表达式”。如果改变的变量所改变的表达式是“废物表达式”的话,那么结果就不会变(因为这个表达式是”废物“,所以不会影响值)否则,新表达式的值会与原表达式值相反。让我们来试一试吧!
x1 x2 & x3 |
经过预处理得知,原表达式的值为
(1 & 0) | 1即
1
1
1
在每次只能改变一个变量的情况下,表达式 (1 & 0)就是一个“废物”,无论它的值是什么,由于操作符 |的右项是1所以无论如何,整个表达式的值都不会变,为1。
所以当
x
1
,
x
2
x1,x2
x1,x2 的值取反时,并不会影响最终结果。而当
x
3
x3
x3 的值取反时,最终结果就会改变。
具体实现
1.输入
首先要把全部的表达式部分输入进去。通过样例可知,表达式每一个部分的第一个字符都不可能是字符,无论是变量(
x
n
xn
xn),与运算(
&
\&
&),或运算(
∣
|
∣),非运算(
1
1
1),它们的首字符都不是数字,所以我们就可以以此判断当前输入的是表达式还是已经输入到
n
n
n 了。为了处理方便,我们使用一个
i
n
t
int
int 类型的
a
a
a 数组,表达式的每一个部分,如果是变量,则把它的编号(
x
x
x后的数)放入
a
a
a 数组,并且使用
p
o
s
pos
pos 数组记录下这个变量在表达式中的位置(形式:
p
o
s
[
编号
]
=
位置
pos[编号]=位置
pos[编号]=位置)。否则将这个运算符的
A
S
C
A
L
L
ASCALL
ASCALL码的相反数(正数变负数,负数变正数)存入
a
a
a 数组,并且使用
p
o
s
pos
pos 数组记录下这个运算符在表达式中的位置(形式:
p
o
s
[
编号
]
=
位置
pos[编号]=位置
pos[编号]=位置。在读取
a
a
a 数组的时候通过判断
a
[
i
]
a[i]
a[i] 的正负数即可判断它是变量还是运算符。
输入每个变量的初始值。
Tips:在获取变量编号及
n
n
n的值的时候可以使用
s
s
c
a
n
f
sscanf
sscanf,它的用法和
s
c
a
n
f
scanf
scanf 函数类似,但是
s
s
c
a
n
f
sscanf
sscanf 是从字符串中读取数据,格式为
s
s
c
a
n
f
(
源字符串,格式控制符,
.
.
.
(
变量地址
)
)
sscanf(源字符串,格式控制符,...(变量地址))
sscanf(源字符串,格式控制符,...(变量地址))。例如:
s
s
c
a
n
f
(
"
x
25
"
,
“
x
%
d
”
,
&
t
)
sscanf("x25",“x\%d”,\&t)
sscanf("x25",“x%d”,&t),这条语句就会让
t
t
t 读取到
25
25
25 的值。非常好用!!!
2.预处理
我们需要一个栈
o
p
op
op 用来求出原表达式的值,并且这个栈的栈元素类型得要是
p
a
i
r
<
b
o
o
l
,
i
n
t
>
pair<bool,int>
pair<bool,int>,这个类型表示一种结构体类型,有两个结构体成员,第一个结构体成员
f
i
r
s
t
first
first的类型为
b
o
o
l
bool
bool,第二个结构体成员
s
e
c
o
n
d
second
second的类型为
i
n
t
int
int。这两个结构体成员分别用于存储表达式的值和位置。这里
表达式的位置
表达式的位置
表达式的位置指的是一个后缀表达式中最后一个运算符的位置(若本身就只有一个变量,则指这个变量的位置)。
遍历
a
a
a 数组。如果当前
a
[
i
]
a[i]
a[i]为变量或者为数字,则压栈。如果是
!
!
!运算符,则将栈顶一个元素弹出作相应运算,结果再入栈。关键的是
&
或
∣
\&或|
&或∣运算符,则将栈顶两个元素弹出作相应运算,结果再入栈。在这过程当中,如果有一方的值可以满足无论另一方怎么改变都不会让结果改变,那么就给这另一方表达式打上“废物”标记。可以使用一个数组
l
a
z
y
lazy
lazy 来实现,形式为(
l
a
z
y
[
表达式位置
]
=
是否是废物表达式
lazy[表达式位置]=是否是废物表达式
lazy[表达式位置]=是否是废物表达式)。在整个表达式扫描的过程中,我们还得使用
n
e
x
nex
nex数组来存储包含当前表达式的最早出现的表达式是哪个。例如:表达式(
x
1
x
2
&
x
3
∣
x1x2\&x3|
x1x2&x3∣)中,最早包含表达式(
x
1
x
2
&
x1x2\&
x1x2&)的表达式是表达式(
x
1
x
2
&
x
3
∣
x1x2\&x3|
x1x2&x3∣),所以
n
e
x
[
表达式
x
1
x
2
&
的位置
]
=
表达式
x
1
x
2
&
x
3
∣
的位置
nex[表达式x1x2\&的位置]=表达式x1x2\&x3|的位置
nex[表达式x1x2&的位置]=表达式x1x2&x3∣的位置。最后当表达式扫描完后,栈里的就是结果。
预处理
最后,要判断某个变量在不在“废物表达式”当中,只要使用
n
e
x
nex
nex数组判断判断先后包含这个变量的表达式是不是“废物表达式”即可。如果是,输出原结果,否则输出与原结果相反的结果。
具体的实现思路、实现方法都在代码里!!!!!
代码
具体的实现思路、实现方法都在代码里!!!!!
#include <bits/stdc++.h>
using namespace std ;
#define N (500005)
string s ;
//用于输入的字符串
int l,n,q,a[N],x[N],nex[N],pos[N],lazy[N] ;
//一些变量,l表示表达式当前输入了多少个字符串
//n表示变量个数,q表示询问次数,x存储各个变量的原值
//a存储表达式,符号用负数表示,变量用正数表示
//nex存储一个表达式所对应下一步的运算符在a中的位置
//pos存储各个变量在a中的位置
stack<pair<bool,int> > op ;
//用于计算表达式的值
int to_int(string& s){ int t ; sscanf(s.c_str(),"x%d",&t) ; return t ; }
//用于获取变量名的编号,如:x1 返回 1
//sscanf用法和scanf类似,但是是从字符串中读取
int main(){
ios::sync_with_stdio(false) ;
cin.tie(0) ;
//关闭流同步,提升cin、cout的速度
cin >> s ;
//输入表达式的第一个值
a[++ l] = to_int(s),pos[a[l]] = l ;
//第一个一定是变量,记录下这个变量的编号和位置
for(int i = 2;cin >> s && (s[0] > '9' || s[0] < '0');++ i)
//重复执行直到所输入字符串的是第一位是数字
//也就是输入到了数字,即n
if(s[0] == 'x')a[++ l] = to_int(s),pos[a[l]] = l ;
//如果是变量,记录下这个变量的编号和位置
else a[++ l] = -s[0] ;
//否则,记录下这个符号是什么
sscanf(s.c_str(),"%d",&n) ;
//从字符串中读出n的值
for(int i = 1;i <= n;++ i)cin >> x[i] ;
//输入各个变量的原值,计算原表达式的值
for(int i = 1;i <= l;++ i){
//遍历表示表达式的a数组
if(a[i] > 0) op.push({x[a[i]],i}) ;
//如果存储的是整数,则表示变量编号
//保存下变量的值和位置即可
else {
//否则,存储的是运算符ascall码的相反数
//(正负相反,正变负,负变正)
pair<int,int> t = op.top() ;
//获取当前栈顶的值
nex[t.second] = i ;
//标记:这个表达式对应的下一个运算
//是当前位置的运算
if(a[i] == -'!')t.first = !t.first ;
//如果是取反符号,则取反它的值
else{
op.pop() ;
//弹栈,当前栈顶表示更早入栈的值
if(a[i] == -'&'){
//如果是与符号
//因为只能改变一个变量,
//所以两个表达式也最多只会改变一个
if(!op.top().first)lazy[t.second] = 1 ;
//那么如果一个值是假,那么结果就一定为假
if(!t.first)lazy[op.top().second] = 1 ;
//如果一个值是假,那么结果就一定为假
//只要标记这个表达式最后运算符的位置即可
//只需要判断运算符在不在某个“废物表达式”其中即可
//即根据nex一直寻找每次经过的运算,
//看一看这个经过的运算所构成的表达式
//是不是“废物表达式”即可
t.first &= op.top().first ;
//计算结果
}else{
//否则是或运算
if(op.top().first)lazy[t.second] = 1 ;
//同上,如果一个为真,结果一定为真,另一个是“废物”
if(t.first)lazy[op.top().second] = 1 ;
//同上,如果一个为真,结果一定为真,另一个是“废物”
t.first |= op.top().first ;
//计算结果
}
nex[op.top().second] = i ;
//记录下栈顶
}
op.pop() ;
//退栈
op.push({t.first,i}) ;
//将当前结果入栈
}
}
cin >> q ;
//输入询问次数
for(int i = 1;i <= q;++ i){
int t = 0 ;
//临时变量
cin >> t ;
//输入要将哪个变量的值取反
t = pos[t] ;
//获取这个变量的位置
while(t != l && !lazy[t])t = nex[t] ;
//遍历这个变量所参与到构成的所有表达式中有没有
//“废物表达式”
cout << int(op.top().first ^ !lazy[t]) << '\n' ;
//如果有,就过取反,否则结果不变。
//这里使用异或运算来实现
}
return 0 ;
}
[CSP-J2020] 方格取数
题干
题目描述
设有 n × m n \times m n×m 的方格图,每个方格中都有一个整数。现有一只小熊,想从图的左上角走到右下角,每一步只能向上、向下或向右走一格,并且不能重复经过已经走过的方格,也不能走出边界。小熊会取走所有经过的方格中的整数,求它能取到的整数之和的最大值。
输入格式
第一行有两个整数 n , m n, m n,m。
接下来 n n n 行每行 m m m 个整数,依次代表每个方格中的整数。
输出格式
一个整数,表示小熊能取到的整数之和的最大值。
样例 #1
样例输入 #1
3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1
样例输出 #1
9
样例 #2
样例输入 #2
2 5
-1 -1 -3 -2 -7
-2 -1 -4 -1 -2
样例输出 #2
-10
提示
样例 1 解释
样例 2 解释
数据规模与约定
- 对于 20 % 20\% 20% 的数据, n , m ≤ 5 n, m \le 5 n,m≤5。
- 对于 40 % 40\% 40% 的数据, n , m ≤ 50 n, m \le 50 n,m≤50。
- 对于 70 % 70\% 70% 的数据, n , m ≤ 300 n, m \le 300 n,m≤300。
- 对于 100 % 100\% 100% 的数据, 1 ≤ n , m ≤ 1 0 3 1 \le n,m \le 10^3 1≤n,m≤103。方格中整数的绝对值不超过 1 0 4 10^4 104。
2024/2/4 添加一组 hack 数据。
思路
理解题目
就是要求最大路径和,并且和传统的路径和题目不一样,可以向上、向下,向右走。
思考
只能向右不能向左,可以发现每一列都是可以单独求解的,而每一列都只单独与上一列有关联,则我们可以使用动态规划,通过上一列来推出下一列。
具体实现:我们用数组
a
a
a保存各个格子的值。因为上下两个方向都有,所以我们总共使用两个数组进行动态规划:
u
p
,
d
o
w
n
up,down
up,down,它们分别表示从上面、下面走到位置
(
i
,
o
)
(i,o)
(i,o)时的最大值,再用数组
f
f
f表示走到位置
(
i
,
o
)
(i,o)
(i,o)的最大值,很容易就可以得出状态转移方程:
初始值:
f
[
1
]
[
1
]
=
a
[
1
]
[
1
]
,
f
[
i
]
[
1
]
=
f
[
i
−
1
]
+
a
[
i
]
[
1
]
f[1][1]=a[1][1],f[i][1]=f[i-1]+a[i][1]
f[1][1]=a[1][1],f[i][1]=f[i−1]+a[i][1]
u
p
[
1
]
[
o
]
=
(
f
[
1
]
[
o
−
1
]
+
a
[
1
]
[
o
]
)
,
d
o
w
n
[
n
]
[
o
]
=
(
f
[
n
]
[
o
−
1
]
+
a
[
n
]
[
o
]
)
up[1][o]=(f[1][o-1]+a[1][o]),down[n][o]=(f[n][o-1]+a[n][o])
up[1][o]=(f[1][o−1]+a[1][o]),down[n][o]=(f[n][o−1]+a[n][o])
u
p
[
i
]
[
o
]
=
m
a
x
(
u
p
[
i
−
1
]
[
o
]
,
f
[
i
]
[
o
−
1
]
)
+
a
[
i
]
[
o
]
up[i][o]=max(up[i-1][o],f[i][o-1])+a[i][o]
up[i][o]=max(up[i−1][o],f[i][o−1])+a[i][o]
d
o
w
n
[
i
]
[
o
]
=
m
a
x
(
d
o
w
n
[
i
+
1
]
[
o
]
,
f
[
i
]
[
o
−
1
]
)
+
a
[
i
]
[
o
]
down[i][o]=max(down[i+1][o],f[i][o-1])+a[i][o]
down[i][o]=max(down[i+1][o],f[i][o−1])+a[i][o]
f
[
i
]
[
o
]
=
m
a
x
(
u
p
[
i
]
[
o
]
,
d
o
w
n
[
i
]
[
o
]
)
f[i][o]=max(up[i][o],down[i][o])
f[i][o]=max(up[i][o],down[i][o])
注:
m
a
x
(
a
,
b
)
表示
a
,
b
中的大值
注:max(a,b)表示a,b中的大值
注:max(a,b)表示a,b中的大值
而最终的答案就是
f
[
n
]
[
m
]
f[n][m]
f[n][m]
很容易可以看出,又因为每一列的结果都只与上一列的最终最有值即
f
f
f数组有关,所以我们可以再进行一些优化,把
u
p
,
d
o
w
n
,
f
up,down,f
up,down,f从二维数组优化到一维数组。即先用上一列的
f
f
f数组把这一列的
u
p
.
d
o
w
n
up.down
up.down数组的值推出来,再用
u
p
,
d
o
w
n
up,down
up,down数组把
f
f
f数组推出来即可。(一定要按照这个顺序!)
初始值:
f
[
1
]
=
a
[
1
]
[
1
]
,
f
[
i
]
=
f
[
i
−
1
]
+
a
[
i
]
[
1
]
f[1]=a[1][1],f[i]=f[i-1]+a[i][1]
f[1]=a[1][1],f[i]=f[i−1]+a[i][1]
u
p
[
1
]
=
(
f
[
1
]
+
a
[
1
]
)
,
d
o
w
n
[
n
]
=
(
f
[
n
]
+
a
[
n
]
)
up[1]=(f[1]+a[1]),down[n]=(f[n]+a[n])
up[1]=(f[1]+a[1]),down[n]=(f[n]+a[n])(未进行更新操作的旧
f
f
f)
u
p
[
i
]
=
m
a
x
(
u
p
[
i
−
1
]
,
f
[
i
]
)
+
a
[
i
]
[
o
]
up[i]=max(up[i-1],f[i])+a[i][o]
up[i]=max(up[i−1],f[i])+a[i][o]
d
o
w
n
[
i
]
=
m
a
x
(
d
o
w
n
[
i
+
1
]
,
f
[
i
]
)
+
a
[
i
]
[
o
]
down[i]=max(down[i+1],f[i])+a[i][o]
down[i]=max(down[i+1],f[i])+a[i][o]
f
[
i
]
=
m
a
x
(
u
p
[
i
]
,
d
o
w
n
[
i
]
)
f[i]=max(up[i],down[i])
f[i]=max(up[i],down[i])
注:
m
a
x
(
a
,
b
)
表示
a
,
b
中的大值
注:max(a,b)表示a,b中的大值
注:max(a,b)表示a,b中的大值
而最终的答案就是
f
[
n
]
f[n]
f[n]
代码
#include <stdio.h>
#define N (1005)
long long max(long long a,long long b){ return (a > b) ? (a) : (b) ; }
//返回两者大值
long long n,m,a[N][N],up[N],down[N],f[N] ;
//变量丁定义
int main(){
scanf("%lld%lld",&n,&m) ;
//输入行、列
for(int i = 1;i <= n;++ i)
for(int o = 1;o <= m;++ o)
scanf("%lld",&a[i][o]) ;
//输入各个格子的值
f[1] = a[1][1] ;
for(int i = 2;i <= n;++ i)f[i] = f[i - 1] + a[i][1] ;
//初始化f
for(int o = 2;o <= m;++ o){
down[1] = f[1] + a[1][o] ; up[n] = f[n] + a[n][o] ;
//初始化down,up
for(int i = 2;i <= n;++ i)down[i] = max(down[i - 1],f[i]) + a[i][o] ;
//更新down
for(int i = n - 1;i > 0;-- i)up[i] = max(up[i + 1],f[i]) + a[i][o] ;
//更新up
for(int i = 1;i <= n;++ i)f[i] = max(down[i],up[i]) ;
//更新f
}
printf("%lld",f[n]) ;
//输出答案
return 0 ;
}
尾声
又成功地“秒杀”了一年的CSP/NOIP,祝读者水平高升,参加竞赛都能“秒杀”取得好成绩!
























 2102
2102

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








