《算法导论》笔记－－二叉搜索树

   

　　二叉搜索树（binary search tree）是经过一定地组织形成的有特定结构特征的二叉树，支持各种动态集合（dynamic set）操作（如insert、delete、maximum、minimum等等）。这些操作的时间复杂度与树的高度成正比。一棵有n个节点的完全二叉树（complete binary tree）的高度不超过lgn。因此，对于完全二叉树的这些操作的最坏时间复杂度（worst-case time）为O(lgn)。但极端病态的二叉树，形状就与链表是一样的，那么，各项操作的最坏时间复杂度将变为O(n)。

　　由随机输入数据构建的二叉搜索树的期望高度是O(lgn)，也有一些经过更加复杂的构造规则而得到的二叉查找树（如红黑树、B树等），对于一般的输入都可以保持O(lgn)的期望高度。

　　二叉搜索树的结构特征是：对于一个节点x，它的键值为key[x]，那么x的左子树中的任何一个节点的键值，都不会大于key[x]，x的右子树中的任何一个节点的键值都不会小于key[x]。

　　用C代码进行实现一个二叉搜索树，树的节点只存储int型的键值，并实现动态集合的基本操作，作为练习应该是OK了，呵呵。

　　先定义一些基本的结构，像树的节点、对节点的基本操作，用于取节点的左右子节点和父节点、以及一个树“对象”：

// 树节点 typedef struct tagBSTreeNode { int key; struct tagBSTreeNode *left; struct tagBSTreeNode *right; struct tagBSTreeNode *parent; }BSTreeNode, *PBSTreeNode; #define GetLeft(pNode) (pNode->left) // 左子节点 #define GetRight(pNode) (pNode->right) // 右子节点 #define GetParent(pNode) (pNode->parent) // 父节点 // 二叉查找树“对象” typedef struct tagBSTree { PBSTreeNode root; }BSTree, *PBSTree;

二叉搜索树的节点插入操作

将一个节点插入二叉搜索树，且要保持二叉搜索树的结构特征，关键是要找到合适插入的位置。
所以，插入操作时，先进行位置地查找，方法是从根开始，比较要插入的节点的键值与树中的每一个节点的键值，如果大于该节点，则下一个比较的位置移到该节点的右子节点。否则，下一个比较的位置移到该节点的左子节点上。这样一直比较到树的最“底下”的节点X（叶节点）。然后视键值，把需要插入的节点设置为 X的左子点，或是右子节点。代码如下：

void TREE_INSERT(PBSTree pTree, PBSTreeNode pNode) { PBSTreeNode pNodePosition = pTree->root; PBSTreeNode pParent = NULL; while (NULL != pNodePosition) { // 找到插入的位置 pParent = pNodePosition; pNodePosition = (pNode->key > pNodePosition->key ? GetRight(pNodePosition) : GetLeft(pNodePosition)); } pNode->parent = pParent; if (NULL == pParent) { // 对于根节点的特殊处理 pTree->root = pNode; return ; } else { // 非根节点时 if (pNode->key > pParent->key) { pParent->right = pNode; } else { pParent->left = pNode; } } }

    最大值与最小值。

对于二叉搜索树，很容易找到最大值和最小值。只需要从根节点开始，不断地向左子节点移到，到叶子，就是最小值。从根节点开始，不断地向右子节点移到，到叶子，就是最大值。

PBSTreeNode TREE_MAX(PBSTreeNode pRoot) { while (NULL != GetRight(pRoot)) { pRoot = GetRight(pRoot); } return pRoot; } PBSTreeNode TREE_MIN(PBSTreeNode pRoot) { while (NULL != GetLeft(pRoot)) { pRoot = GetLeft(pRoot); } return pRoot; }

 

  直接前趋
节点X的直接前趋节点Y，就在树中，键值比X小，但又最接近X的节点。
如果找到直接前趋节点呢？
１．首先，如果节点X有左子节点，那么，X的直接前趋节点Y一定是以X的左子节点为根的子树中的最大键值节点。
证明，如下图，图中从X节点向上的路径可能出现的两种情况，我们称1是向左，２是向右。

 

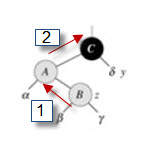
设X是黑色节点。从X向树的上方攀登，只要是沿着右方向到达的节点（如果图中2），都是键值比X大的节点（根据二叉查找树的性质，左子树中的任何节点都小于根嘛），所以这些节点不可能是X的前趋（因为前趋节点的键值是小于X的）。如果沿着左方向到达的节点（如图中1），那这个节点的键值确实比X的键值小，但是，它也绝不可能是X的直接前趋，因为X以及X的子节点，都是这个节点（Z）的右子树中的节点，所以Z的键值一定小于X的左子树中的任何一个节点的键值，那么它就失去作为X直接前趋的资格了（因为直接前趋是应该是键值最接近X的嘛）。对称地，X是父节点的右节点时，情况也是一样的。所以可以得出结论，如果节点X有左子节点，那么X的直接前趋节点Y一定是以X的左子节点为根的子树中的最大键值节点。
２．如果X没有左子树呢？那么，从上面的分析可知，X的直接前趋就一定是从X向上的路径中，第一次“左”转时的节点Z。如果向上直到根节点的路径都是右方向的，那么这个X节点就没有直接前趋节点了（也就是X是这二叉查找树最小的节点）。

 

  直接后继
直接后继就只给出结论了：如果节点X有右子节点，那么，X的直接前趋节点Y一定是以X的左子节点为根的子树中的最小键值节点。如果没有右子节点，那么X的直接后继节点就是从X向上的路径中第一次右转时的节点。
证明与直接前趋是对称的。

 

PBSTreeNode TREE_SUCCESSOR(PBSTreeNode pRoot) { if (NULL != GetRight(pRoot)) { return TREE_MIN(GetRight(pRoot)); } PBSTreeNode pParent = GetParent(pRoot); while((NULL != pParent) && (pRoot == GetRight(pParent))) { pRoot = pParent; pParent = GetParent(pRoot); } return pParent; } PBSTreeNode TREE_PREDECESSOR(PBSTreeNode pRoot) { if (NULL != GetLeft(pRoot)) { return TREE_MAX(GetLeft(pRoot)); } PBSTreeNode pParent = GetParent(pRoot); while((NULL != pParent) && (pRoot == GetLeft(pParent))) { pRoot = pParent; pParent = GetParent(pRoot); } return pParent; }  

 

  查找 

 

 

其实二叉查找树的查找，应该很容易理解了，就是让X指向根，比较X的键值是否与要找的键值相等，是，那么X就要找的节点，如果不是，那么X就根据值的大小向左或向右移动，以此不断地向下，直到树的末尾。

PBSTreeNode TREE_SEARCH(PBSTreeNode pRoot, int val_key) { while ((NULL != pRoot) && (val_key != pRoot->key)) { pRoot = (val_key < pRoot->key ? GetLeft(pRoot) : GetRight(pRoot)); } return pRoot; }

 

  删除：

删除一个节点，最重要的也是想办法在删除动作后，仍然保持二叉查找树的特征。

当然，我们会想用最容易的方法来保持它（复杂的话，就成有名有姓的树了，像红黑树，在保证这二叉查基本特征时，还维持了一些其它的特性，那就复杂鸟）。分三种情况：

１．如果被删除的节点没有子树，好说，直接删除就可以了，对二叉搜索树的基本特征没有任何影响。

２．如果被删除的节点，只有一个子树呢？也好说，把那唯一的子树挂到需要删除节点的父节点上相应的子树位置，然后删除掉需要删除的节点。也不会对二叉树的基本特征产生不良影响。

３．如果被删除节点有两个子树呢？那就不好办了，关键是要保住树的基本性质不动摇，呵呵。怎么办呢？
我想，先化为已经解决的问题，那不就好办了吗？hoho，１和２是已经解决的，那么化为１或２来解决嘛。设要删除的子节点是X，那么我们随意选取一个子树，从底部开始，把这子树上所有的节点，一个一个从树上“摘下来”，存着。然后X就成为一个只有一颗子树的节点，然后就适用第２种情况啦。删除完X后，再把存着的那些节点重新插入到树上，不就得了。呵呵，笨办法，但我确实这么想过。
再想想其它办法。要想不影响树的特性，那么最简单的想法是如果能只动X以及X以下的节点，那么树的其它部分肯定是OK的。那只要处理X以及X的子树就行了。想想，如果能在子树中找一个节点来替代X的位置，并保证新的子树也是满足二叉查找树要求的，这样改动量可能就比较小了。那么找哪个节点来代替它呢？当然是键值最接近X的，这样二叉树的特征就比较容易保持嘛。键值最接近X的，上面已经说过了，就是直接前趋和直接后继。正好，对于有两个子树的X来说，它的直接前趋和直接后继都是在它的子树中的，分别是左子树的最大值、右子树的最小值。而且，从子树中取下这两个节点（取下来干嘛？代替需要删除的X节点呗），也是比较容易的，因为“最大”“最小”值节点，最多拥有不超过一个子节点（不然它绝对不够格做最大或最小）。而没有子节点和只有一个子节点的节点删除，是我们已经会啦~~~。好，那么就取前趋或后继就来代替需要删除的节点，问题就解决了。

PBSTreeNode TREE_DELETE(PBSTree pTree, PBSTreeNode pDel) { PBSTreeNode pRelDel; if ((NULL == GetLeft(pDel)) || (NULL == GetLeft(pDel))) { pRelDel = pDel; } else { pRelDel = TREE_SUCCESSOR(pDel); } PBSTreeNode pChildOfDel; pChildOfDel = (GetLeft(pRelDel)!= NULL ? GetLeft(pRelDel) : GetRight(pRelDel)); if (pChildOfDel != NULL) { SetParent(pChildOfDel, GetParent(pRelDel)); } if (NULL == GetParent(pRelDel)) { pTree->root = pChildOfDel; } else { if (pRelDel == GetLeft(GetParent(pRelDel))){ SetLeft(GetParent(pRelDel), pChildOfDel); } else { SetRight(GetParent(pRelDel), pChildOfDel); } } if (pRelDel != pDel) { pDel->key = pRelDel->key; } return pRelDel; }