一、回归函数及目标函数
以均方误差作为目标函数(损失函数),目的是使其值最小化,用于优化上式。
二、优化方式(Gradient Descent)
1、最速梯度下降法
也叫批量梯度下降法Batch Gradient Descent,BSD
a、对目标函数求导
b、沿导数相反方向移动theta
原因:
(1)对于目标函数,theta的移动量应当如下,其中a为步长,p为方向向量。
(2)对J(theta)做一阶泰勒级数展开:
(3)上式中,ak是步长,为正数,可知要使得目标函数变小,则 应当<0,并且其绝对值应当越大越好,这样下降的速度更快。在泰勒级数中,g代表J(theta k)的梯度,所以为了使得
应当<0,并且其绝对值应当越大越好,这样下降的速度更快。在泰勒级数中,g代表J(theta k)的梯度,所以为了使得 为负并且绝对值最大,应当使theta的移动方向与梯度g相反。
为负并且绝对值最大,应当使theta的移动方向与梯度g相反。
2、随机梯度下降法(stochastic gradient descent,SGD)
SGD是最速梯度下降法的变种。
使用最速梯度下降法,将进行N次迭代,直到目标函数收敛,或者到达某个既定的收敛界限。每次迭代都将对m个样本进行计算,计算量大。
为了简便计算,SGD每次迭代仅对一个样本计算梯度,直到收敛。伪代码如下(以下仅为一个loop,实际上可以有多个这样的loop,直到收敛):
(1)由于SGD每次迭代只使用一个训练样本,因此这种方法也可用作online learning。
(2)每次只使用一个样本迭代,若遇上噪声则容易陷入局部最优解。
3、Mini-batch Gradient Descent
(1)这是介于BSD和SGD之间的一种优化算法。每次选取一定量的训练样本进行迭代。
(2)从公式上似乎可以得出以下分析:速度比BSD快,比SGD慢;精度比BSD低,比SGD高。
4、带Mini-batch的SGD
(1)选择n个训练样本(n<m,m为总训练集样本数)
(2)在这n个样本中进行n次迭代,每次使用1个样本
(3)对n次迭代得出的n个gradient进行加权平均再并求和,作为这一次mini-batch下降梯度
(4)不断在训练集中重复以上步骤,直到收敛。








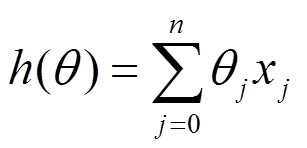
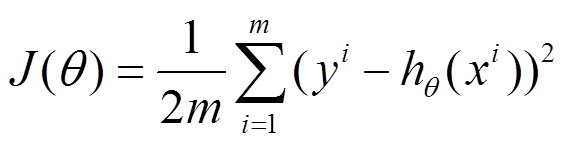
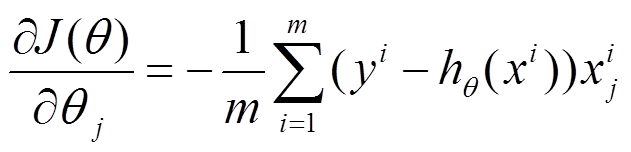
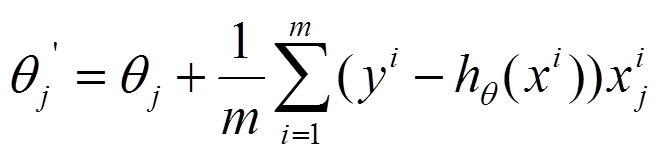
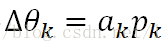
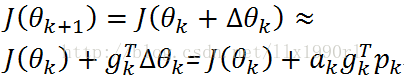
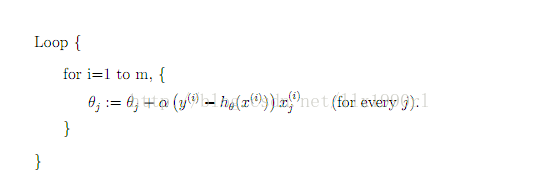














 1443
1443

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








