一、基本思想
把区间逐次二分,反复利用复化求积公式进行计算,直至二分前后的两次积分近似值之差符合精度要求为止。采用误差的“事后估计”方法进行步长的自动选择。
以复化梯形公式为例,设将求积区间[a,b]进行n等分,共有n+1个互异节点xk(k=0,1,...,n),按公式(1.1)计算Tn,共需计算n+1个节点处的函数值 f(xk) (k=0,1,...,n)。若将求积区间再二分一次,则等分点为2n+1个,新增节点为n个。记[xk,xk+1](k=0,1,...,n-1)为二分前的求积子区间,二分后新增节点为xk+1/2 = (xk+xk+1)/2 (k=0,1,...,n-1)。利用复化梯形公式计算[xk,xk+1]上的积分近似值为式(1.2)。
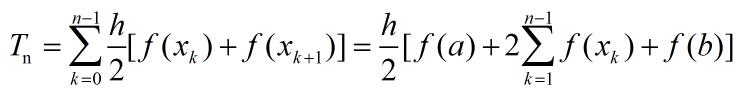
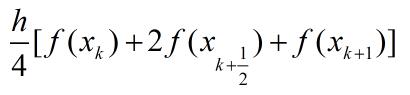
其中h=(b-a)/n代表二分前的步长,将每个子区间的积分近似值相加得:
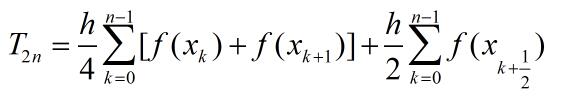
利用Tn的计算公式,可得递推公式:
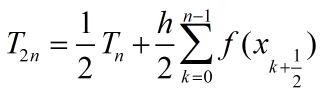
误差:
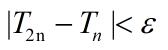
二、示例函数
此处以f(x)=sinx/x为例进行说明,读者可以根据自己的需要修改f(x)。
示例函数实现代码:
%计算x对应的函数值f(x)
function [y_x] = CalcuFunctionValue(x)
% inputs:
% x:待求值
% outputs:
% y_x:x对应的函数值
% 根据极限计算,当x→0时,y_x→1.
if x == 0
y_x = 1;
else
y_x = sin(x)/x;
end
end三、自适应步长求积的实现
根据上述递推公式1.4和误差不等式1.5,将误差不等式判断作为循环结束的条件。
实现代码:
%% 自适应步长复化梯度求积
function [result] = AdaptiveStepIntegral(x_LowBound,x_UpBound,accuracyValue)
% 2017-11-03 xh_scu 1270978696@qq.com
% inputs:
% x_LowBound:求积区间的下界
% x_UpBound :求积区间的上界
% accuracyValue:精度值
% outputs:
% result:输出一个维数组,对应每一次二分得到的结果,长度为m+1
%计算f(a)和f(b)
f_0 = CalcuFunctionValue(x_LowBound);
f_1 = CalcuFunctionValue(x_UpBound);
%获取区间长度len([a,b])=b-a;
step_length = x_UpBound - x_LowBound;
%计算第一次的复合梯度积分值
T_result(1) = step_length*(f_0 + f_1)/2;
%初始化count值值
count = 1;
%循环计算,直到精度达到要求
while 1
%步长减半
step_length = step_length/2;
%重置新增节点函数值之和
sum_new_value = 0;
%区间个数
TwoPowerCount = 2.^count;
%累加新增的节点函数值之和
% | |
% | | | 新增节点为:a+(b-a)/2
% | | | | | 新增节点为:a+(b-a)*1/4, a+(b-a)*3/4
% | | | | | | | | | 新增节点为:a+(b-a)*1/8, a+(b-a)*3/8, a+(b-a)*5/8,a+(b-a)*7/8
up_Bound = TwoPowerCount-1;
% 计算新插入节点对应的函数值之和
for j = 1:2:up_Bound
sum_new_value = sum_new_value + CalcuFunctionValue(x_LowBound + step_length*j);
end
% 计算cout次二分得到复化梯形求积结果
% 此处的T_result为不定长一维数组
T_result(count+1) = T_result(count)/2 + step_length*sum_new_value;
% 判断精度是否满足要求,如果满足,则跳出循环;否则继续二分
if abs(T_result(count+1)-T_result(count)) < accuracyValue
break;
else
count = count + 1;
end
end
result = T_result;
end四、测试结果
测试代码 :
result = AdaptiveStepIntegral(0,1,0.0000001)测试结果:
| 二分次数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 求积结果 | 0.920735492403948 | 0.939793284806177 | 0.944513521665390 | 0.945690863582701 | 0.945985029934386 | 0.946058560962768 |
| 二分次数 | 6 | 7 | 8 | 9 | 10 | |
| 求积结果 | 0.946076943060063 | 0.946081538543152 | 0.946082687411347 | 0.946082974628235 | 0.946083046432447 |
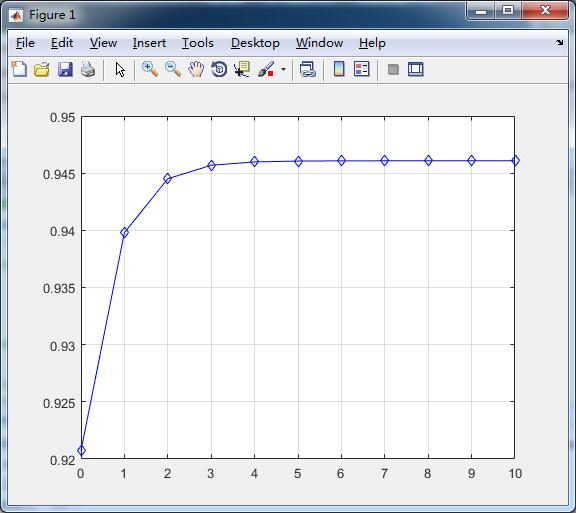
示例图:






















 1206
1206

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








