正定矩阵、正定矩阵与极值的关系、黑塞矩阵、牛顿法

目录

正定矩阵

正定矩阵与极值的关系

黑塞矩阵（Hessian Matrix）

牛顿法

---

 

正定矩阵

（1）广义定义：设A是n阶方阵，如果对任何非零向量X，都有，其中 表示X的转置，就称A为正定矩阵。

正定矩阵有以下性质  ：

（1）正定矩阵的行列式恒为正；

（2）实对称矩阵A正定当且仅当A与单位矩阵合同；

（3）若A是正定矩阵，则A的逆矩阵也是正定矩阵；

（4）两个正定矩阵的和是正定矩阵；

（5）正实数与正定矩阵的乘积是正定矩阵。

充要条件：

正定矩阵与极值的关系

判断结论同上。

 

黑塞矩阵（Hessian Matrix）

黑塞矩阵是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。黑塞矩阵产生于多元函数极值问题的判定方法。

定义：

设n元函数f(x1，x2，…… xn)有连续一阶和二阶偏导数，且在点M(xi)(i=1,2,……n；xi为已知）处梯度等于0，即 grad f(M)=0，M为驻点，由f(x1，x2，…… xn)在此点的偏导数所组成的n阶矩阵(方阵)称为黑塞矩阵(Hessian Matrix)，记为H(M)。

，其中i表示微分算子。

                                             

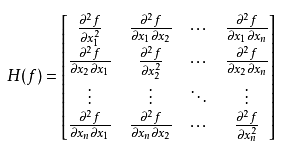
性质：

牛顿法

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(y)=0的根

牛顿法主要应用在两个方面, 1, 求方程的根; 2, 最优化。

(原文很清晰直接拿过来了：https://blog.csdn.net/batuwuhanpei/article/details/51979831)

1、求函数的根

2、最优化问题

对于最优化问题，其极值点处有一个特性就是在极值点处函数的一阶导数为0。因此我们可以在一阶导数处利用牛顿法通过迭代的方式来求得最优解，即相当于求一阶导数对应函数的根。 

这样我们就得到了一个不断更新迭代求得最优解的方法。这个也很好理解，假设我们上面的第一张图的曲线表示的是函数一阶导数的曲线，那么其二阶导数就是一阶导数对应函数在某点的斜率，也就是那条切线的斜率，那么该公式就和上面求根的公式本质是一样的。 我们这里讨论的都是在低维度的情形下，那么对于高维函数，其二阶导数就变为了一个黑塞矩阵，记为，那么迭代公式就变为了

 

这里的推导过程很直观，看看多理解：

                                                 https://blog.csdn.net/wenzishou/article/details/73350591

                                                 https://blog.csdn.net/zhangbo_0323/article/details/77779198