位姿估计 | 目标体坐标系相对于相机坐标系的位姿估计及其Python代码

引言

本文接着分享空间目标位姿跟踪和滤波算法中用到的一些常用内容，希望为后来者减少一些基础性内容的工作时间。以往分享总结见文章：位姿跟踪 | 相关内容目录和链接总结（不断更新中~~~）

本文介绍如何利用特征点求解目标体坐标系相对于相机坐标系的位姿。

技术流程

1. PNP介绍

PnP（Perspective-n-Point）是根据图像中特征点的二维像素坐标及其对应的三维空间坐标，来估计相机在参考坐标系中位姿的一类算法。

直观来讲，当相机观察到空间中的某一物体时，我们已经知道了该物体在某一参考坐标系下的位置和姿态，那么如何通过图片中物体的成像判断出相机此时在参考坐标系下的位姿？

这正是PnP要解决的问题，即利用已知三维结构与图像的对应关系求解相机与参考坐标系的相对关系（相机的外参）。

总的来说，PNP问题求解的是相机相对于参考坐标系的位姿。需要已知特征点像素坐标，以及对应的参考坐标系下的坐标值。

一般来说，利用特征点的像素坐标，以及已知的相机内参，可以获取特征点在相机坐标系下的坐标。

在已知特征点在相机坐标系下的坐标和参考坐标系下的坐标位置后，利用ICP方法可以求解相机坐标系和参考坐标系之间的相对位姿！！

2. ICP介绍

迭代最近点算法ICP （ Iterative Closest Point）：已知三维点在两个坐标系中的坐标，求这两个坐标系的变换关系，称为 ICP 问题。

ICP 算法的目的是要找到特征点匹配之间的旋转参数$R$和平移参数$T$，使得两点数据之间满足某种度量准则下的最优匹配。

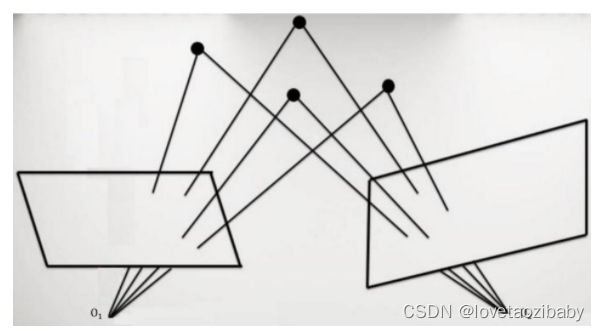
设参考坐标系下特征点坐标集合为$S_1$，相机坐标系下特征点坐标集合为$S_2$，$P_i$和$Q_i$ （又可记作$p_1^i$和$p_2^i$）分别表示特征点集$S_1$和$S_2$中某个特征点坐标。

构造目标函数：

利用SVD分解求解ICP问题，具体步骤为：

1. 首先计算特征点集的均值以及去中心点化的点坐标：
   
2. 定义矩阵$M$：
   
3. 对$M$进行奇异值分解：
   
4. 计算旋转矩阵$R$的最优解为：
   
5. 计算平移矩阵$T$：
   

ICP问题的应用包括两种：利用ICP求解相对位姿，利用ICP求解相机帧间运动。

a. 利用ICP求解目标相对相机的位姿

已知量：特征点坐标 在相机坐标系和目标坐标系下的坐标值

步骤：奇异值分解（SVD），具体求解流程见上文。

输出：目标坐标系相对于参考坐标系的旋转矩阵$R$和平移矩阵$T$，即为求解目标相对位姿。

该方法适用于求解空间目标相对于相机坐标系的位姿，在基于特征的目标位姿估计方法中比较适用。

b. 利用ICP求解相机帧间运动

ICP算法还可以根据前后两帧图像中匹配好的特征点在相机坐标系下的三维坐标，求解相机帧间运动。

直观来讲，当相机在某处观察某一物体时，我们知道了相机此时与物体之间的相对位姿关系；当相机运动到另一处，我们亦知道此时相机与物体的相对位姿关系。

已知量： $t_1$时刻相机与目标之间的相对位姿，$t_2$时刻相机与目标之间的相对位姿。

步骤：奇异值分解（SVD） 或者 非线性迭代等，具体求解流程见上文。

输出：ICP问题可以求解这两次相机与物体的相对位姿关系，从而确定相机发生了怎样的运动。

参考网址：

1. ICP 问题之 SVD
2. 视觉SLAM中的对极约束、三角测量、PnP、ICP问题

Python代码

功能：已知特征点在相机坐标系和目标坐标系的位置，利用SVD线性求解目标坐标系相对于相机坐标系的位姿，也即目标的相对位姿。（ICP问题）

import numpy as np
import math

def objpose(P, Q):
    n = P.shape[1]

    # 计算P' 和 Q' 的值
    P1 = P.copy()
    Q1 = Q.copy()
    pbar = sum(P.T)/n
    qbar = sum(Q.T)/n
    P = P - pbar.reshape((3,1))
    Q = Q - qbar.reshape((3,1))

    # SVD分解
    # 计算M矩阵
    M = np.zeros((3,3))
    for i in range(n):
        M += np.dot(P[:,i].reshape((3,1)), Q[:,i].reshape((3,1)).T)

    [U,S,V] = np.linalg.svd(M)

    # 计算旋转矩阵R
    R = np.dot(V, U.T)

    # 得到R值后， 计算t值
    Sum = np.dot(R, P1[:, 1])

    t = Q1[:, 1] - Sum

    # 方向判断
    if t[2] < 0:
        R = -R
        t = -t

    return R, t


if __name__ == '__main__':

    P = np.array([[-2,0,0],[-2,2,0],[2,0,0],[2,2,0]]).T # 3D point
    Q = np.array([[-2,0,2],[-2,2,2],[2,0,2],[2,2,2]]).T# 3D point

    [R, t] = objpose(P,Q)
    print(R)
    print(t)