【机器学习】逻辑回归

逻辑回归

分类问题

在分类问题中，我们尝试预测的是结果是否属于某一个类（例如正确或错误）。分类问题的例子有：判断一封电子邮件是否是垃圾邮件；判断一次金融交易是否是欺诈；之前我们也谈到了肿瘤分类问题的例子，区别一个肿瘤是恶性的还是良性的。

我们从二元的分类问题开始讨论。

我们将因变量(dependent variable)可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量$y\in 0,1$，其中 0 表示负向类，1 表示正向类。

我们接下来看逻辑回归，这个算法的性质是：它的输出值永远在0到 1 之间

一、基本原理

0. decision stump

公式：$f(x)=w^T-t$, if $f(x)>0$ then $\hat{y}=1$ else $\hat{y}=0$

1. 假设函数

我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。

如下图所示，其中: X 代表特征向量; f代表逻辑函数（logistic function) 是一个常用的逻辑函数为S形函数(Sigmoid function): $f(x)=\frac{1}{1+e^{-(w^{T}x-t)}}$

我们得到逻辑回归模型的假设函数f(x)的作用是：对于给定的输入变量，根据选择的参数计算输出变量=1的可能性(estimated probablity)。 例如，如果对于给定的x，通过已经确定的参数计算得出f(x)=0.7，则表示有70%的几率y为正向类，相应地y为负向类的几率为1-0.7=0.3。

判断条件： if $f(x)>0.5$ then $\hat{y}=1$ else $\hat{y}=0$

2. 判定边界

假设我们有个模型:并且参数θ 是向量[-3 1 1]。 则当-3+x1+x2 >= 0，即x1+x2 >= 3时，模型将预测 y=1。 我们可以绘制直线x1+x2=3，这条线便是我们模型的分界线，将预测为1的区域和预测为 0的区域分隔开。

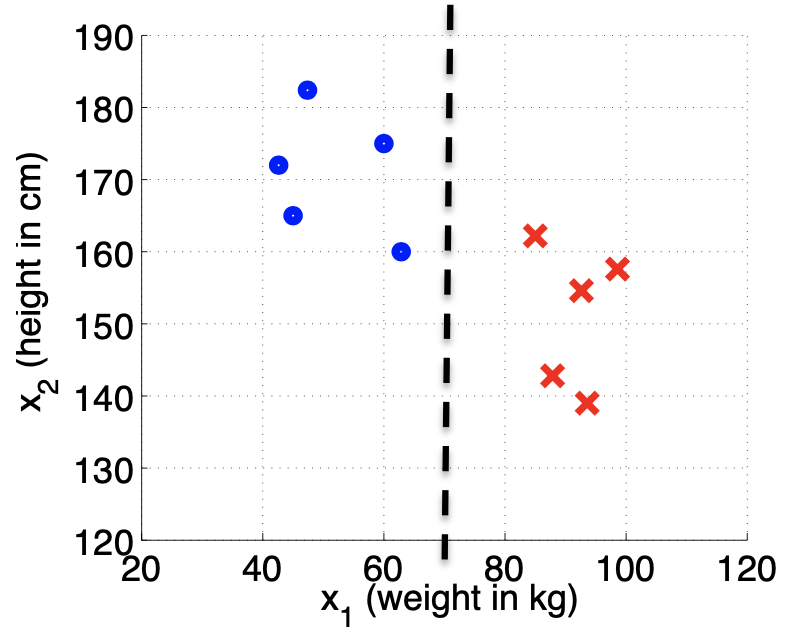
x1+x2=3 则称为下决策边界(decision boundary), 我们可以用非常复杂的模型来适应非常复杂形状的判定边界。

3. 代价函数

问题: 如何拟合逻辑回归模型的参数θ

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将f(x)带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数

这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。我们重新定义逻辑回归的代价函数，则可得到f(x)与 Cost(f(x),y)之间的关系：

$$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^{m}Cost\left(f\left(x^{\left(i\right)}\right),y^{\left(i\right)}\right)$$

$$L(f(x),y)=\{\begin{array}{ll}-log(f(x))& \text{if y=1}\\ -log(1-f(x))& \text{if y=0}\end{array}$$

即 − { y log ⁡ f ( x ) + ( 1 − y ) log ⁡ ( 1 − f ( x ) ) } - \lbrace{ y\log f(x) + (1-y)\log(1-f(x))\rbrace} −{ylogf(x)+(1−y)log(1−f(x))}

如下图所示:

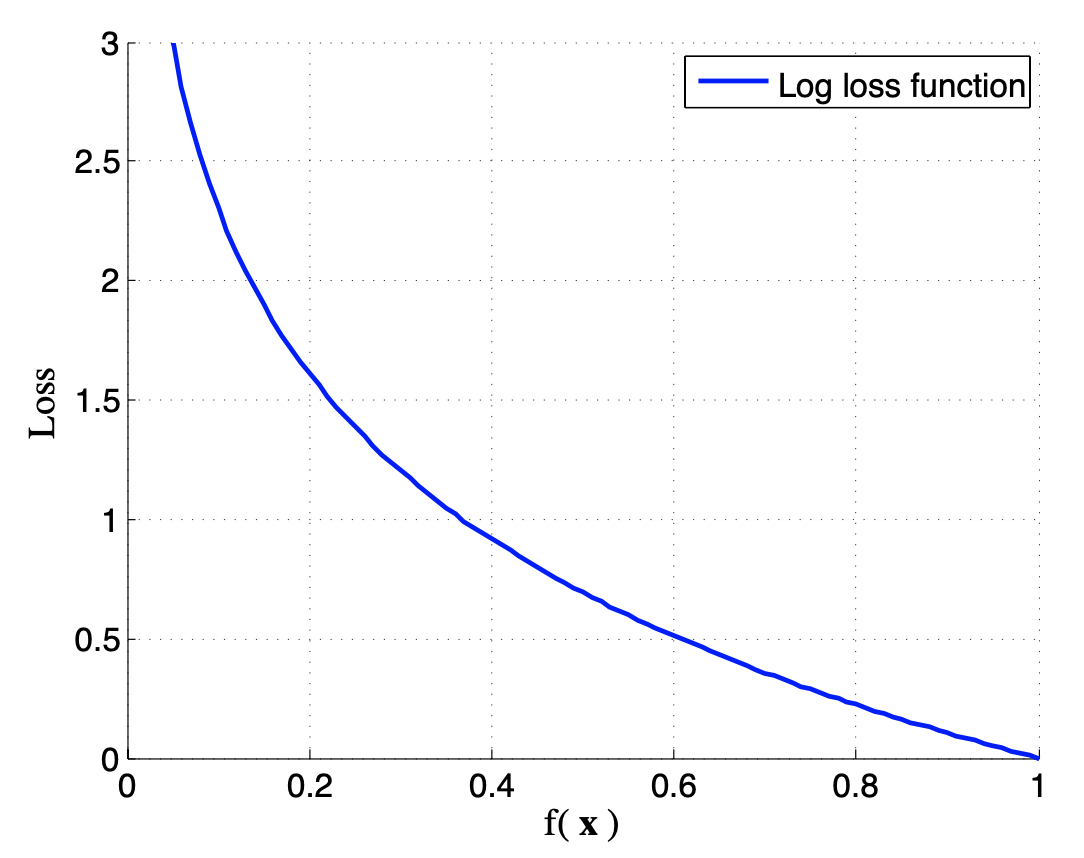
Error function(the cross entropy error): E = − ∑ i = 1 N { y log ⁡ f ( x ) + ( 1 − y ) log ⁡ ( 1 − f ( x ) ) } E = - \sum_{i=1}^N\lbrace{ y\log f(x) + (1-y)\log(1-f(x))\rbrace} E=−∑i=1N​{ylogf(x)+(1−y)log(1−f(x))}

这样就可以用梯度下降算法来求得能使代价函数最小的参数了:

${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)x_j^{(i)}$

推导结果如下所示: 虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里的h(x)与线性回归中不同，所以实际上是不一样的。

$J\left(\theta \right)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log \left(f\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-f\left(x^{(i)}\right)\right)]=\frac{1}{m}\sum _{i=1}^m[f\left(x^{(i)}\right)-y^{(i)}]x_j^{(i)}$

伪代码: $\frac{\partial E}{\partial w_j}={\sum }_i(f(x_i)-y_i)\cdot x_{ij}$

w ← randvector(), α ← 0.1 
repeat
	for each parameter j do 
    	wj = wj − α(∂E/∂wj)	# move wj in direction of negative gradient
	end for 
until termination criterion met

二、代码实现

1.SKLearn

LogisticRegression

# 导入模块
from sklearn.linear_model import LogisticRegression
import numpy as np
from sklearn.datasets import load_breast_cancer

# 导入数据集
breast_cancer = load_breast_cancer()
data_X = breast_cancer.data
data_y = breast_cancer.target

# 设置逻辑回归模块
model = LogisticRegression(solver='lbfgs', max_iter = 10000)
# 训练数据, 得出参数
model.fit(data_X, data_y)

# 分数
print(model.score(data_X, data_y))

SGDClassifier

可以对学习速率进行修改

model = SGDClassifier(loss="log", learning_rate='constant', eta0=eta)

2. 实现

代价函数

def h(theta,X):
    return expit(np.dot(X,theta))

def computeCost(theta,X,y):
    m = y.size

    hypothesis = h(theta, X)
    cost = np.sum(np.dot((-1 * y).T, np.log(hypothesis))
                  - np.dot((1 - y).T, np.log(1 - hypothesis))) / m
    grad = np.dot(X.T, (hypothesis - y)) / m

    return cost

边界

def optimizeTheta(mytheta,myX,myy, maxiter):
    result = optimize.fmin(computeCost, x0=mytheta, args=(myX, myy), maxiter=maxiter, full_output=True)
    return result[0], result[1]

def Boundary(initial_theta, X, y, maxiter):
    theta, mincost = optimizeTheta(initial_theta, X, y, maxiter)
    # print(theta)
    # boundary_xs = np.array([np.min(X[:, 1]), np.max(X[:, 1])])
    # boundary_ys = (-1. / theta[2]) * (theta[0] + theta[1] * boundary_xs)
    return theta, mincost