【机器学习】关联规则与FP-Tree

FP-Tree算法

　　FP-Tree算法只需要遍历一次事务，然后可以建立FP-Tree树形数据结构来表征事务项目出现的关系。FP-Tree相比原始事务，将各个事务压缩到一个树，保存了项目之间的关系和出现频数，但是规模小得多。我可以直接根据FP-Tree来获取所有事务项目集合出现的次数。
　　下面是初始化步骤：
　　1、事务项目排序。假设我获取了事务T，首先计算每个事务项目出现的次数，把单个事务项目次数少于阈值的事务项目去掉，因为这些事务项目的父集合一定不是频繁集。剩下的事务项目都是1元频繁集，按照出现次数降序列表，称为F1。设F1表为：A,B,C,D
　　2、根据F1的顺序,重新对每个事务进行排序。设某条事务为：C,D,A，则重排序为A,C,D。
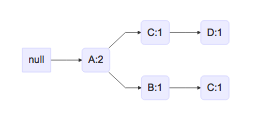
　　3、每个排好序的事务都是一条路径，我可以根据路径构建一棵树，书的根节点设为NULL。如项目事务为ACD,ABC,BC，那么可以构建树，树节点冒号跟着出现次数：
　　
　　FP-Tree算法从这里开始进入递归步骤，算法为(http://www.cnblogs.com/zhangchaoyang/articles/2198946.html)：
　　

输入:事务集合 List<List<String>> transactions
输出:频繁模式集合及相应的频数 Map<List<String>,Integer> FrequentPattens

初始化 PostModel=[],CPB=transactions
void FPGrowth(List<List<String>> CPB,List<String> PostModel){
    if CPB为空：
        return

    统计CPB中每一个项目的计数，把计数小于最小支持数minSuport的删除掉，对于CPB中的每一条事务按项目计数降序排列。
    由CPB构建FP-Tree，FP-Tree中包含了表头项headers，每一个header都指向了一个链表HeaderLinkList，链表中的每个元素都是FP-Tree上的一个节点，且节点名称与header.name相同。
    for header in headers:
        newPostModel=header.name+PostModel
        把<newPostModel, header.count>加到FrequentPattens中。
        newCPB=[]
        for TreeNode in HeaderLinkList:
            得到从FP-Tree的根节点到TreeNode的全路径path，把path作为一个事务添加到newCPB中，要重复添加TreeNode.count次。
        FPGrowth(newCPB,newPostModel)

　　　假设当前已知频繁集B，我要找包含B且为频繁集的父频繁集，需要找到从根节点到B的所有路径来构建一个新的FP-Tree。B就是postmodel后缀模式，简写为PM；根节点到B的所有路径的集合就是CPB条件模式基。CPB中可能有重复的路径，或者不同路径有重复部分，迭代过程中按照上面的方法，用CPB来构建包含支持度信息的FP-Tree。FP-Tree中单根分叉的子节点的支持度，一定小于等于父节点的支持度；不过子节点总的支持度，可能比该子节点的某个父节点要多（情况二）。这是对事务进行排序后获得的有序结果。假设支持度阈值为最少出现3次。
　　上述迭代函数FPGrowth，第一步的输入，CPB是原始的、排除了1元非频繁集的事务路径，PM是空，写作NULL，可以认为根节点到NULL的路径是所有的初始化事务路径；header表头项理所当然是就是F1表。第一步我遍历F1表，表上的项目已经满足支持度条件了，因此我将NULL和这些项目组合，这样就找出了所有的1元频繁集。然后遍历这些1元频繁集，倒序依次取表头项Headers的元素X作为newPM，找到当前FP-Tree中根节点到X的所有路径作为newCPB，进行下一次关于X的迭代FPGrowth；关于X的搜索完成后，再回来进行X上一个元素W的搜索。整个过程类似深度搜索。
　　假设D频繁集（含有N个元素，N>0）为PM，已知CPB，那么我重新构建FP-Tree，以及一个新的表头项Headers，Headers保存当前FP-Tree中存在的元素的总出现次数。次数少于支持度阈值的节点可以预先排除。我画出情况（1）：
　　
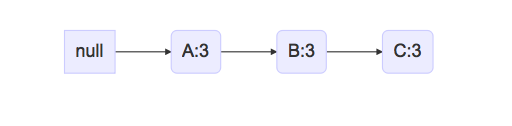
　　由于我的CPB是根节点到D的所有路径，如果FP-Tree中只有一条路径，那么这条路径上的节点，都可以到D三次，彼此之间也都可以共存3次，ABC任意组合都满足支持度阈值。因此ABC可以任意组合，然后末尾加上D后缀模式组成频繁集，出现次数为3，加入置信度计算队列中，关于D的搜索结束。注意真实事务中，如A->B的路径可能大于3，多出来的路径是不会到D，我构建D的CPB时，多余的路径被排除了；这一轮分析中，只能得出包含D的频繁集以及频数，比如A->B的实际路径频数可能大于3，虽然我可以认定AB是频繁集，但是不能获得该频繁集的真实频数，必须在之后的迭代中才能计算得到。
　　如果新FP-Tree有多条路径，那么我必须用Headers表头统一分析，不能沿着树的分叉进行分析。我画出情况二：
　　
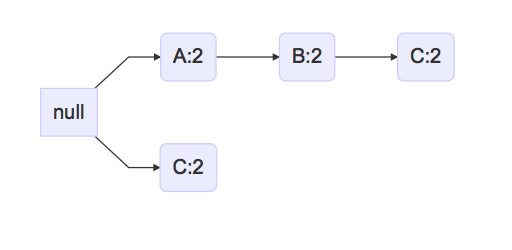
　　可以看出，第一条和第二条路径中项目的支持度都为2，但是CD是频繁集。如果单纯分析每个分叉，那么会得出没有频繁集的错误结论。这时候我需要使用刚刚建立的新表头项Headers：
　　A:2 B:2 C:4 (D:4)
　　根据表头项，C的支持度为4，即后缀模式D可以和C组合成为支持度为4的频繁集，然后作为新的后缀模式CD。在下一轮迭代中，新CPB的第一条路径的节点（A:2->B:2）的支持度不满足条件，第二条路径为空，包含D的频繁集搜索完毕。
　　现在我来看看这个迭代过程是否能完全搜索所有的频繁集。在一次FP-Tree迭代中，我们的搜索从Header表头中支持度低的事务项目开始，这样就可以保证搜索的有序。新FP-Tree的构建严格遵循第一次构建FP-Tree时的表头Header的各个事务项目的顺序，表头中排序靠后的事务项目，在树的单根分叉中永远不可能出现在排序靠前的事务项目的前面。这样，假设事务项目有ABCD，从D开始迭代搜索，可以扫描包含D的所有候选频繁集；从C开始搜索，会扫描包含C且不包含D的候选频繁集，这样就不会重复。经过迭代搜索后，所有可能的候选频繁集都会被扫描到。