形象解释Transformer中的自注意力机制

lpy0204

已于 2024-10-11 15:49:03 修改

阅读量994

点赞数 25

文章标签： transformer 深度学习人工智能

于 2024-10-10 12:37:50 首次发布

本文链接：https://blog.csdn.net/lpy0204/article/details/142787433

版权

我们以下面这句话为例子来说明一下Transformer中的自注意力机制：

我是小狗

一、将token嵌入

首先要将每一个字（token）嵌入为一个向量，这里可以采用one-hot编码等。假设每个嵌入向量的维度都为512维。我们将“我”表示为 $vec_{0}\in \mathbb{R}^{1\times 512}$ ，“是”嵌入的向量表示为 $vec_{1}\in \mathbb{R}^{1\times 512}$ ...那么由所有嵌入向量组成的嵌入矩阵就为：

$\begin{bmatrix} vec_{0} \\ vec_{1}\\vec_{2}\\vec_{3}\end{bmatrix}_{4\times 512}$

将该嵌入矩阵（Input Embedding）加上位置编码就得到了输入矩阵，将该矩阵记作 $W_{in}$ ，表示为：

$\begin{bmatrix} vec_{0}^{'} \\ vec_{1}^{'}\\vec_{2}^{'}\\vec_{3}^{'}\\\end{bmatrix}_{4\times 512}$

二、生成Q、K、V向量

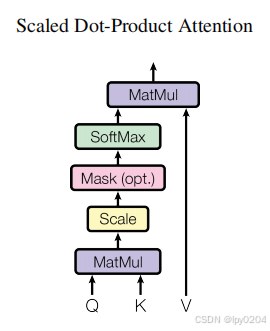
我们首先随机生成三个矩阵 $W_{Q}\in \mathbb{R}^{512\times d_{k}}$ ， $W_{K}\in \mathbb{R}^{512\times d_{k}}$ ， $W_{V}\in \mathbb{R}^{512\times d_{v}}$ ，意为Query、Key以及value，他们的第一维度一定都为512维（要与 $W_{in}$ 相乘），我们假设它的第二维度都是64维，即 $d_{k}=d_{v}=64$ （与原始论文一致）。它们的作用相当于神经网络中各层的权重，是要逐渐地被训练的。将 $W_{in}$ 和以上三个矩阵分别相乘得到了Q、K、V三个矩阵，即最上面图片中的"Scaled Dot-Product Attention"中的三个输入。

$Q=\begin{bmatrix} vec_{0}^{'} \\ vec_{1}^{'}\\vec_{2}^{'}\\vec_{3}^{'}\end{bmatrix}_{4\times 512}\cdot \left [ W_{q} \right ]_{512\times 64}= \begin{bmatrix} vec_{0}^{'}\cdot W_{q} \\ vec_{1}^{'}\cdot W_{q}\\vec_{2}^{'}\cdot W_{q}\\vec_{3}^{'}\cdot W_{q}\\\end{bmatrix}_{4\times 64}=\begin{bmatrix} Q_{0} \\ Q_{1}\\Q_{2}\\Q_{3}\end{bmatrix}_{4\times 64}$

其中 $Q_{0}$ 是"我"的Query向量， $Q_{1}$ 是"是"的Query向量......

$K=\begin{bmatrix} vec_{0}^{'} \\ vec_{1}^{'}\\vec_{2}^{'}\\vec_{3}^{'}\end{bmatrix}_{4\times 512}\cdot \left [ W_{k} \right ]_{512\times 64}= \begin{bmatrix} vec_{0}^{'}\cdot W_{k} \\ vec_{1}^{'}\cdot W_{k}\\vec_{2}^{'}\cdot W_{k}\\vec_{3}^{'}\cdot W_{k}\\\end{bmatrix}_{4\times 64}=\begin{bmatrix} K_{0} \\ K_{1}\\K_{2}\\K_{3}\end{bmatrix}_{4\times 64}$

$V=\begin{bmatrix} vec_{0}^{'} \\ vec_{1}^{'}\\vec_{2}^{'}\\vec_{3}^{'}\end{bmatrix}_{4\times 512}\cdot \left [ W_{v} \right ]_{512\times 64}= \begin{bmatrix} vec_{0}^{'}\cdot W_{v} \\ vec_{1}^{'}\cdot W_{v}\\vec_{2}^{'}\cdot W_{v}\\vec_{3}^{'}\cdot W_{v}\end{bmatrix}_{4\times 64}=\begin{bmatrix} V_{0} \\ V_{1}\\V_{2}\\V_{3}\end{bmatrix}_{4\times 64}$

三、MatMul

然后将Q和K的转置相乘：

$Q\cdot K^{T}=\begin{bmatrix} Q_{0} \\ Q_{1}\\Q_{2}\\Q_{3}\end{bmatrix}_{4\times 64} \cdot \begin{bmatrix} K_{0} &K_{1}&K_{2}&K_{3}\end{bmatrix}_{64\times 4}$

$=\begin{bmatrix} Q_{0} \cdot K_{0} & Q_{0} \cdot K_{1} &Q_{0} \cdot K_{2} & Q_{0} \cdot K_{3} \\ Q_{1}\cdot K_{0} & Q_{1}\cdot K_{1} & Q_{1}\cdot K_{2} &Q_{1}\cdot K_{3} \\Q_{2}\cdot K_{0} & Q_{2}\cdot K_{1} &Q_{2}\cdot K_{2}&Q_{2}\cdot K_{3} \\Q_{3}\cdot K_{0} & Q_{3}\cdot K_{1} &Q_{3}\cdot K_{2}&Q_{3}\cdot K_{3}\end{bmatrix}_{4\times 4}$

我们知道 $Q_{i}\cdot K_{j}$ 相当于是 $Q_{i}$ 在 $K_{j}$ 上的投影，投影数值的大小反映了 $token_{i}$ 对 $token_{j}$ 的注意力大小。在该矩阵中第 $i$ 行反映了 $token_{i}$ 对其他 $token$ 的注意力大小（包括自己）。

四、Scale

这一步就是简单地将 $Q\cdot K^{T}$ 的值除以 $\sqrt{d_{k}}$ （原论文中采用的），这样做的目的是防止向量内积过大（因为这些大数值在缩放后要通过softmax函数，由于softmax函数的性质，它会放大数值差异，导致数值稳定性问题。在反向传播时，这可能会导致梯度消失或爆炸）。

$\frac{Q\cdot K^{T}}{\sqrt{d_{k}}}=\frac{1}{8}\begin{bmatrix} Q_{0} \cdot K_{0} & Q_{0} \cdot K_{1} &Q_{0} \cdot K_{2} & Q_{0} \cdot K_{3} \\ Q_{1}\cdot K_{0} & Q_{1}\cdot K_{1} & Q_{1}\cdot K_{2} &Q_{1}\cdot K_{3} \\Q_{2}\cdot K_{0} & Q_{2}\cdot K_{1} &Q_{2}\cdot K_{2}&Q_{2}\cdot K_{3} \\Q_{3}\cdot K_{0} & Q_{3}\cdot K_{1} &Q_{3}\cdot K_{2}&Q_{3}\cdot K_{3}\end{bmatrix}_{4\times 4}$

五、Mask(可选)

从前面的推导可以得知，Transformer会同时计算每一个token对其他所有token的注意力。但是当我们进行预测时，我们是不能看到（注意到）当前token往后的所有token的，所以不能计算当前token对后面的token的注意力。方法就是将 $\frac{Q\cdot K^{T}}{\sqrt{d_{k}}}$ 中的上三角区域（除去主对角线）全部变为-inf，这样在进行softmax后值为-inf的部分就全部变为0。

$Masked (\frac{Q\cdot K^{T}}{\sqrt{d_{k}}})=\frac{1}{8}\begin{bmatrix} Q_{0} \cdot K_{0} & -inf & -inf & -inf \\ Q_{1}\cdot K_{0} & Q_{1}\cdot K_{1} & -inf & -inf \\Q_{2}\cdot K_{0} & Q_{2}\cdot K_{1} &Q_{2}\cdot K_{2}& -inf\\Q_{3}\cdot K_{0} & Q_{3}\cdot K_{1} &Q_{3}\cdot K_{2}&Q_{3}\cdot K_{3}\end{bmatrix}_{4\times 4}$

六、Softmax

用softmax将每一行转换为一个概率分布，每行中的所有元素和为1。

$Softmax(\frac{Q\cdot K^{T}}{\sqrt{d_{k}}})=\begin{bmatrix} \frac{e^{Q_{0}\cdot K_{0}}}{\sum\limits^{i=3}_{i=0}e^{Q_{0}\cdot K_{i}}}&\frac{e^{Q_{0}\cdot K_{1}}}{\sum\limits^{i=3}_{i=0}e^{Q_{0}\cdot K_{i}}}&\frac{e^{Q_{0}\cdot K_{2}}}{\sum\limits^{i=3}_{i=0}e^{Q_{0}\cdot K_{i}}}&\frac{e^{Q_{0}\cdot K_{3}}}{\sum\limits^{i=3}_{i=0}e^{Q_{0}\cdot K_{i}}} \\ \frac{e^{Q_{1}\cdot K_{0}}}{\sum\limits^{i=3}_{i=0}e^{Q_{1}\cdot K_{i}}}&\frac{e^{Q_{1}\cdot K_{1}}}{\sum\limits^{i=3}_{i=0}e^{Q_{1}\cdot K_{i}}}&\frac{e^{Q_{1}\cdot K_{2}}}{\sum\limits^{i=3}_{i=0}e^{Q_{1}\cdot K_{i}}}&\frac{e^{Q_{1}\cdot K_{3}}}{\sum\limits^{i=3}_{i=0}e^{Q_{1}\cdot K_{i}}}\\\ \frac{e^{Q_{2}\cdot K_{0}}}{\sum\limits^{i=3}_{i=0}e^{Q_{2}\cdot K_{i}}}&\frac{e^{Q_{2}\cdot K_{1}}}{\sum\limits^{i=3}_{i=0}e^{Q_{2}\cdot K_{i}}}&\frac{e^{Q_{2}\cdot K_{2}}}{\sum\limits^{i=3}_{i=0}e^{Q_{2}\cdot K_{i}}}&\frac{e^{Q_{2}\cdot K_{3}}}{\sum\limits^{i=3}_{i=0}e^{Q_{2}\cdot K_{i}}}\\\frac{e^{Q_{3}\cdot K_{0}}}{\sum\limits^{i=3}_{i=0}e^{Q_{3}\cdot K_{i}}}&\frac{e^{Q_{3}\cdot K_{1}}}{\sum\limits^{i=3}_{i=0}e^{Q_{3}\cdot K_{i}}}&\frac{e^{Q_{3}\cdot K_{2}}}{\sum\limits^{i=3}_{i=0}e^{Q_{3}\cdot K_{i}}}&\frac{e^{Q_{3}\cdot K_{3}}}{\sum\limits^{i=3}_{i=0}e^{Q_{3}\cdot K_{i}}}\end{bmatrix}_{4\times 4}$ $=\begin{bmatrix} p_{00} & p_{01}&p_{02} & p_{03} \\ p_{10}& p_{11}& p_{12}&p_{13}\\p_{20}&p_{21}&p_{22}&p_{23}\\p_{30}&p_{31}&p_{32}&p_{33}\end{bmatrix}_{4\times 4}$

其中 $p_{ij}$ 表示了一个权重，即 $token_{i}$ 应该放多少比例的注意力到 $token_{j}$ 上。例如当 $\frac{Q\cdot K^{T}}{\sqrt{d_{k}}}$ 进行Mask和Softmax操作后，它的第一行会变成 $[1 \ 0\ 0\ 0]$ ，也就是说 $token_{0}$ 应该把全部注意力放在 $token_{0}$ 上，而对于其他 $token$ 则不应该关注。

七、MatMul

将这个比例再乘以value(值)矩阵 $V$ 进行点乘，得到了注意力 $Attention(Q,K,V)$ 的最终形式：

$Softmax(\frac{Q\cdot K^{T}}{\sqrt{d_{k}}})V=\begin{bmatrix} p_{00} & p_{01}&p_{02} & p_{03} \\ p_{10}& p_{11}& p_{12}&p_{13}\\p_{20}&p_{21}&p_{22}&p_{23}\\p_{30}&p_{31}&p_{32}&p_{33}\end{bmatrix}_{4\times 4}\cdot \begin{bmatrix} V_{0} \\ V_{1}\\V_{2}\\V_{3}\end{bmatrix}_{4\times 64}$

$=\begin{bmatrix} p_{00}V_{0}+p_{01}V_{1} +p_{02}V_{2}+p_{03}V_{3} \\ p_{10}V_{0}+p_{11}V_{1} +p_{12}V_{2}+p_{13}V_{3}\\p_{20}V_{0}+p_{21}V_{1} +p_{22}V_{2}+p_{23}V_{3}\\p_{30}V_{0}+p_{31}V_{1} +p_{32}V_{2}+p_{33}V_{3} \end{bmatrix}_{4\times 64}$