transformer--编码器1(掩码张量、注意力机制、多头注意力机制)

编码器部分:

• 由N个编码器层堆叠而成
• 每个编码器层由两个子层连接结构组成
• 第一个子层连接结构包括一个多头自注意力子层和规范化层以及一个残差连接。第二个子层连接结构包括一个前馈全连接子层和规范化层以及一个残差连接 

掩码张量

什么是掩码张量

掩代表遮掩，码就是我们张量中的数值，它的尺寸不定，里面一般只有1和0的元素，代表位置被遮掩或者不被遮掩，至于是0位置被遮掩还是1位置被遮掩可以自定义，因此它的作用就是让另外一个张量中的一些数值被遮掩，也可以说被替换,它的表现形式是一个张量.

掩码张量的作用:

在transformer中,掩码张量的主要作用在应用attention时，有一些生成的attention张量中的值计算有可能已知了未来信息而得到的，未来信息被看到是因为训练时会把整个输出结果都一次性进行Embedding，但是理论上解码器的的输出却不是一次就能产生最终结果的，而是一次次通过上一次结果综合得出的，因此，未来的信息可能被提前利用.所以，我们会进行遮掩.

code

from inputs import Embeddings,PositionalEncoding
import numpy as np
import torch
import matplotlib.pyplot as plt
def subsequent_mask(size):
    """
    生成向后遮掩的掩码张量，参数size是掩码张量最后两个维度的大小，
    他们最好会形成一个方阵
    """
    attn_shape = (1,size,size)
    # 使用np.ones方法向这个形状中添加1元素，形成上三角阵
    subsequent_mask = np.triu(np.ones(attn_shape),k=1).astype('uint8')

    # 最后将numpy类型转化为torch中的tensor，内部做一个1-的操作，
    # 在这个其实是做了一个三角阵的反转，subsequent_mask中的每个元素都会被1减
    # 如果是0，subsequent_mask中的该位置由0变成1
    # 如果是1，subsequent_mask中的该位置由1变成0
    return torch.from_numpy(1-subsequent_mask)

 输出效果分析:
通过观察可视化方阵,黄色是1的部分,这里代表被遮掩,紫色代表没有被遮掩的信息,横坐标代表目标词汇的位置,纵坐标代表可查看的位置;
我们看到,在0的位置我们一看望过去都是黄色的,都被遮住了，1的位置一眼望过去还是黄色,说明第一次词还没有产生,从第二个位置看过去,就能看到位置1的词,其他位置看不到,以此类推.

注意力机制

原理理解

原来参考文章1这篇文章已经把注意力机制讲解的很清晰了，我就不罗嗦了，大家仔细研读，后续更多的是代码实现，还可以多参考几篇，文章2，文章3

下面我使用上面文章1的图进行简要理解什么是注意力机制：

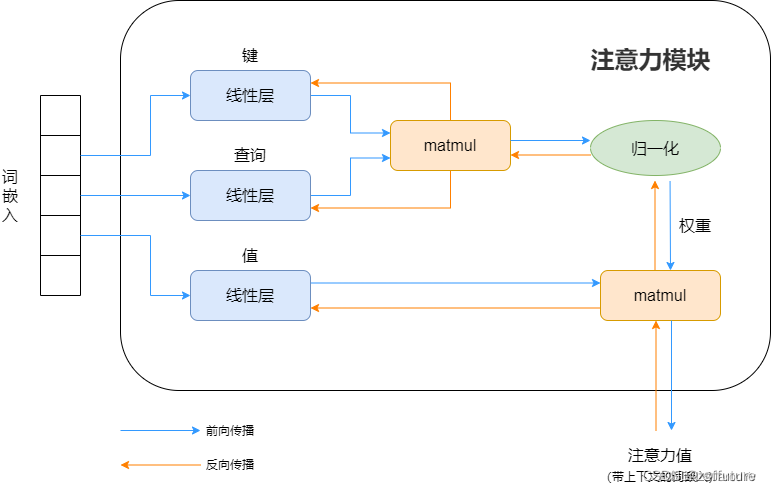
注意力说白了就是把一句话相关性的词找到，并使其更相关，弱化不相关的内容，和我们提炼一句话主要内容类似，但是如何能找到呢？现在知道的是每个词假如都是512维度的词嵌入向量构成（假如向量已经是训练好的，这个向量就是代表这个词），那么如何计算 一句话比较相关的词呢？因为每个token(词)都是一个向量表示，而向量计算相关性，直观的方法就是内积呀，所以使用内积就可以计算词与词的相关性了，虽然词宇词的相关性可以计算了，但是一句话我也不知道哪个词才是最重要的，如果不知道哪个词是重要的后续也是无法提取主要内容的，此时最直观的想法就是给词加个权重，越重要越相关，权重越大，理论上来说这个思路是可行的，但是应该怎么做呢？我现在唯一知道的就是每个词都由512维的向量构成，也知道可以计算每个词彼此之间的相似性，但是怎么加权重呢？我们可以想象数学领域的加权求和（概率论是期望），我们也可效仿，假如现在我计算第一个词和整个句子的其他词哪个最相关，最简单的做法就是把当前词的词向量和整个句子的词向量进行求内积即计算，如果和当前词的相关性很大，那计算出来的内积就会很大，同时希望权重也大，因此我们发现内积和希望的权重是正相关的，所以可以考虑直接把内积值作为权重即可，但整个权重是相对宇整个句子，权重值没有进行统一度量，因此做一个softmax就可以定性的确定比重问题。权重有了，那如何计算这个所谓的注意力呢？现在我们明确一下有哪些已知量，词嵌入向量、每个词和整个句子的其他词的权重，数学中的期望其实就相当于加权求和以此代表该物理量的平均结果，同理我们也可以求期望，这样就可以衡量当前词在所有词中的平均相关性程度，同时这个期望就是注意力值。上面的过程可以用下图表示：